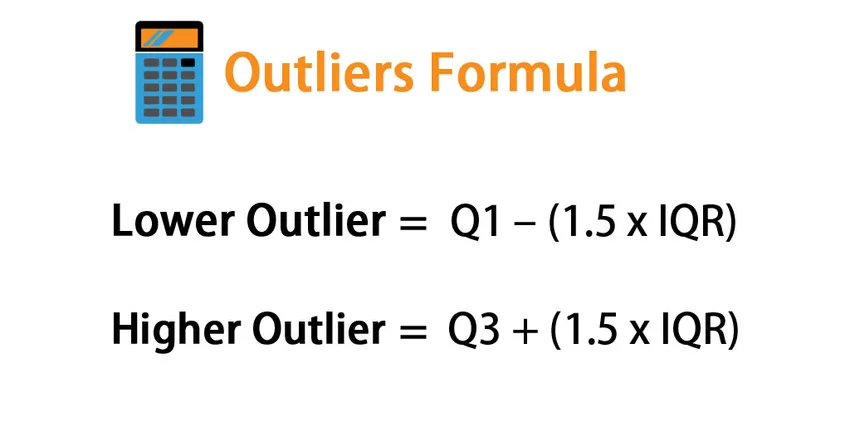
Ausreißerformel (Inhaltsverzeichnis)
- Ausreißer-Formel
- Beispiele für Ausreißerformeln (mit Excel-Vorlage)
Ausreißer-Formel
In der Statistik sind Ausreißer die beiden extrem weit auseinander liegenden ungewöhnlichen Punkte in den angegebenen Datensätzen. Die extrem hohen und extrem niedrigen Werte sind die Ausreißerwerte eines Datensatzes. Dies ist sehr nützlich, um aufgetretene Fehler zu finden. Wie der Name schon sagt, sind Ausreißer Werte, die außerhalb der übrigen Werte des Datensatzes liegen. Betrachten Sie beispielsweise Ingenieurstudenten und stellen Sie sich vor, sie hätten Zwerge in ihrer Klasse. Zwerge sind also die Menschen, die im Vergleich zu anderen normal großen Menschen extrem klein sind. Das ist also der Ausreißerwert in dieser Klasse. Ausreißerwerte können mit der Tukey-Methode berechnet werden.
Die Formel für Ausreißer -
Lower Outlier = Q1 – (1.5 * IQR)
Higher Outlier= Q3 + (1.5 * IQR)
Beispiele für Ausreißerformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung der Ausreißerformel besser zu verstehen.
Sie können diese Ausreißervorlage hier herunterladen - AusreißervorlageAusreißerformel - Beispiel # 1
Berücksichtigen Sie den folgenden Datensatz und berechnen Sie die Ausreißer für den Datensatz.
Datensatz = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23
Aufsteigende Reihenfolge des Datensatzes:
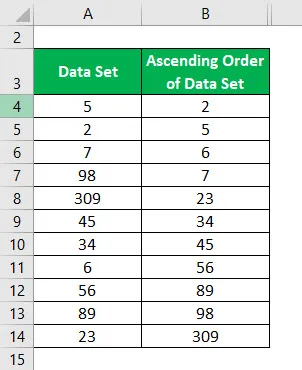
Der Median des Datensatzes der aufsteigenden Reihenfolge wird berechnet als:
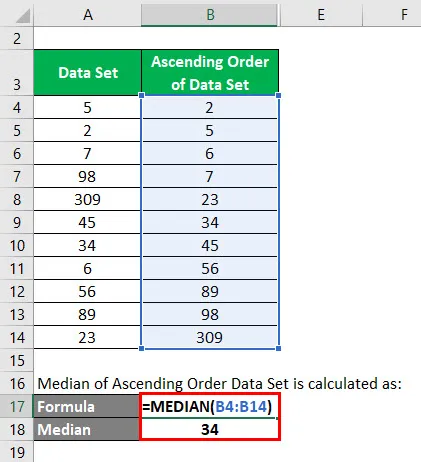
In diesem Datensatz beträgt die Gesamtzahl der Daten 11. Also n = 11. Median = 11 + 1/2 = 12/2 = 6. Daher ist der Wert, der in diesem Datensatz an sechster Stelle steht, der Median.
Also Medianwert = 34.
Teilen Sie den Datensatz mit dem Median in zwei Hälften.
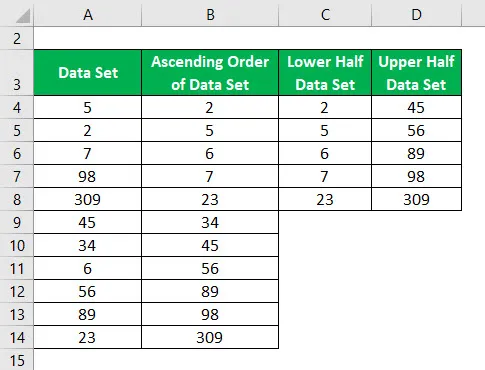
Der Median der unteren und oberen Hälfte des Datensatzes wird wie folgt berechnet:
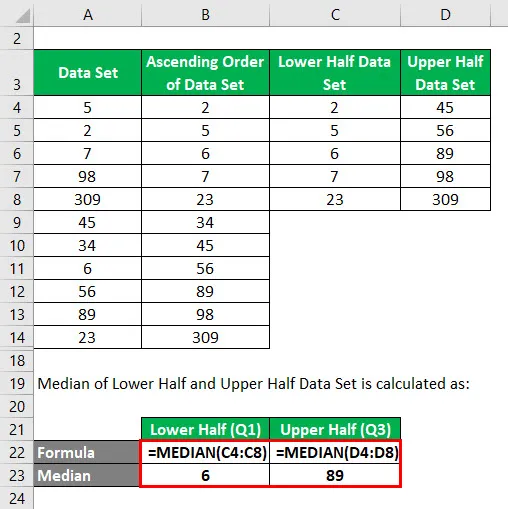
- In der unteren Hälfte 2, 5, 6, 7, 23 wäre der Medianwert 6, wenn wir den Median wie in Schritt 2 finden würden. Also ist Q1 = 6.
- In der oberen Hälfte 45, 56, 89, 98, 309 wäre der Medianwert 89, wenn wir den Median wie in Schritt 2 finden würden. Also Q3 = 89.
Der IQR wird nach der unten angegebenen Formel berechnet
IQR = Q3 - Q1
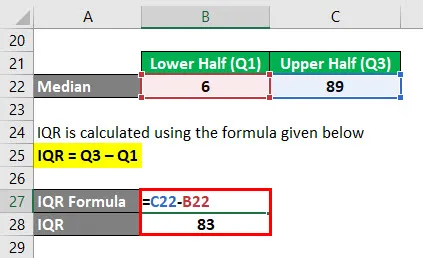
- IQR = 89 & ndash; 6
- IQR = 83
Lower Outlier wird nach der unten angegebenen Formel berechnet
Unterer Ausreißer = Q1 - (1, 5 * IQR)
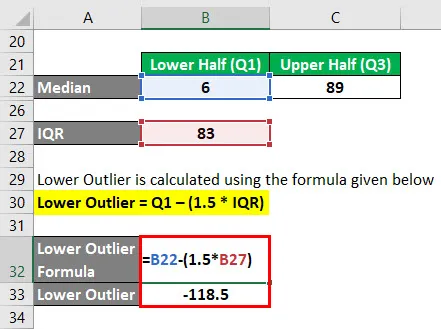
- Unterer Ausreißer = 6 - (1, 5 * 83)
- Unterer Ausreißer = -118, 5
Höherer Ausreißer wird mit der unten angegebenen Formel berechnet
Höherer Ausreißer = Q3 + (1, 5 * IQR)
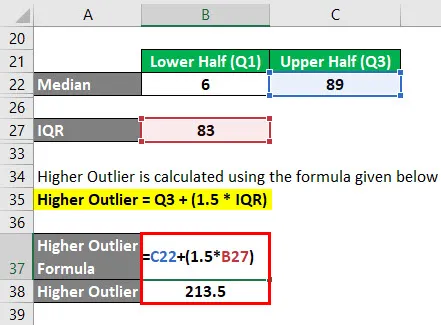
- Höherer Ausreißer = 89+ (1, 5 * 83)
- Höherer Ausreißer = 213, 5
Holen Sie sich nun diese Werte in den Datensatz -118.5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213.5, 309. Werte, die auf der unteren Seite niedriger und auf der oberen Seite höher sind sind der Ausreißerwert. Für diesen Datensatz ist 309 der Ausreißer.
Ausreißerformel - Beispiel # 2
Berücksichtigen Sie den folgenden Datensatz und berechnen Sie die Ausreißer für den Datensatz.
Datensatz = 45, 21, 34, 90, 109.
Aufsteigende Reihenfolge des Datensatzes:
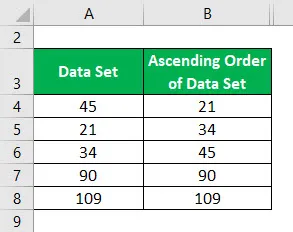
Der Median des Datensatzes der aufsteigenden Reihenfolge wird berechnet als:
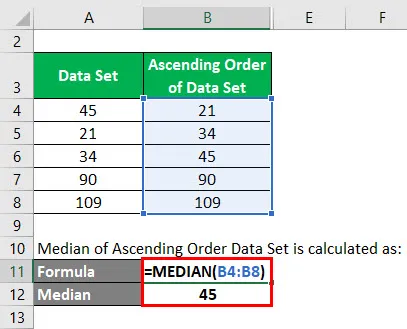
In diesem Datensatz beträgt die Gesamtzahl der Daten 5. Also n = 5. Median = 5 + 1/2 = 6/2 = 3. Daher ist der Wert, der in diesem Datensatz an dritter Stelle steht, der Median.
Also Medianwert = 45.
Teilen Sie den Datensatz mit dem Median in zwei Hälften.
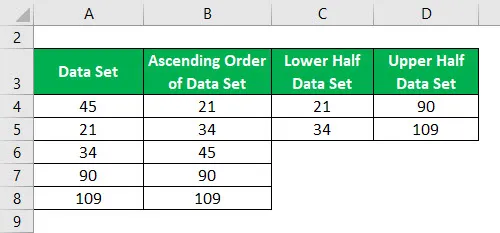
Der Median der unteren und oberen Hälfte des Datensatzes wird wie folgt berechnet:
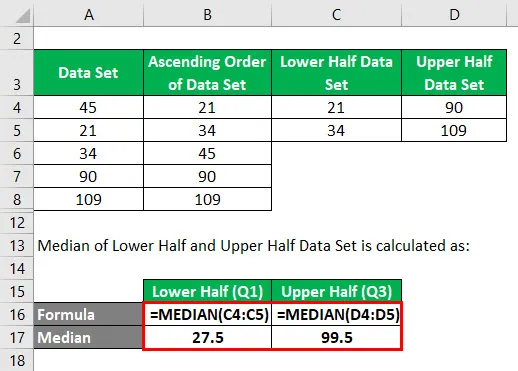
- Q1 = 27, 5
- Q3 = 89
Der IQR wird nach der unten angegebenen Formel berechnet
IQR = Q3 - Q1
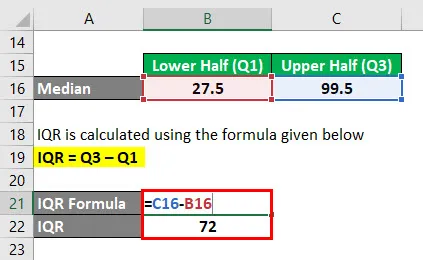
- IQR = 99, 5 - 27, 5
- IQR = 72
Lower Outlier wird nach der unten angegebenen Formel berechnet
Unterer Ausreißer = Q1 - (1, 5 * IQR)
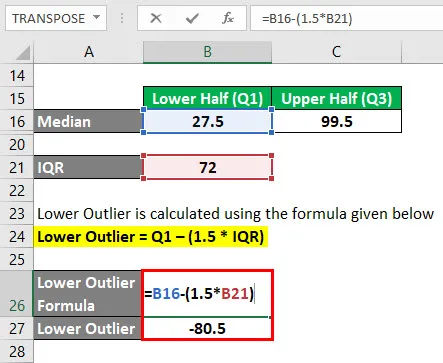
- Unterer Ausreißer = 27, 5 - (1, 5 * 72)
- Unterer Ausreißer = -80, 5
Höherer Ausreißer wird mit der unten angegebenen Formel berechnet
Höherer Ausreißer = Q3 + (1, 5 * IQR)
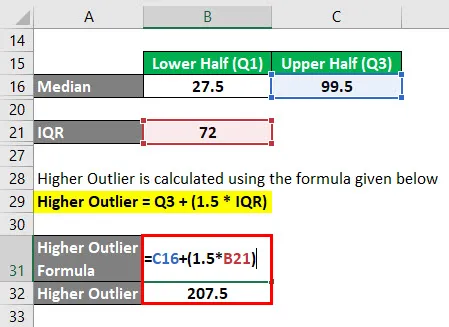
- Höherer Ausreißer = 99, 5 + (1, 5 * 72)
- Höherer Ausreißer = 207, 5
Erläuterung
Schritt 1: Ordnen Sie alle Werte im angegebenen Datensatz in aufsteigender Reihenfolge an.
Schritt 2: Finden Sie den Medianwert für die Daten, die sortiert sind. Der Median kann mit der folgenden Formel ermittelt werden. Die folgende Berechnung gibt Ihnen einfach die Position des Medianwerts an, der sich im eingestellten Datum befindet.
Median = (n + 1) / 2
Wobei n die Gesamtzahl der im Datensatz verfügbaren Daten ist.
Schritt 3: Ermitteln Sie den unteren Quartilwert Q1 aus dem Datensatz. Um dies zu ermitteln, teilen Sie den Datensatz mithilfe des Medianwerts in zwei Hälften. Suchen Sie aus der unteren Hälfte der Wertemenge den Median für die untere Menge, die der Q1-Wert ist.
Schritt 4: Ermitteln Sie den oberen Quartilwert Q3 aus dem Datensatz. Es ist genau wie der obige Schritt. Anstelle der unteren Hälfte müssen wir auf die gleiche Weise den Wertesatz der oberen Hälfte befolgen.
Schritt 5: Ermitteln Sie den IQR-Wert für den Interquartilbereich. Den Q1-Wert von Q3 abziehen.
IQR = Q3-Q1
Schritt 6: Finden Sie den inneren Extremwert. Ein Ende, das außerhalb der unteren Seite liegt und auch als kleiner Ausreißer bezeichnet werden kann. Multiplizieren Sie den IQR-Wert mit 1, 5 und ziehen Sie diesen Wert von Q1 ab, um das innere untere Extrem zu erhalten.
Unterer Ausreißer = Q1 - (1, 5 * IQR)
Schritt 7: Finden Sie den äußeren Extremwert. Ein Ende, das außerhalb der höheren Seite liegt und auch als größerer Ausreißer bezeichnet werden kann. Multiplizieren Sie den IQR-Wert mit 1, 5 und addieren Sie diesen Wert mit Q3.
Höherer Ausreißer = Q3 + (1, 5 * IQR)
Schritt 8: Werte, die außerhalb dieser inneren und äußeren Extreme liegen, sind die Ausreißerwerte für den gegebenen Datensatz.
Relevanz und Verwendung der Ausreißerformel
Ausreißer sind bei allen Datenanalyseproblemen sehr wichtig. Ausreißer zeigt Inkonsistenz in jedem Datensatz an, da dieser als ungewöhnlich entfernte Werte im Datensatz von einem zum anderen definiert ist. Dies ist sehr nützlich, um Fehler im Datensatz zu finden. Wenn Sie einen Fehler in den Datensatz einfügen, wirkt sich dies auf den Mittelwert und den Median aus und kann daher zu großen Abweichungen im Ergebnis führen, wenn sich Ausreißer im Datensatz befinden. Daher ist es wichtig, Ausreißer aus dem Datensatz zu ermitteln, um schwerwiegende Probleme bei der statistischen Analyse zu vermeiden.
Empfohlene Artikel
Dies war ein Leitfaden für die Formel "Ausreißer". Hier diskutieren wir, wie man Ausreißer berechnet, zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Leitfaden für die Midrange-Formel
- Beispiele für Gehaltsformeln
- Rechner für DPMO-Formel
- Wie berechnet man die T-Verteilung?
- Quartilabweichungsformel | Beispiele