
Variationskoeffizient Formel (Inhaltsverzeichnis)
- Formel
- Beispiele
Was ist die Variationskoeffizientenformel?
In der Statistik ist der Variationskoeffizient, der auch als CV bezeichnet wird, ein Hilfsmittel, mit dessen Hilfe wir bestimmen können, wie Datenpunkte in einem Datensatz um den Mittelwert verteilt sind. Grundsätzlich werden zuerst alle Datenpunkte aufgetragen und dann der Variationskoeffizient verwendet, um die Streuung dieser Punkte voneinander und den Mittelwert zu messen. Es hilft uns also, die Daten zu verstehen und das Muster zu erkennen, das sie bilden. Sie wird als Verhältnis der Standardabweichung des Datensatzes zum Mittelwert berechnet. Je höher der Variationskoeffizient, desto größer ist die Streuung der Daten um den Mittelwert. Je niedriger der Wert des Variationskoeffizienten ist, desto geringer ist die Streuung und desto genauer sind die Ergebnisse. Auch wenn der Mittelwert zweier Datenreihen erheblich unterschiedlich ist, ist der Variationskoeffizient sehr nützlich, um den Variationsgrad von einer Datenreihe zur anderen zu vergleichen.
Formel für den Variationskoeffizienten ist gegeben durch:
Coefficient of Variation = Standard Deviation / Mean
Schritte zur Berechnung des Variationskoeffizienten:
Schritt 1: Berechnen Sie den Mittelwert des Datensatzes. Der Mittelwert ist der Durchschnitt aller Werte und kann berechnet werden, indem die Summe aller Werte durch eine Anzahl von Datenpunkten dividiert wird.
Schritt 2: Berechnen Sie anschließend die Standardabweichung des Datensatzes. Das ist ein wenig zeitaufwändiger Vorgang. Die Standardabweichung kann wie folgt berechnet werden: √ (Σ (X i - X m ) 2 / (n - 1)) . X i ist der i-te Datenpunkt und X m ist der Mittelwert des Datensatzes. Alternativ können wir die Standardabweichung auch mit der Funktion STDEV.S () in Excel ermitteln.
Schritt 3: Teilen Sie die Standardabweichung durch den Mittelwert, um den Variationskoeffizienten zu erhalten.
Beispiele für Variationskoeffizientenformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des Variationskoeffizienten besser zu verstehen.
Sie können diese Excel-Vorlage für Variationskoeffizientenformeln hier herunterladen - Excel-Vorlage für VariationskoeffizientenformelnVariationskoeffizient Formel - Beispiel # 1
Angenommen, wir haben zwei Datensätze A und B und jeder enthält 20 zufällige Datenpunkte. Berechnen Sie den Variationskoeffizienten für den Datensatz X & Y.
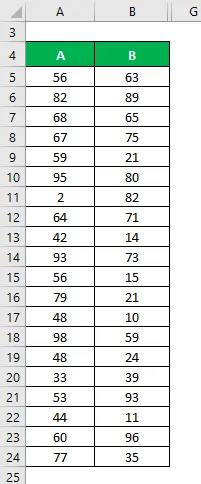
Lösung:
Mittelwert wird berechnet als:
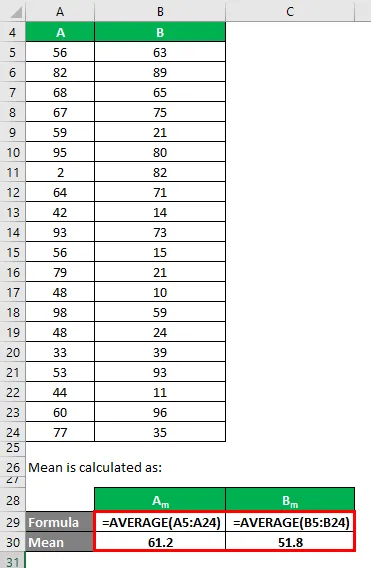
- Mittelwert von Datensatz A = 61, 2
- Mittelwert des Datensatzes B = 51, 8
Jetzt müssen wir die Differenz zwischen den Datenpunkten und dem Mittelwert berechnen.
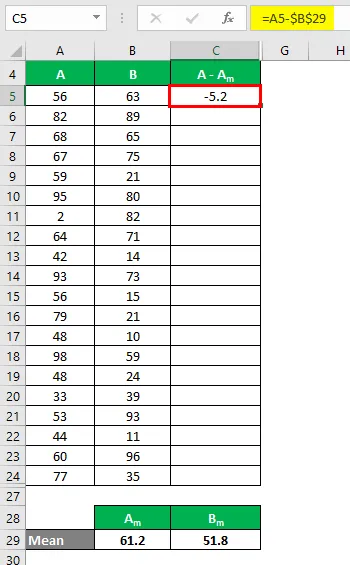
Berechnen Sie in ähnlicher Weise für alle Werte des Datensatzes A.
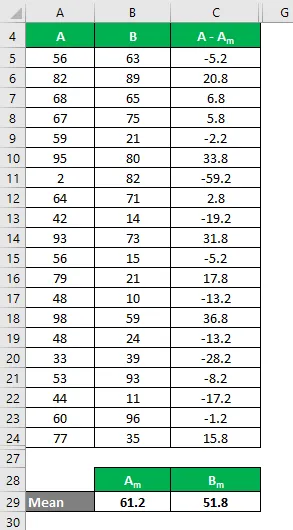
Berechnen Sie in ähnlicher Weise für alle Werte des Datensatzes B.
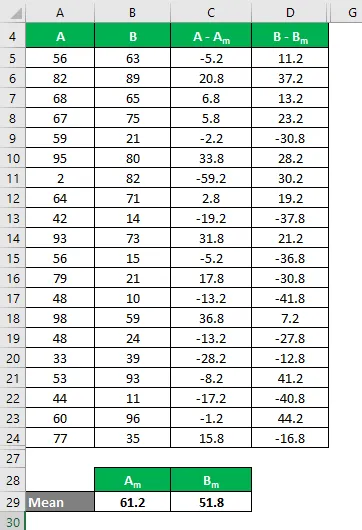
Berechnen Sie das Quadrat der Differenz für beide Datensätze A und B.
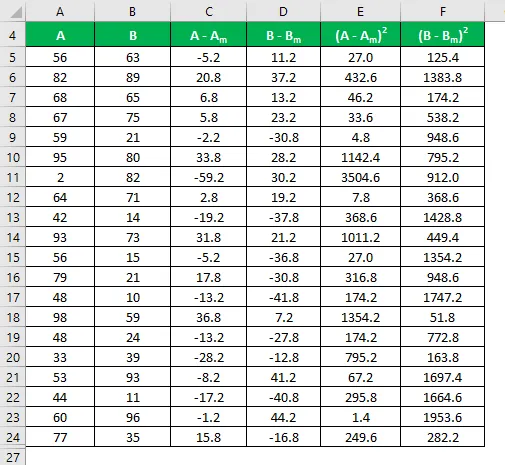
Die Standardabweichung wird mit der unten angegebenen Formel berechnet
Standardabweichung = √ (Σ (X i - X m ) 2 / (n - 1))
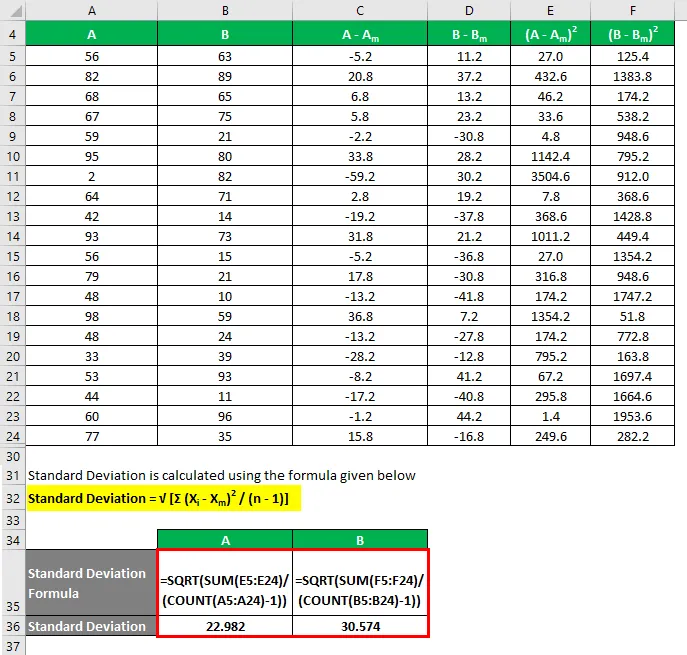
Der Variationskoeffizient wird mit der unten angegebenen Formel berechnet
Variationskoeffizient = Standardabweichung / Mittelwert
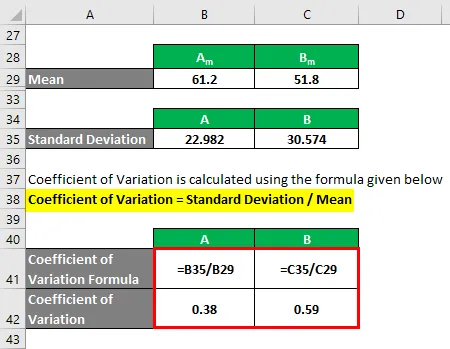
- Variationskoeffizient A = 22, 982 / 61, 2 = 0, 38
- Variationskoeffizient B = 30, 574 / 51, 8 = 0, 59
Wenn Sie also hier sehen, hat B einen höheren Variationskoeffizienten als A, was bedeutet, dass die Datenpunkte von B weiter verteilt sind als A.
Variationskoeffizient Formel - Beispiel # 2
Angenommen, Sie sind ein risikoaverser Investor und möchten Geld an der Börse anlegen. Da Ihr Risikoappetit gering ist, möchten Sie in sichere Aktien investieren, die eine geringere Standardabweichung und einen geringeren Variationskoeffizienten aufweisen. Sie haben 3 Aktien aufgrund ihrer fundamentalen und technischen Informationen in die engere Wahl gezogen und möchten 2 Aktien auswählen. Sie haben auch Informationen zu den historischen Erträgen der letzten 15 Jahre gesammelt.
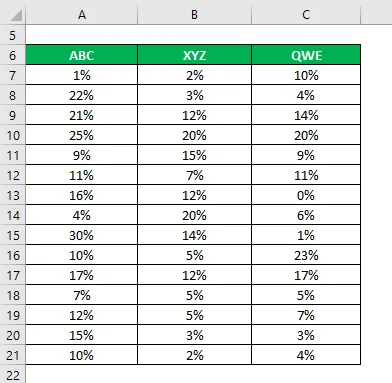
Lösung:
Mittelwert wird berechnet als:
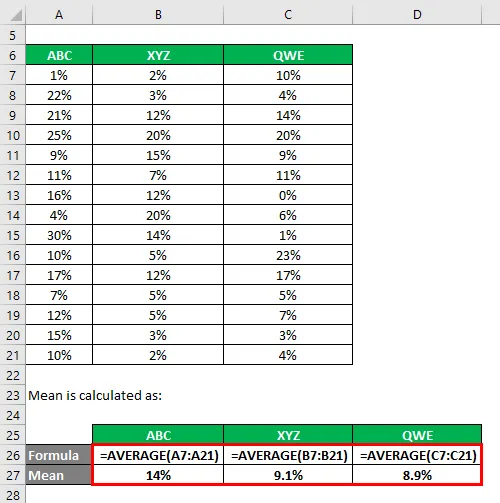
Die Standardabweichung wird mit der Excel-Formel berechnet
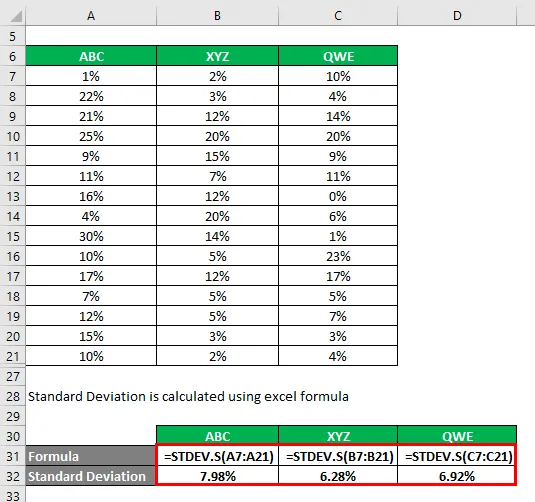
Der Variationskoeffizient wird mit der unten angegebenen Formel berechnet
Variationskoeffizient = Standardabweichung / Mittelwert
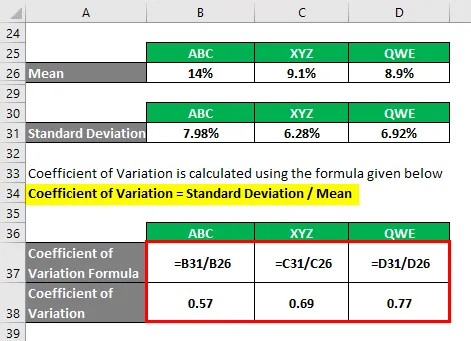
- Variationskoeffizient ABC = 7, 98% / 14% = 0, 57
- Variationskoeffizient XYZ = 6, 28% / 9, 1% = 0, 69
- Variationskoeffizient QWE = 6, 92% / 8, 9% = 0, 77
Basierend auf den Informationen wählen Sie Aktien ABC und XYZ, um zu investieren, da diese den niedrigsten Variationskoeffizienten aufweisen.
Erläuterung
Da der Variationskoeffizient ein Maß für das Risiko ist, hilft er bei der Messung der Volatilität der Kurse von Aktien und anderen Finanzinstrumenten. Darüber hinaus können Anleger und Analysten die mit verschiedenen potenziellen Anlagen verbundenen Risiken vergleichen.
Der Variationskoeffizient ähnelt der Standardabweichung, eine Standardabweichung von zwei Variablen kann jedoch nicht sinnvoll verglichen werden. Die Verwendung von Standardabweichung und Mittelwert macht den relativen Vergleich jedoch aussagekräftiger. Es gibt auch eine Beschränkung des Variationskoeffizienten. Angenommen, der Mittelwert eines Datensatzes ist Null. In diesem Fall wird dieses Tool unwirksam. Nicht nur das, wenn wir einen Datensatz haben, der viele positive und negative Werte hat, wird der Variationskoeffizient sehr problematisch. Daher ist es nur bei Datensätzen mit dem gleichen Plus-Minus-Vorzeichen sinnvoller.
Relevanz und Verwendung der Variationskoeffizientenformel
Der Variationskoeffizient ist in vielen anderen Bereichen als der Statistik relevant. Beispielsweise ist im Finanzbereich der Variationskoeffizient ein Maß für das Risiko. Es ähnelt der Standardabweichung, da dies auch als Maß für das Risiko herangezogen wird. Der Unterschied besteht jedoch darin, dass der Variationskoeffizient ein besserer Indikator für das relative Risiko ist. Angenommen, A hat eine erwartete Rendite von 15% und B eine erwartete Rendite von 10%, und A hat eine Standardabweichung von 10%, während B eine Standardabweichung von 5% hat. Um eine bessere Investition zu wählen, kann der Variationskoeffizient verwendet werden. Der Variationskoeffizient von A beträgt also 10/15 = 0, 666 und der Variationskoeffizient von B beträgt 5/10 = 0, 5. B ist also eine bessere Investition als A.
Empfohlene Artikel
Dies war ein Leitfaden für die Variationskoeffizientenformel. Hier diskutieren wir, wie der Variationskoeffizient mithilfe einer Formel berechnet wird, zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Was ist eine angepasste R-Quadrat-Formel?
- Beispiele der Bestimmungskoeffizientenformel
- Wie berechnet man den Korrelationskoeffizienten mithilfe einer Formel?
- Kovarianzformel mit Excel-Vorlage