Einführung in Merge Sort in Java
Das Programm für Merge Sort in Java ist einer der am weitesten verbreiteten und effizientesten Algorithmen. Die Zusammenführungssortierung basiert auf der Divide- und Conquer-Technik, bei der ein gegebenes Problem in mehrere Teilprobleme unterteilt und jedes Teilproblem unabhängig gelöst wird. Wenn die Teilprobleme gelöst sind, kombinieren wir ihre Ergebnisse, um die endgültige Lösung des Problems zu erhalten. Der Sortieralgorithmus für das Zusammenführen kann mithilfe der Rekursion implementiert werden, da mit Unterproblemen und nicht mit dem Hauptproblem gearbeitet wird.
Wie funktioniert die Zusammenführungssortierung?
Betrachten wir ein unsortiertes Array, das mit dem Mergesortierungsalgorithmus sortiert werden muss. So sortieren Sie ein Array mit folgenden Werten: 18, 8, 4, 13, 10, 12, 7 und 11:
- Der erste Schritt besteht darin, ein Pivot-Element zu finden, auf dessen Grundlage unser Eingabearray in Unterarrays unterteilt wird.
- Nehmen wir an, dass das Element 13 als Drehpunkt ausgewählt ist, daher wird das ursprüngliche Array in zwei Unterarrays unterteilt. Das erste Subarray enthält 18, 8, 4, 13 und das zweite Subarray enthält die verbleibenden Elemente 10, 12, 7, 11.
- In Schritt 2 erhaltene Subarrays werden wie in Schritt 1 weiter unterteilt, und dies wird fortgesetzt.
- Sobald das Hauptarray in Unterarrays mit einzelnen Elementen unterteilt ist, werden diese Unterarrays wieder zusammengeführt, sodass die zusammengeführten Elemente in sortierter Reihenfolge vorliegen.
- So funktioniert das eigentliche Teilen und Erobern:
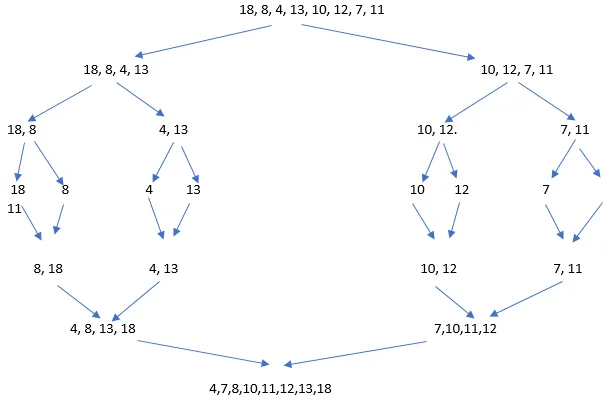
Programm für Merge Sort in Java
Hier ist ein Codebeispiel, das die Implementierung der Zusammenführungssortierung in Java zeigt:
Code:
package com.edubca.sorting;
public class MergeSort (
private int() array;
private int() tempMergedArr;
private int length;
public static void main(String a())(
int() inputArr = (18, 8, 4, 13, 10, 12, 7, 11);
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr)(
System.out.print(i + " ");
)
)
public void sort(int inputArr()) (
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int(length);
performMergeSort(0, length - 1);
)
private void performMergeSort(int lowerIndex, int higherIndex) (
if (lowerIndex < higherIndex) (
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
)
)
private void mergeData (int lowerIndex, int middle, int higherIndex) (
for (int i = lowerIndex; i <= higherIndex; i++) (
tempMergedArr(i) = array(i);
)
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) (
if (tempMergedArr(i) <= tempMergedArr(j)) (
array(k) = tempMergedArr(i);
i++;
) else (
array(k) = tempMergedArr(j);
j++;
)
k++;
)
while (i <= middle) (
array(k) = tempMergedArr(i);
k++;
i++;
)
)
)
Der obige Code erzeugt ein sortiertes Array als Ausgabe.
Ausgabe:

Wann sollten wir die Zusammenführungssortierung verwenden?
Die Zusammenführungssortierung kann in den folgenden Szenarien verwendet werden:
- Wenn die zu sortierende Datenstruktur keinen wahlfreien Zugriff unterstützt, kann die Sortierung beim Zusammenführen hilfreich und effizient sein.
- Wenn ein hohes Maß an Parallelität erforderlich ist, kann die Zusammenführungssortierung verwendet werden, da verschiedene Unterprobleme unabhängig voneinander unter Verwendung mehrerer parallel ablaufender Prozesse gelöst werden können.
- Die Sortierung beim Zusammenführen ist beim Arbeiten mit verknüpften Listen schneller, da Zeiger beim Zusammenführen der Listen leicht geändert werden können.
- Merge Sort kann als stabile Sortierung betrachtet werden, dh dass dasselbe Element in einem Array seine ursprünglichen Positionen zueinander beibehält. In Fällen, in denen eine hohe Stabilität erforderlich ist, kann eine Zusammenführungssortierung gewählt werden.
Komplexitätsanalyse der Zusammenführungssortierung
Unter Punkte Analyse Komplexität der Zusammenführung sortieren:
- Die Zusammenführungssortierung ist ein rekursiver Algorithmus und hat in allen drei Fällen (schlechteste, beste und durchschnittliche) eine Zeitkomplexität von 0 (n * log n), da die Zusammenführungssortierung das Array in zwei gleiche Hälften unterteilt und für die Zusammenführung eine lineare Zeit benötigt.
- Die Raumkomplexität der Zusammenführungssortierung ist O (n), da sie nach dem rekursiven Ansatz arbeitet. Daher kann die Zusammenführungssortierung als schneller, raum- und zeiteffizienter Algorithmus angesehen werden.
Vergleichen der Zusammenführungssortierung mit anderen Algorithmen
Die folgenden Punkte vergleichen die Zusammenführungssortierung mit anderen Algorithmen:
- Heap-Sortierung hat die gleiche zeitliche Komplexität wie Merge-Sortierung, benötigt jedoch nur O (1) zusätzlichen Speicherplatz anstelle von O (n) für Merge-Sortierung. Daher ist die Heap-Sortierung platzsparender als die Merge-Sortierung.
- Quick Sort-Implementierungen übertreffen im Allgemeinen Merge Sort, um RAM-basierte Arrays zu sortieren.
- Merge Sort übertrifft die schnellen Sortier- und Heap-Sortieralgorithmen, wenn mit der verknüpften Liste gearbeitet wird, da Zeiger leicht geändert werden können.
Fazit-Programm für Merge Sort in Java
Aus dem Artikel wird geschlossen, dass die Zusammenführungssortierung ein wichtiges Konzept ist, um zu verstehen, wenn es um Algorithmen geht.
Empfohlene Artikel
Dies ist eine Anleitung zu Program for Merge Sort in Java. Hier besprechen wir, wie es funktionieren soll, wie es verwendet wird, wie es zusammengeführt werden soll usw. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren
- Sortieren in Java zusammenführen
- Sortieralgorithmen in Java zusammenführen
- Heap-Sortierung in C
- Heap-Sortierung in Java
- Java-Bereitstellungstools
- Heap-Sortierung in Python
- Schnelle Sortieralgorithmen in Java
- Top 6 Sortieralgorithmus in JavaScript
- Top 6 Sortieralgorithmen in Python