
Arithmetische Mittelwertformel (Inhaltsverzeichnis)
- Formel
- Beispiele
- Taschenrechner
Was ist die arithmetische Mittelwertformel?
Der Begriff „arithmetisches Mittel“ bezieht sich grundsätzlich auf den mathematischen Durchschnitt von zwei oder mehr Zahlen. Die Methode zur Berechnung des arithmetischen Mittels kann jedoch je nach Häufigkeit der einzelnen Variablen im Datensatz variieren - einfacher Durchschnitt (gleich gewichtet) oder gewichteter Durchschnitt. Die Formel für das arithmetische Mittel für gleichgewichtete Variablen kann abgeleitet werden, indem alle Variablen im Datensatz summiert werden und das Ergebnis durch die Anzahl der Variablen dividiert wird. Mathematisch wird es dargestellt als
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
oder
Arithmetic Mean =∑ x i / n
Wo,
- x i = i- te Variable
- n = Anzahl der Variablen im Datensatz
Bei ungleich gewichteten Variablen kann die Formel für das arithmetische Mittel abgeleitet werden, indem die Produkte jeder Variablen und ihre Häufigkeit aufsummiert werden und das Ergebnis durch die Summe der Häufigkeiten dividiert wird. Mathematisch wird es dargestellt als
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
oder
Arithmetic Mean = ∑ (f i * x i ) / f i
Wo
- x i = i- te Variable
- f i = Häufigkeit der i- ten Variablen
Beispiele für arithmetische Mittelwertformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des arithmetischen Mittels besser zu verstehen.
Sie können diese Excel-Vorlage für arithmetische Mittelwertformeln hier herunterladen - Excel-Vorlage für arithmetische MittelwertformelnArithmetische Mittelwertformel - Beispiel # 1
Nehmen wir ein Beispiel für einen Schlagmann, der in seinen letzten 10 Innings im letzten Jahr die folgenden Läufe erzielt hat: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Berechnen Sie den Durchschnitt des Schlagmanns in seinem letzten 10 Innings.
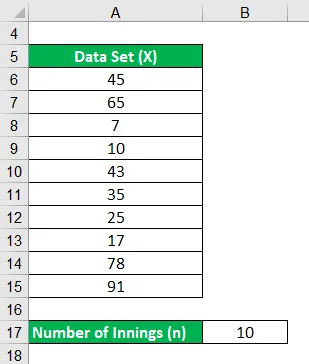
Lösung:
Das arithmetische Mittel wird nach der unten angegebenen Formel berechnet
Arithmetisches Mittel = ∑ x i / n
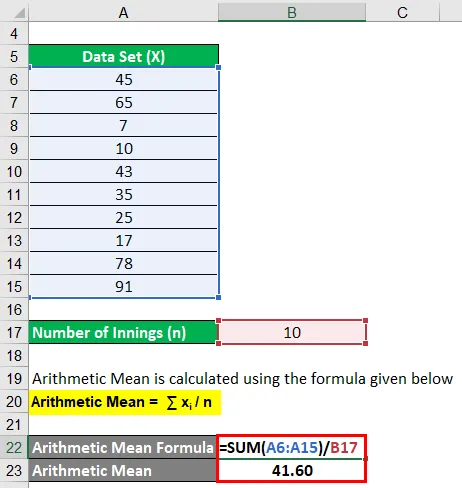
- Arithmetisches Mittel = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Arithmetisches Mittel = 41, 60
Daher blieb der Durchschnitt des Schlagmanns 41, 60 Runs pro Innings in seinen letzten 10 Innings.
Arithmetische Mittelwertformel - Beispiel # 2
Nehmen wir ein Beispiel einer Klasse mit 45 Schülern. Kürzlich wurde ein wöchentlicher wissenschaftlicher Test durchgeführt, bei dem die Schüler auf der Skala von 1 bis 10 bewertet wurden. Berechnen Sie die Durchschnittsnoten im Test auf der Grundlage der folgenden Informationen.
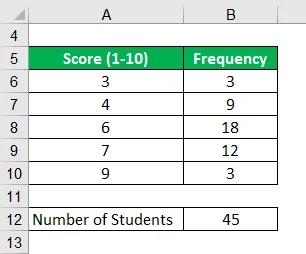
Lösung:
Das arithmetische Mittel wird nach der unten angegebenen Formel berechnet
Arithmetisches Mittel = ∑ (fi * xi ) / fi
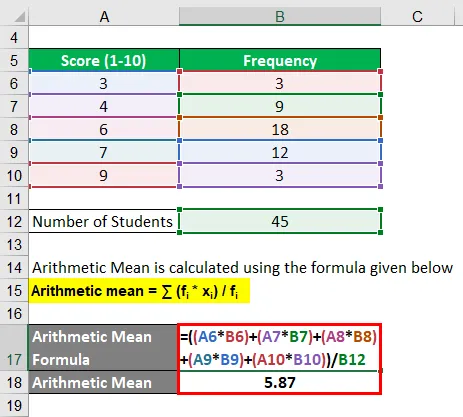
- Arithmetisches Mittel = ((3 · 3) + (4 · 9) + (6 · 18) + (7 · 12) + (9 · 3)) / 45
- Arithmetisches Mittel = 264/45
- Arithmetisches Mittel = 5, 87
Daher betrug die durchschnittliche Punktzahl der Klasse im Wissenschaftstest 5, 87.
Arithmetische Mittelwertformel - Beispiel # 3
Nehmen wir ein Beispiel von zwei Datensätzen mit zwei verschiedenen arithmetischen Mitteln. Der erste Datensatz enthält 10 Variablen mit einem Mittelwert von 45, während der zweite Datensatz 7 Variablen und einen Mittelwert von 42 enthält. Ermitteln Sie den arithmetischen Mittelwert der beiden kombinierten Datensätze.
Lösung:
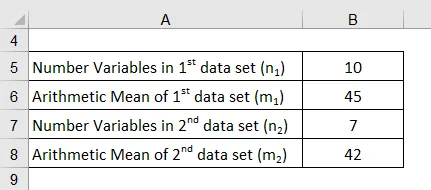
Die arithmetischen Mittelwerte des kombinierten Datensatzes werden unter Verwendung der unten angegebenen Formel berechnet
Arithmetisches Mittel = ((m 1 · n 1 ) + (m 2 · n 2 )) / (n 1 + n 2 )
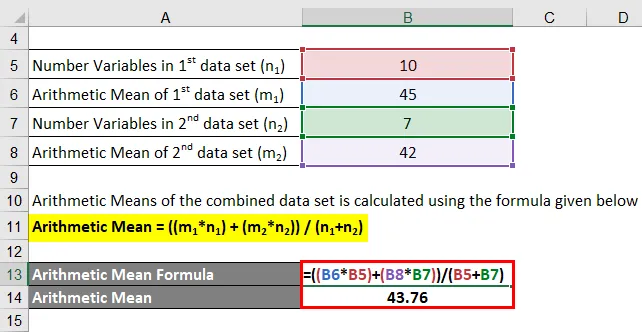
- Arithmetisches Mittel = (45 * 10 + 42 * 7) / (10 + 7)
- Arithmetisches Mittel = 43, 76
Das arithmetische Mittel des kombinierten Datensatzes ist daher 43, 76.
Erläuterung
Die Formel für das arithmetische Mittel kann mithilfe der folgenden Schritte berechnet werden:
Schritt 1: Sammeln und sortieren Sie zunächst die Variablen, für die das arithmetische Mittel berechnet werden soll. Die Variablen sind mit x i bezeichnet .
Schritt 2: Bestimmen Sie als Nächstes die Anzahl der Variablen im Datensatz, die bei gleichgewichteten Variablen mit n bezeichnet wird. Ansonsten ermitteln Sie die Häufigkeit jeder Variablen und sie werden mit fi bezeichnet, und die Anzahl der Variablen ist die Summe der Häufigkeiten.
Schritt 3: Schließlich kann die Formel für das arithmetische Mittel für gleichgewichtete Variablen abgeleitet werden, indem alle Variablen addiert werden. Anschließend wird das Ergebnis durch die Anzahl der Variablen im Datensatz dividiert, wie unten gezeigt.
Arithmetisches Mittel = ∑ x i / n
Im Falle eines gewichteten Durchschnitts kann die Formel für das arithmetische Mittel abgeleitet werden, indem die Produkte jeder Variablen und ihre Häufigkeit aufsummiert werden und das Ergebnis dann durch die Summe der Häufigkeiten dividiert wird, wie nachstehend gezeigt.
Arithmetisches Mittel = ∑ f i * x i / f i
Relevanz und Verwendung der arithmetischen Mittelwertformel
Das Konzept des arithmetischen Mittels ist sehr einfach und elementar. Es ist jedoch nach wie vor sehr wichtig, da es häufig als statistischer Indikator zur Bewertung des durchschnittlichen Ergebnisses in einem Datensatz verwendet wird. Tatsächlich ermöglicht es die Bewertung, welche der Variablen besser oder niedriger als der Durchschnitt der Gruppe sind. Es wird auch als Maß für den Durchschnittswert über die gesamte Datenreihe verwendet. Ferner wird der arithmetische Mittelwert in Fällen verwendet, in denen der geometrische Mittelwert oder der harmonische Mittelwert weniger nützlich sind, wie z. B. Durchschnittsnote, Gewicht usw.
Rechner der arithmetischen Mittelwertformel
Sie können den folgenden arithmetischen Mittelwertrechner verwenden
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Arithmetisches Mittel | |
| Arithmetisches Mittel | = |
|
|
Empfohlene Artikel
Dies ist eine Anleitung zur arithmetischen Mittelwertformel. Hier diskutieren wir, wie man das arithmetische Mittel berechnet, zusammen mit praktischen Beispielen. Wir bieten auch einen Arithmetic Mean Calculator mit herunterladbarer Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Wie berechnet man den harmonischen Mittelwert?
- Leitfaden zur Durchschnittsformel der Bevölkerung
- Mittelwertbildung mit Formel
- Beispiele für die Nettoumsatzformel