Einführung in mathematische Funktionen in C ++
Es ist schwierig und zeitaufwendig, wenn Sie jedes Mal Code schreiben müssen, um grundlegende mathematische Berechnungen in Ihrem Programm durchzuführen. Daher bietet C ++ eine Vielzahl von mathematischen Funktionen, um Ihren Code einfach und effizient zu gestalten. Mit mathematischen Funktionen können Sie eine große Anzahl von Operationen mit Zahlen ausführen. Da diese Funktionen in C ++ integriert sind und von der Bibliothek unterstützt werden, ist es erforderlich, die Header-Datei oder am Anfang des Codes alle Funktionen der mathematischen Funktionen zu verwenden. Es ist nicht erforderlich, die Logik in Code zu schreiben, um Operationen auszuführen, sondern es befindet sich alles in der Bibliothek.
Verschiedene Arten von mathematischen Funktionen
C ++ bietet eine Vielzahl von verschiedenen Arten von mathematischen Funktionen, die im Folgenden anhand von Beispielen aufgeführt werden:
1. Maximum & Minimum Funktion
- max (p, q): Gibt eine maximale Anzahl zwischen p und q zurück.
- min (p, q): Gibt eine minimale Zahl zwischen p und q zurück.
C ++ - Code zur Implementierung der obigen Funktionalität
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Ausgabe:

2. Power-Funktionen
- pow (m, n): Berechnet m auf die Potenz n angehoben.
- sqrt (m): Berechnet die Quadratwurzel von m.
- cbrt (n): Berechnet die Kubikwurzel von n.
- hypot (m, n): Berechnet die Hypotenuse des rechtwinkligen Dreiecks.
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
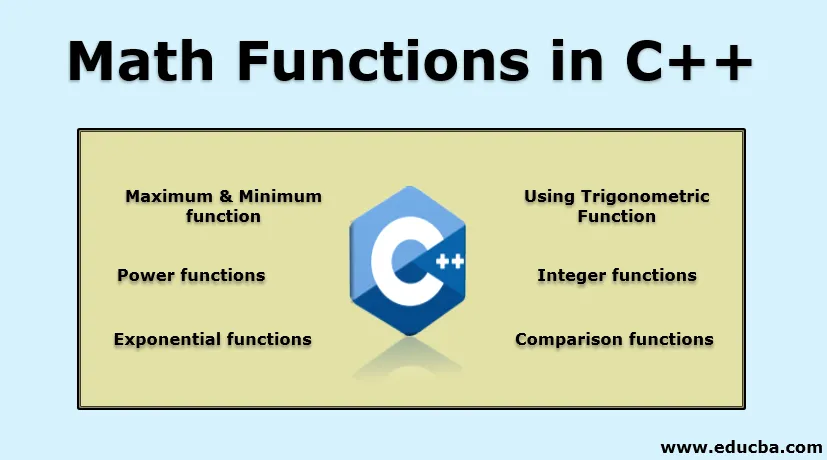
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
Ausgabe:

3. Exponentialfunktionen
- exp (p): Berechnet das exponentielle e, das zur Potenz p angehoben wird.
- log (p): Berechnet den Logarithmus von p.
- log10 (p): Berechnet den gemeinsamen Logarithmus von p.
- exp2 (p): Berechnet die Basis 2 Exponential von p.
- log2 (p): Es wird der Logarithmus zur Basis 2 von p berechnet.
- logb (p): Es wird der Logarithmus von p berechnet.
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Ausgabe:
4. Integer-Funktionen
Es hilft bei der Suche nach dem nächsten ganzzahligen Wert.
- ceil (z): rundet den Wert von z auf.
- floor (z): rundet den Wert von z ab.
- round (z): Rundet den Wert von z.
- fmod (z, y): Berechnet den Rest der Division z / y.
- trunc (z): Es rundet den z-Wert gegen Null ab.
- rint (z): Mit dem Rundungsmodus wird der z-Wert gerundet.
- nearint (z): Es wird der z-Wert auf einen nahe gelegenen Integralwert gerundet.
- Rest (z, y): Es wird der Rest von z / y berechnet.
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
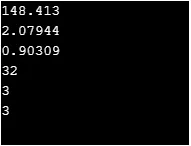
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Ausgabe:
5. Vergleichsfunktionen
Hilfe beim Vergleichen von Zahlen in einem kurzen Zeitraum spielt keine Rolle, wie lange die Zahl ist. Nachfolgend einige Beispiele für Vergleichsfunktionen:
- isgreater (p, q): Prüft, ob p größer als q ist oder nicht.
- islessequal (p, q): Prüft, ob p kleiner oder gleich q ist oder nicht.
- isgreaterequal (p, q): Überprüft, ob p größer oder gleich q ist oder nicht.
- islessgreater (p, q): Prüft, ob p kleiner oder größer als y ist oder nicht.
- isunordered (p, q): Prüft, ob p verglichen wird oder nicht.
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
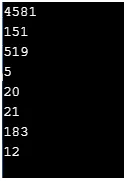
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Ausgabe:

6. Verwenden der trigonometrischen Funktion
Funktionen, die speziell für geometrische Berechnungen verwendet werden. Das rechtwinklige Dreieck gibt eine Beziehung zwischen dem Winkel und dem Verhältnis der Länge der beiden Seiten an.
- sin (y): Berechnet den Wert von sin y.
- cos (y): Berechnet den Wert von Cosinus y.
- tan (y): Berechnet den Wert der Tangente y.
- asin (y): Berechnet den Wert des inversen Sinus y.
- acos (y): Berechnet den Wert des inversen Cosinus y.
- atan (y): Berechnet den Wert der inversen Tangente y.
- atan2 (y, x): Berechnet den Wert des inversen Tangens der y- und x-Koordinaten.
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
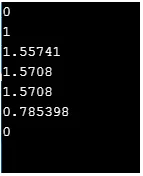
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Ausgabe:
Im Folgenden sind einige weitere interessante Funktionen aufgeführt, die bei der Berechnung der Werte von hyperbolischen trigonometrischen Funktionen hilfreich sind. Sie werden als hyperbolische Funktionen bezeichnet.
- sinh (x): Berechnet den Wert des hyperbolischen Sinus von x.
- cosh (x): Berechnet den Wert des hyperbolischen Cosinus von x.
- tanh (x): Berechnet den Wert des hyperbolischen Tangens von x.
- asinh (x): Berechnet den Wert des Hyperbelsinus von x.
- acosh (x): Berechnet den Wert des Cosinus hyperbolicus von x.
- atanh (x): Berechnet den Wert des Hyperbelsinus von x.
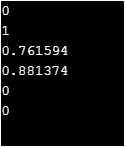
C ++ - Code zum Implementieren der obigen Funktionalität
#include
#include
using namespace std;
int main() (
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
Ausgabe:
Fazit
Mathematische Funktionen spielen eine wichtige Rolle, um viel Zeit und Platz im Speicher zu sparen. Alle Funktionen sind integriert. Sie müssen keine mathematischen Funktionen direkt implementieren, indem Sie eine Header-Datei hinzufügen, die die Option bietet, die gesamte Bibliothek der mathematischen Klasse zu verwenden.
Empfohlene Artikel
Dies ist eine Anleitung zu mathematischen Funktionen in C ++. Hier diskutieren wir, dass C ++ eine große Anzahl verschiedener Arten von mathematischen Funktionen mit Beispielen bietet. Sie können auch unsere anderen Artikelvorschläge durchgehen -
- Überschreiben in C ++
- Überladen in C ++
- Quadratwurzel in C ++
- Arrays in C ++
- Überladen in Java
- Quadratwurzel in PHP
- Top 11 Features und Vorteile von C ++
- Anleitung zur Quadratwurzel in JavaScript