
Einführung in Squares in Java
Wenn eine Zahl mit sich selbst multipliziert wird, ist die resultierende Zahl das Quadrat der Zahl. Quadrate einer Zahl sind sehr leicht zu finden. Im Allgemeinen erhalten wir das Ergebnis immer dann, wenn wir die Quadratwurzel einer Ganzzahl finden, nur in Ganzzahl. Wenn wir das Quadrat einer Dezimalzahl finden, erhalten wir die Antwort ebenfalls als Dezimalzahl. Eine interessante Tatsache über das Quadrat einer Zahl ist, dass sich der Wert der resultierenden Zahl erhöht, wenn wir ein Quadrat einer ganzen Zahl machen. Wenn wir jedoch das Dezimalquadrat zwischen 0 und 1 eingeben, nimmt die sich ergebende Zahl ab. Ein Beispiel wäre die Quadratur von 0, 5. Wenn wir 0, 5 quadrieren, wird die Zahl auf 0, 25 verringert. In diesem Artikel werden die verschiedenen Methoden zum Quadrieren einer Zahl mit der Programmiersprache Java vorgestellt.
Working - Quadrat einer Zahl kann in Java durch eine Vielzahl von Techniken ermittelt werden. Wir möchten einige Beispiele sehen, die sich auf das Quadrat einer Zahl beziehen, unter denen wir das Quadrat einer Zahl besser verstehen können.
Wie berechnet man Square in Java?
Lassen Sie uns lernen, wie man ein Quadrat in Java berechnet:
Beispiel 1
Der einfachste Weg, das Quadrat einer Zahl zu finden, ist Math.pow (), mit dem sich jede Potenz einer Zahl berechnen lässt.
Code:
import java.util.*;
public class Square
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int num;
System.out.print("Enter a number which is integer format: ");
num=sc.nextInt();
System.out.println("The square of "+ num + " is: "+ Math.pow(num, 2));
)
)
Ausgabe:

Beispiel # 2
Im nächsten Programm berechnen wir das Quadrat einer Zahl in der üblichen Form so, dass es zwei Zahlen nacheinander multipliziert und das Quadrat der jeweiligen Zahl findet.
Code:
import java.util.*;
public class Square2
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int no;
System.out.print("Enter a number which is integer format: ");
no=sc.nextInt();
System.out.println("Square of "+ no + " is: "+(no*no));//the number is multiplied with its own
)
)
Ausgabe:

Beispiel # 3
In diesem Beispiel prüfen wir, ob eine Zahl ein perfektes Quadrat ist oder nicht. Dies ist ein etwas komplexes Programm, da es prüft, ob eine Zahl ein Quadrat einer anderen Zahl ist.
Code:
import java.util.Scanner;
class JavaExample (
static boolean checkPerfectSquare(double x)
(
// finding the square root of given number
double s= Math.sqrt(x);
return ((s - Math.floor(s)) == 0); //Math.floor() is used here to calculate the lower value.
)
public static void main(String() args)
(
System.out.print("Enter any number:");
Scanner scanner = new Scanner(System.in);
double no= scanner.nextDouble();
scanner.close();
if (checkPerfectSquare(no))
System.out.print(no+ " is a perfect square number");
else
System.out.print(no+ " is not a perfect square number");
)
)
Ausgabe:

Beispiel # 4
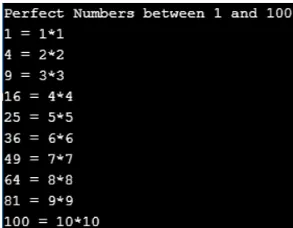
In diesem Programm finden wir die Anzahl der Quadratzahlen innerhalb eines bestimmten Bereichs. Wir geben den Zahlenbereich ein und der Code würde die Quadratzahl in diesem spezifischen Bereich erzeugen. Im folgenden Programm finden wir die Anzahl der Quadratzahlen zwischen 0 und 100.
Code:
// Finding the range of perfect square numbers in Java programming language
import java.io.IOException;
public class SquareNumbersInRange (
public static void main(String() args) throws IOException (
int starting_number = 1;
int ending_number = 100;
System.out.println("Perfect Numbers between "+starting_number+ " and "+ending_number);
for (int i = starting_number; i <= ending_number; i++) (
int number = i;
int sqrt = (int) Math.sqrt(number);
if (sqrt * sqrt == number) (
System.out.println(number+ " = "+sqrt+"*"+sqrt);
)
)
)
)
Ausgabe:
Beispiel # 5
In diesem Programm sehen wir die Summe der Quadrate der ersten N natürlichen Zahlen. Wir geben den Wert von N ein und das Programm berechnet die Summe der Quadrate der ersten N natürlichen Zahlen.
Code:
// Java Program to find sum of
// square of first n natural numbers
import java.io.*;
class SumofSquares
(
// Return the sum of the square of first n natural numbers
static int square sum(int n)
(
// Move the loop of I from 1 to n
// Finding square and then adding it to 1
int sum = 0;
for (int i = 1; i <= n; i++)
sum += (i * i);
return sum;
)
// Main() used to print the value of sum of squares
public static void main(String args()) throws IOException
(
int n = 6;
System.out.println("The sum of squares where N value is 6 is "+ squaresum(n));
)
)
Ausgabe:

Fazit
- In diesem Artikel sehen wir eine Liste von Methoden, mit denen wir eine Zahl quadrieren können, wie wir herausfinden können, ob eine Zahl innerhalb eines bestimmten Bereichs quadratisch ist oder nicht, und auch die Summe der ganzen Zahlen der ersten N natürlichen Zahlen. Es gibt jedoch auch einige andere Techniken, mit denen das Quadrat einer Zahl ermittelt werden kann. Der Name einer Technik, die verwendet werden kann, um zu sehen und zu prüfen, ob eine Zahl ein Quadrat ist oder nicht, ist die Rekursionstechnik, die eine Funktion innerhalb einer Funktion verwendet, um zu prüfen, ob die Zahl ein perfektes Quadrat ist oder nicht.
- Obwohl die Rekursionstechnik schwierig zu verwenden ist, kann sie verwendet werden, um das Quadrat einer Zahl innerhalb weniger Codezeilen zu berechnen. Außerdem können wir mit Hilfe von Quadratzahlen viele Musterprogramme erzeugen. Wir können ein quadratisches Muster im Spiral- oder Zick-Zack-Format drucken. In ähnlicher Weise können die Quadratzahlen im Quellcode verwendet werden, um das Doppelquadrat zu erzeugen, beispielsweise die Nummer 16, bei der das Doppelquadrat die Nummer 2 ist.
Empfohlene Artikel
Dies ist eine Anleitung zu den Quadraten in Java. Hier haben wir die Einführung zusammen mit Beispielen und Codes für die Ausgabe von Quadraten in Java besprochen. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren.
- Muster in Java
- Spickzettel JavaScript
- Was ist eine Webanwendung?
- Arten von Web-Hosting
- Quadratwurzel in PHP
- Arrays in der Java-Programmierung
- Arbeits- und Top-3-Aufzählungsmethoden in C #
- Quadratwurzel in JavaScript