
Einführung in den DFS-Algorithmus
DFS ist als Depth First Search-Algorithmus bekannt, der die Schritte zum Durchlaufen jedes einzelnen Knotens eines Diagramms ohne Wiederholung eines Knotens bereitstellt. Dieser Algorithmus ist derselbe wie "Tiefenerster Durchlauf" für einen Baum, unterscheidet sich jedoch darin, einen Booleschen Wert zu verwalten, um zu überprüfen, ob der Knoten bereits besucht wurde oder nicht. Dies ist wichtig für das Durchlaufen von Diagrammen, da auch im Diagramm Zyklen vorhanden sind. In diesem Algorithmus wird ein Stapel verwaltet, um die angehaltenen Knoten während des Durchlaufs zu speichern. Der Name ist so, weil wir zuerst in die Tiefe jedes benachbarten Knotens fahren und dann einen anderen benachbarten Knoten weiter durchqueren.
Erläutern Sie den DFS-Algorithmus
Dieser Algorithmus widerspricht dem BFS-Algorithmus, bei dem alle benachbarten Knoten besucht werden, gefolgt von Nachbarn zu den benachbarten Knoten. Der Graph wird von einem Knoten aus untersucht und seine Tiefe wird vor dem Zurückverfolgen untersucht. Bei diesem Algorithmus werden zwei Dinge berücksichtigt:
- Aufrufen eines Scheitelpunkts: Auswahl eines Scheitelpunkts oder Knotens des Diagramms, der durchlaufen werden soll.
- Erkundung eines Scheitelpunkts: Durchqueren aller diesem Scheitelpunkt benachbarten Knoten.
Pseudocode für die Tiefensuche :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linear Traversal gibt es auch für DFS, die auf drei Arten implementiert werden können:
- Vorbestellung
- In Ordnung
- PostOrder
Reverse Postorder ist eine sehr nützliche Methode zum Durchlaufen und zur topologischen Sortierung sowie für verschiedene Analysen. Ein Stapel wird auch verwaltet, um die Knoten zu speichern, deren Erkundung noch aussteht.
Graph Traverse in DFS
In DFS werden die folgenden Schritte ausgeführt, um das Diagramm zu durchlaufen. Beginnen wir zum Beispiel bei einem gegebenen Graphen mit der Durchquerung von 1:
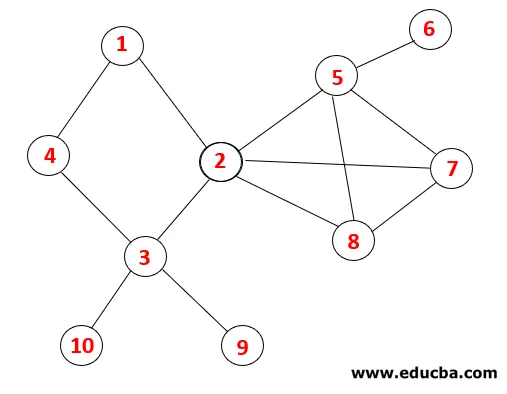
| Stapel | Traversalsequenz | Spanning Tree |
| 1 |  |
|
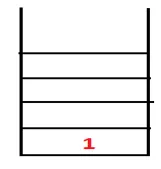 | 1, 4 |  |
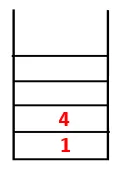 | 1, 4, 3 |  |
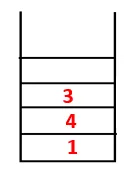 | 1, 4, 3, 10 | 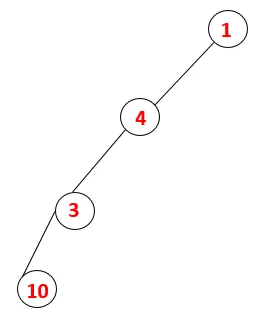 |
 | 1, 4, 3, 10, 9 | 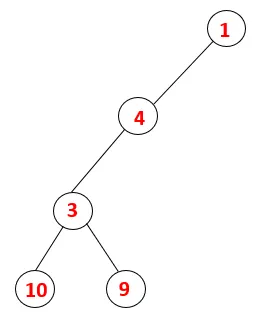 |
 | 1, 4, 3, 10, 9, 2 | 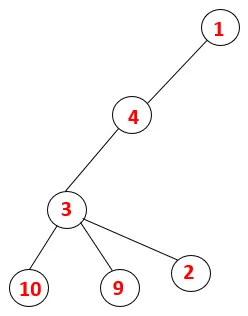 |
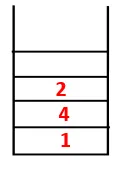 | 1, 4, 3, 10, 9, 2, 8 |  |
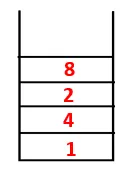 | 1, 4, 3, 10, 9, 2, 8, 7 | 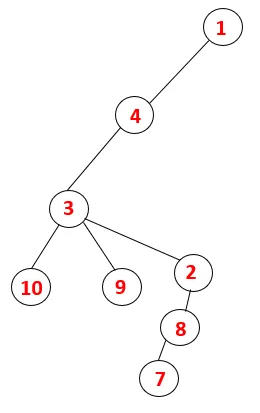 |
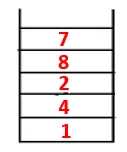 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
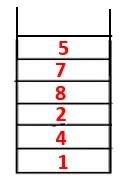 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 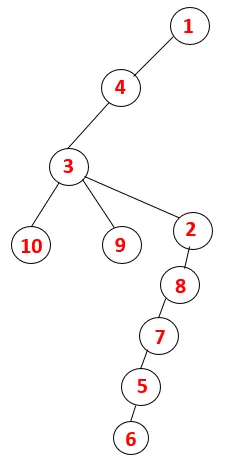 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 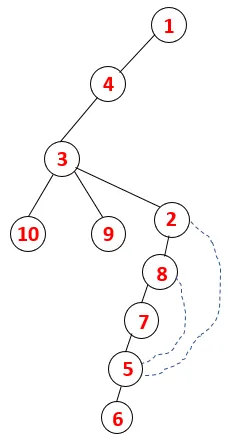 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
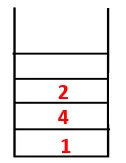 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 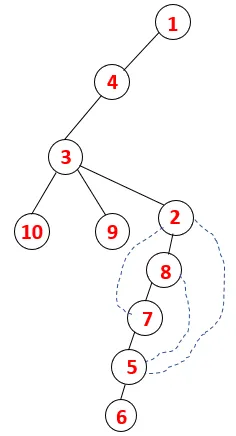 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 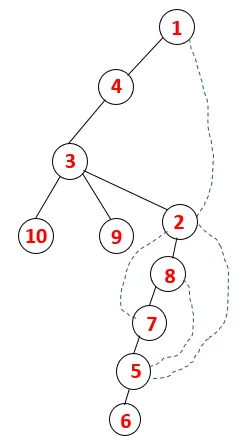 |
Erklärung zum DFS-Algorithmus
Im Folgenden sind die Schritte zum DFS-Algorithmus mit Vor- und Nachteilen aufgeführt:
Schritt 1 : Knoten 1 wird besucht und der Sequenz sowie dem Spanning Tree hinzugefügt.
Schritt 2: Benachbarte Knoten von 1 werden untersucht, dh 4, also 1 wird zum Stapel geschoben und 4 wird in die Sequenz sowie in den Spanning Tree geschoben.
Schritt 3: Einer der benachbarten Knoten von 4 wird erkundet und somit 4 auf den Stapel geschoben, und 3 gibt die Sequenz und den Spanning Tree ein.
Schritt 4: Benachbarte Knoten von 3 werden untersucht, indem man sie auf den Stapel schiebt und 10 in die Sequenz eingibt. Da es zu 10 keinen benachbarten Knoten gibt, springt 3 aus dem Stapel heraus.
Schritt 5: Ein weiterer benachbarter Knoten von 3 wird erkundet und 3 wird auf den Stapel geschoben und 9 wird besucht. Kein benachbarter Knoten von 9, also 3, wird herausgesprungen und der letzte benachbarte Knoten von 3, dh 2, wird besucht.
Ein ähnlicher Vorgang wird für alle Knoten ausgeführt, bis der Stapel leer wird, was die Stoppbedingung für den Durchquerungsalgorithmus anzeigt. - -> Gepunktete Linien im Spannbaum beziehen sich auf die im Diagramm vorhandenen hinteren Kanten.
Auf diese Weise werden alle Knoten im Diagramm durchlaufen, ohne einen der Knoten zu wiederholen.
Vorteile und Nachteile
- Vorteile: Der Speicherbedarf für diesen Algorithmus ist sehr viel geringer. Geringere räumliche und zeitliche Komplexität als BFS.
- Nachteile: Die Lösung ist nicht garantiert Anwendungen. Topologische Sortierung. Brücken des Graphen finden.
Beispiel zur Implementierung des DFS-Algorithmus
Unten sehen Sie das Beispiel zur Implementierung des DFS-Algorithmus:
Code:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Ausgabe:
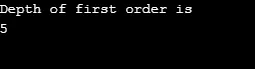
Erläuterung zum obigen Programm: Wir haben ein Diagramm mit 5 Eckpunkten (0, 1, 2, 3, 4) erstellt und ein besuchtes Array verwendet, um alle besuchten Eckpunkte zu verfolgen. Dann wird für jeden Knoten, dessen benachbarte Knoten existieren, derselbe Algorithmus wiederholt, bis alle Knoten besucht sind. Dann kehrt der Algorithmus zum aufrufenden Vertex zurück und nimmt ihn vom Stack.
Fazit
Der Speicherbedarf dieses Diagramms ist im Vergleich zu BFS geringer, da nur ein Stapel verwaltet werden muss. Als Ergebnis wird eine DFS-Spanning-Tree- und -Traversal-Sequenz generiert, die jedoch nicht konstant ist. Abhängig vom gewählten Startscheitelpunkt und Erkundungsscheitelpunkt ist eine Mehrfachdurchquerung möglich.
Empfohlene Artikel
Dies ist eine Anleitung zum DFS-Algorithmus. Hier diskutieren wir Schritt für Schritt Erklärungen, durchlaufen den Graphen in einem Tabellenformat mit Vor- und Nachteilen. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren -
- Was ist HDFS?
- Deep Learning-Algorithmen
- HDFS-Befehle
- SHA-Algorithmus