Einführung in den Zufallszahlengenerator in R
Der Zufallszahlengenerator in R ist ein wichtiger Aspekt der Datenwissenschaft, und Statistiken generieren Zufallszahlen oder generieren Zufallselemente. Wählen Sie beispielsweise zufällige Personen aus einem Populationsdatenrahmen aus, um die Daten zu analysieren und Einblicke in sie zu erhalten. Eine einfache Lösung, um Zufallszahlen zu generieren, ist die Verwendung von Funktionen. Zufallszahlen sind in verschiedenen Bereichen wie Modellierung, Datenwissenschaft und Stichproben (Statistik) nützlich. Mit der Erweiterung des Netzwerks erscheint die Entwicklung der Forschung in einem Zufallsgenerator notwendig. Zufallszahlen spielen eine Schlüsselrolle in Sicherheitssystemen und bieten uns ein ausgeklügeltes System, um die Sicherheit des Netzwerks zu erhöhen.
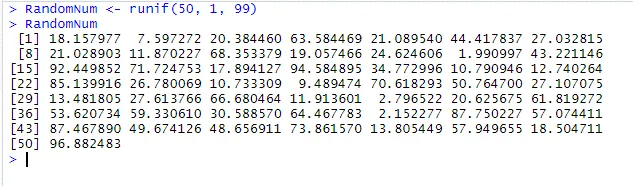
Im Folgenden finden Sie ein Beispiel zum Generieren und Drucken von 50 Werten zwischen 1 und 99 mithilfe der runif () -Funktion.
Code
RandomNum <- runif(50, 1, 99)
RandomNum
Ausgabe:
Ein Zufallszahlengenerator hilft dabei, eine Folge von Ziffern zu generieren, die als eine Funktion gespeichert werden können, die später in Operationen verwendet wird. Der Zufallszahlengenerator erzeugt keine Zufallswerte, da er einen Anfangswert namens SEED benötigt. Die Erzeugung von Zufallszahlen kann mit den Funktionen SET.SEED () gesteuert werden. Der Befehl SET.SEED () verwendet eine Ganzzahl, um die Zufallszahl der Generationen zu starten. Ferner kann die erzeugte Zufallszahlenfolge gespeichert und später verwendet werden.
Beispiel: Mit dem Code werden 10 Zahlen zwischen 1 und 100 abgetastet und einige Male wiederholt.
Zum ersten Mal startet SET.SEED () bei Start als 5 und zum zweiten Mal als Start als 12. Für jede Iteration wurden zehn Zufallszahlen generiert.
Code
set.seed(5) # random number will generate from 5
TenRandomNumbers <- sort(sample.int(100, 10))
TenRandomNumbers
Ausgabe:
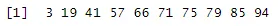
Code:
set.seed(12) # random number will generate from 12
TenRandomNumbers <- sort(sample.int(100, 10))
TenRandomNumbers
Ausgabe:
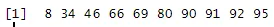
Zufallszahlengenerator-Funktionen
Es gibt in R eingebaute Funktionen, um eine Reihe von Zufallszahlen aus Standardverteilungen wie Normal-, Uniform-, Binomialverteilungen usw. zu generieren. Im nächsten Abschnitt sehen wir verschiedene Funktionen wie runif (), rnorm (), rbinom () und rexp (), um Zufallszahlen zu generieren.
1. Gleichmäßig verteilte Zufallszahlen
Zur Erzeugung gleichmäßig verteilter Zufallszahlen wird runif () verwendet. Standardbereich 0 - 1. Zunächst müssen Sie die Anzahl angeben, die generiert werden soll. Zusätzlich kann der Bereich der Verteilung mit den Argumenten max und min angegeben werden.
Code
# To get 5 uniformly distributed Random Numbers
runif(5)
Ausgabe:
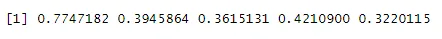
Code
# Get 5 random Numbers from 5 to 99
runif(5, min=5, max=99)
Ausgabe:
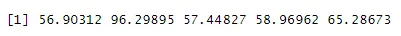
Code
#To generate 5 integers from 0 to 100
floor(runif(5, min=0, max=101))
Ausgabe:
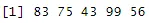
Code
# Generating integers without replacement
sample(1:100, 5, replace=FALSE)
Ausgabe:
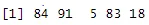
2. Normalverteilte Zufallszahlen
Um Zahlen aus einer Normalverteilung zu generieren, wird rnorm () verwendet. Wenn der Mittelwert 0 und die Standardabweichung 1 ist, müssen Sie zunächst die Anzahl angeben, die generiert werden soll. Zusätzlich können Mittelwert und SD (Standardabweichung) als Argumente angegeben werden.
Code
rnorm(5)
Ausgabe:
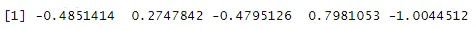
Code
# using a different mean and standard deviation
rnorm(4, mean=70, sd=10)
Ausgabe:
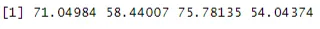
Code
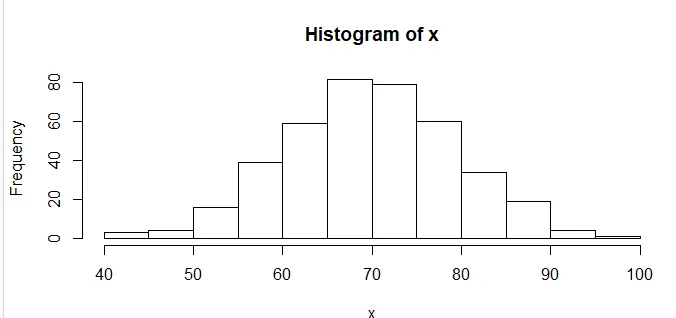
# histogram of the numbers to verify the distribution
X <- rnorm(400, mean=70, sd=10)
hist(X)
Ausgabe:
Verwenden von rnorm () zum Generieren einer normalverteilten Zufallszahl
3. Binomiale Zufallszahlen
Die binomischen Zufallszahlen sind eine diskrete Menge von Zufallszahlen. Um eine Binomialzahl abzuleiten, wird der Wert von n in die gewünschte Anzahl von Versuchen geändert. Zum Beispiel Versuch 5, wobei n = 5 ist
Code:
n= 5
p=.5
rbinom(1, n, p)
# 1 success in 5 trails
n= 5
p=.5
rbinom(19, n, p) # 10 binomial numbers
Ausgabe:
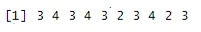
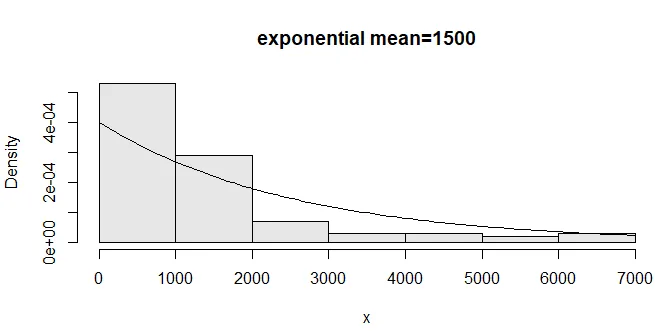
4. Exponentiell verteilte Zufallszahlen
Die Exponentialverteilung wird verwendet, um die Lebensdauer elektrischer Komponenten zu beschreiben. Beispielsweise beträgt die durchschnittliche Lebensdauer einer elektrischen Lampe 1500 Stunden.
Code:
x=rexp(100, 1/1500)
hist(x, probability=TRUE, col= gray(.9), main="exponential mean=1500")
curve(dexp(x, 1/1500), add= T)
Ausgabe:
Ganzzahl und Gleitkommazahl generieren
Nun lernen wir, Zufallszahlen für zwei Arten von Zahlen zu generieren, die in R verfügbar sind. Es handelt sich um Ganzzahlen und Gleitkomma- oder Gleitkommazahlen. R erkennt die beiden Kategorien automatisch und wechselt sie bei Bedarf. Eine ganze Zahl in R besteht aus der ganzen Zahl, die positiv oder negativ sein kann, während eine Gleitkommazahl reelle Zahlen enthält. Es besteht aus einem Wert, der die hinter dem Komma liegende Ziffer angibt. Der Wert ist binär und die Angabe der Anzahl der zu überfahrenden binären Stellen ist verfügbar. Die in sample () integrierte Funktion zur Generierung von Zufallszahlen ist zuverlässig und schnell. Für die geschäftlichen Anforderungen müssen Sie eine Datenstichprobe analysieren. Zur Auswahl eines Samples hat R die Funktion sample (). Um zufällige ganze Zahlen zwischen 5 und 20 darunter zu generieren, wird der Beispielfunktionscode verwendet.
Code
rn = sample(5:20, 5)
rn
Ausgabe:
Generierung einer Zufallsstichprobe von 5
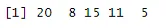
Im obigen Beispiel wurden fünf Werte als das angegebene Argument generiert. Wir haben gesehen, wie eine Teilmenge von Zufallswerten in R ausgewählt werden kann. In Echtzeit müssen Sie eine Zufallsstichprobe aus einem vorhandenen Datenrahmen generieren. Die Auswahl einer Stichprobe von Daten zur Beobachtung aus einem großen Datensatz ist eine der Aufgaben, die Dateningenieure in ihrem täglichen Leben übernehmen.
Code
Height_Weight_Data <- read.csv("test.csv") # to test this please download csv file
Height_Weight_Data
# Height_Weight_Data sample data frame; selecting a random subset in r
Sample <- Height_Weight_Data(sample(nrow(Height_Weight_Data), 5), ) # pick 5 random rows from dataset
Sample
Ausgabe:
Generieren einer Zufallsstichprobe aus Datenrahmennamen als Height_Weight_Data

Einige Dinge, an die man sich in Bezug auf Gleitkommazahlen erinnern muss.
- Sie sind von Natur aus binär.
- Limitiert in den dargestellten reellen Zahlen.
Nun wollen wir sehen, wie zufällige Gleitzahlen zwischen -10 und 10 generiert werden können
Code
Random <- runif(n=10, min=-10, max=10)
Random
Ausgabe:
Generieren zufälliger Gleitkommazahlen

Runif () bezieht sich auf die zufällige Uniform. Im obigen Beispiel haben wir 10 zufällig verteilte Zahlen zwischen (-10: 10) abgeleitet.
Fazit
In diesem Artikel haben wir den Zufallszahlengenerator in R besprochen und gesehen, wie die SET.SEED-Funktion zum Steuern der Zufallszahlengenerierung verwendet wird. Wir haben gesehen, wie SEED für reproduzierbare Zufallszahlen verwendet werden kann, die in der Lage sind, eine Folge von Zufallszahlen zu erzeugen und mit SET.SEED () einen Zufallszahlengenerator einzurichten. Die statistische Methode, die die Erzeugung von Zufallszahlen erfordert, wird gelegentlich während der Analyse verwendet. R ist mit mehreren Funktionen ausgestattet, z. B. Uniform, Normal, Binomial, Poisson, Exponential und Gamma-Funktion, mit denen die häufigste Wahrscheinlichkeitsverteilung simuliert werden kann.
Empfohlene Artikel
Dies ist eine Anleitung zum Zufallszahlengenerator in R. Hier diskutieren wir die Einführung und Funktionen des Zufallszahlengenerators in R zusammen mit dem entsprechenden Beispiel. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren -
- Lineare Regression in R
- Binomialverteilung in R
- Logistische Regression in R
- Liniendiagramm in R
- Anleitung zum Zufallszahlengenerator in Python
- Zufallszahlengenerator in C #
- Zufallszahlengenerator in PHP