Einführung in die Heap-Sortierung in C
Das Sortieren ist eine Technik, bei der es um das Sortieren von Elementen anhand verschiedener Eigenschaften geht. (Eigenschaften wie Daten in aufsteigender, absteigender oder alphabetischer Reihenfolge anordnen). Ein wichtiges Beispiel für das Sortieren, an das wir hier denken können, ist das Bestellen von Artikeln beim Online-Einkauf. Wir können uns auf die Preise, die Popularität, das Neueste und so weiter beziehen. Es gibt also viele Techniken zum Positionieren von Elementen durch Sortieren. In diesem Thema erfahren Sie mehr über die Heap-Sortierung in C.
Hier lernen wir eine der gebräuchlichsten Sortiertechniken, Heap Sort, über die Programmiersprache C.
Die Logik für die Heap-Sortierung
Wie können wir tatsächlich eine Heap-Sortierung durchführen? Schauen wir uns das unten an.
Erstens ist der Heap eine der baumbasierten Datenstrukturen. Der Baum, um den es hier geht, ist immer ein vollständiger Binärbaum. Und es gibt zwei Arten von Haufen
- Min - Heap: Im Allgemeinen in aufsteigender Reihenfolge angeordnet, dh, wenn das übergeordnete Knotenelement einen Wert aufweist, der kleiner als der der untergeordneten Knotenelemente ist.
- Max - Heap: Im Allgemeinen in absteigender Reihenfolge angeordnet, dh, wenn das übergeordnete Knotenelement einen höheren Wert als das untergeordnete Knotenelement aufweist.
Schritte für die Heap-Sortierung
- Sobald unsortierte Listendaten erhalten wurden, werden Elemente in der Heap-Datenstruktur entweder basierend auf der Erstellung eines Min-Heaps oder eines Max-Heaps organisiert.
- Das erste Element aus der obigen Liste wird unserem Array hinzugefügt
- Wieder wird die Kopfdatenstrukturtechnik wie im ersten Schritt gebildet, und wieder wird entweder das höchste Element oder das niedrigste Element aufgenommen und in unser Array aufgenommen.
- Wiederholte Schritte helfen uns, das Array mit der sortierten Liste zu erhalten.
Programm für die Heap-Sortierung in C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Zuerst bitten wir den Benutzer, die Anzahl der Elemente einzugeben, die zum Sortieren herangezogen werden, und dann darf der Benutzer verschiedene Elemente eingeben, die sortiert werden sollen.
Schritte gefolgt
- Als Nächstes konzentrieren wir uns auf die Erstellung eines Heap-Arrays, in diesem Fall eines Max-Heap-Arrays.
- Die Hauptbedingung für das Abrufen eines max-heap-Arrays besteht darin, zu überprüfen, ob kein übergeordneter Knotenwert kleiner als sein untergeordneter Knotenwert ist. Wir werden tauschen, bis wir diese Bedingung erreichen.
- Der Hauptvorteil dieses vollständigen Binärbaums besteht darin, dass auf den linken und rechten Kindknoten eines Elternknotens mit den Werten 2 (i) + 1 bzw. 2 * (i) + 2 zugegriffen werden kann. Wobei ich der übergeordnete Knoten ist.
- Auf diese Weise platzieren wir unseren Wurzelknoten, der den Maximalwert enthält, ganz rechts im Blattknoten. Und dann wieder auf die gleiche Weise vorgehen, so dass die nächste maximale Anzahl zum Wurzelknoten wird.
- Wir werden auf die gleiche Weise vorgehen, bis nur noch ein Knoten im Heap-Array vorhanden ist.
- Und dann ordnen wir unser Heap-Array in aufsteigender Reihenfolge zu einem perfekt sortierten Array an.
- Schließlich drucken wir das sortierte Array in der Ausgabe.
Ausgabe:
Die Ausgabe ist unten angefügt.
Lassen Sie mich Ihnen die bildliche Darstellung der Ereignisse zeigen:
- Die eingegebenen Daten werden zunächst wie folgt in Form eines eindimensionalen Arrays dargestellt.

- Die bildliche Darstellung des gebildeten Binärbaums sieht wie folgt aus:
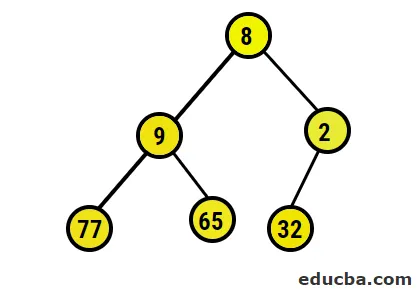
- Jetzt werden wir in den maximalen Heap konvertieren, indem wir sicherstellen, dass alle übergeordneten Knoten immer größer als untergeordnete Knoten sind. Wie in der Ausgabe unter Heap Sorted Array erwähnt, wäre die bildliche Darstellung:
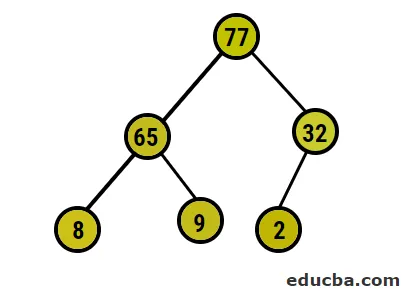
- Danach werden wir den Wurzelknoten mit dem äußersten Blattknoten tauschen und ihn dann aus dem Baum löschen. Der Blattknoten ist ab und zu die Wurzel. Dann wird derselbe Prozess ausgeführt, um wieder das höchste Element in der Wurzel zu erhalten
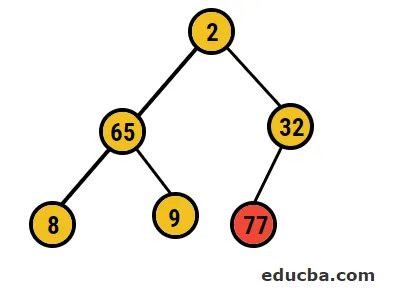
- In diesem Fall werden also 77 Ziffern aus diesem Baum gelöscht und in unser sortiertes Array eingefügt, und der Vorgang wird wiederholt.
Das obige haben wir für die Bildung von Max-Heap-Array gesehen. Der gleiche Prozess wird auch mit der Min-Heap-Array-Bildung behandelt. Wie oben erläutert, besteht der einzige Unterschied in der Beziehung zwischen übergeordneten und untergeordneten Knotenelementen.
Können Sie als Übung versuchen, die Heap-Sortierung in absteigender Reihenfolge zu bilden?
Fazit
Obwohl es viele Sortiertechniken gibt, wird die Haufensortierung aufgrund ihrer zeitlichen und räumlichen Komplexität als eine der besseren Sortiertechniken angesehen. Die Zeitkomplexität für alle besten, durchschnittlichen und schlechtesten Fälle ist O (nlogn), wobei die Komplexität im schlechtesten Fall besser ist als die Komplexität im schlechtesten Fall von Quicksort, und die Raumkomplexität ist O (1).
Empfohlene Artikel
Dies ist eine Anleitung zur Heap-Sortierung in C. Hier diskutieren wir die Logik und die Schritte für die Heap-Sortierung mit dem Beispielcode und der Ausgabe zusammen mit bildlichen Darstellungen. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Heap-Sortierung in Java
- Auswahl Sortieren in Java
- Palindrom im C-Programm
- Muster in der C-Programmierung
- Heap-Sortierung in C ++ (Algorithmus)
- Heap-Sortierung in Python
- C Programmieren der Matrixmultiplikation