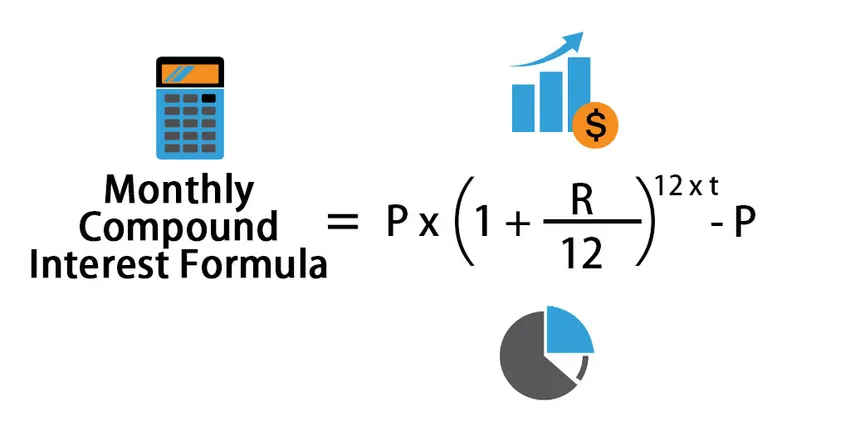
Monatliche Zinseszinsformel (Inhaltsverzeichnis)
- Formel
- Beispiele
- Taschenrechner
Was ist die monatliche Zinseszinsformel?
Wenn ein bestimmter Geldbetrag für eine bestimmte Dauer ausgeliehen wird und ein zusätzlicher Betrag zusammen mit dem ausgeliehenen Betrag separat gezahlt werden muss. Dann wird der zusätzliche Betrag, den wir zum Festpreis zahlen, als Zins bezeichnet. Zinseszins ist der Gesamtzins, der den ursprünglichen Zins und den Zins des neuen Kapitals umfasst, der sich aus der Aufzinsung des ursprünglichen Kapitals ergibt. Für monatliche Zinseszinsberechnung wird der Zins berechnet, der den ganzen Monat im ganzen Jahr berechnet wird.
Die monatliche Zinseszinsformel kann wie folgt berechnet werden:
Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P
wo,
- P = Hauptbetrag
- R = Rate
- t = Zeit
Beispiele für monatliche Zinseszinsformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des monatlichen Zinseszinses besser zu verstehen.
Sie können diese Excel-Vorlage für monatliche Zinseszinsformeln hier herunterladen - Excel-Vorlage für monatliche ZinseszinsformelnMonatliche Zinseszinsformel - Beispiel 1
Ein Kreditnehmer hat eine Summe von 10.000 Rupien zu einem Zinssatz von 8% geliehen. Berechnen Sie den monatlichen Zinseszins für 2 Jahre?
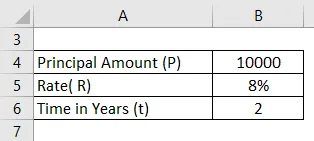
Lösung:
Die monatlichen Zinseszinsen werden nach der unten angegebenen Formel berechnet
Monatlicher Zinseszins = P * (1 + (R / 12)) 12 * t - P
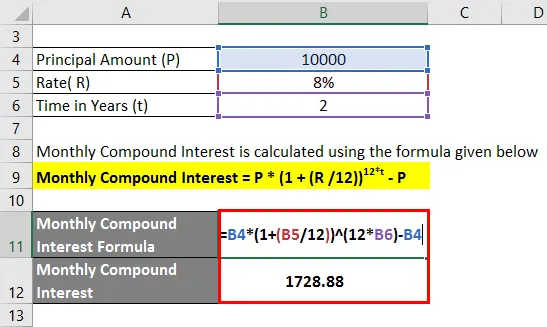
- Monatlicher Zinseszins = 10.000 (1 + (8/12)) 2 * 12 - 10.000
- Monatlicher Zinseszins = 1.728, 88
Der monatliche Zinseszins für 2 Jahre beträgt Rs 1.728, 88
Monatliche Zinseszinsformel - Beispiel 2
Eine Geldsumme, die mit einer Rate von 10% angelegt wird, ist Rs 20.000. Was wird der monatliche Zinseszins für die 10 Jahre sein?

Lösung:
Die monatlichen Zinseszinsen werden nach der unten angegebenen Formel berechnet
Monatlicher Zinseszins = P * (1 + (R / 12)) 12 * t - P
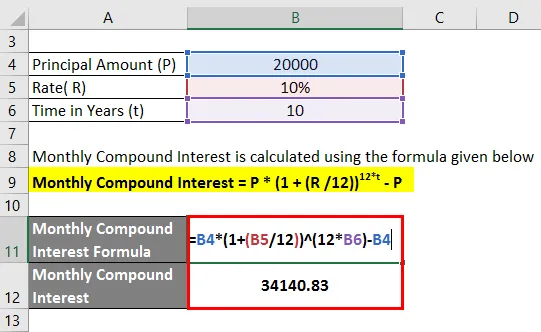
- Monatlicher Zinseszins = 20.000 (1 + 10/12)) 10 * 12 - 20.000
- Monatlicher Zinseszins = 34.140, 83
Der monatliche Zinseszins für 10 Jahre beträgt Rs 34.140, 83
Monatliche Zinseszinsformel - Beispiel 3
Mrs. Jefferson kaufte einen Antiquitätenstatus für 500 Dollar. Fünf Jahre später verkaufte sie diesen Status für 800 Dollar. Sie betrachtete es als Teil der Investition. Berechnen Sie die jährliche Rate, die sie erhielt?
Lösung:
Wenn wir eine Investition von 500 USD in Betracht ziehen und in der Zukunft nach t = 10 Jahren 800 USD verdienen. Wir nehmen eine Jahresrate m = 1 an und implementieren sie in die Formel.
A = P (1 + r / m) mt
- 800 = 500 (1+ r / 1) 1 · 10
- 800 = 500 (1 + r) 10
Nun lösen wir in den folgenden Schritten nach der Rate (r).
- 800 = 500 (1 + r) 10
- 8/5 = (1 + r) 10
Nun nehmen wir die Potenz von (1/10) auf der linken Seite der Gleichung und löschen von der rechten Seite.
- (8/5) 1/10) = 1 + r
Berechnen Sie den Wert links und lösen Sie nach r.
- 1, 0481 = 1 + r
- 1, 0481-1 = r
- 0, 0481 = r
Frau Jefferson verdiente jedoch den jährlichen Zinssatz von 4, 81%, was keine schlechte Rendite darstellt.
Erläuterung
Zinseszins ist das Produkt aus dem anfänglichen Nennbetrag um eins plus dem jährlichen Zinssatz, der auf die Anzahl der Zinsperioden minus eins erhöht wurde. Der ursprüngliche Darlehensbetrag wird dann vom resultierenden Wert abgezogen.
Der Zinseszins kann wie folgt berechnet werden:
Zinseszinsformel = (P (1 + i) n ) - P
Zinseszinsformel = (P (1 + i) n - 1)
Wo:
- P = Hauptbetrag
- i = jährlicher Zinssatz in Prozent
- n = Zinsperioden
Es gibt eine Reihe von Verfahren, mit denen wir den monatlichen Zinseszins berechnen können.
Schritt 1: Wir müssen den Zinsbetrag berechnen, der durch die Verwendung von monatlichen Zinseszinsen erzielt wird. Die Formel kann wie folgt berechnet werden:
- A = (P (1 + i) n - 1) - P
Schritt 2: Wenn wir davon ausgehen, dass der Zinssatz 5% pro Jahr beträgt. Zunächst müssen wir den Zinssatz in der entsprechenden Dezimalzahl ausdrücken. Dies kann auf folgende Weise erfolgen.
- 5% = 5/100 = 0, 05
Schritt 3: Da wir wissen, dass die Zinsen monatlich berechnet werden, können wir n = 12 nehmen. In diesem Fall wird jedoch der Zeitraum angegeben, und wir gehen davon aus, dass das Darlehen für einen Zeitraum von einem Jahr aufgenommen wird. Jetzt haben wir alle Variablen zur Verfügung, die wir direkt in die Formel einsetzen und daraus das Ergebnis erhalten können.
- A = 1000 ((1 + 0, 05 / 12) 12-1 )
- A = 1000 ((1 + 0, 0042) 12-1)
- A = 1000 ((1, 0042) 12-1)
- A = 1000 (1, 0516-1)
- A = 1000 (0, 0516)
- A = 51, 6
Wir haben den Zinssatz für 1 Jahr durch monatliche Aufzinsung mit ca. 51, 6 berechnet
Monatliche Zinseszinsen spiegeln keine spürbaren Veränderungen wider, wenn wir einen bestimmten Geldbetrag für eine kurzfristige Laufzeit parken. Der Grund dafür ist, dass es mehrere Jahre dauert, bis das Compoundieren spürbare Änderungen bewirkt.
Das Wichtigste am Zinseszins ist, dass Ihre Investitionen schneller wachsen als bei einfachen Zinsen. Je häufiger Ihr Zinseszinsintervall ist, desto größer ist die Differenz, oder wir können sagen, dass die täglichen Zinseszinserträge aus Ihren Anlagen höher sind als die jährlichen Zinseszinserträge für einen bestimmten Zinssatz.
Die folgende Tabelle zeigt den Unterschied, den die Anzahl der Zinsperioden über einen bestimmten Zeitraum für ein Darlehen in Höhe von 10.000 USD mit einem jährlichen Zinssatz von 10% über einen Zeitraum von 12 Jahren ausmachen kann.
| Verbindungsfrequenz | Anzahl der Compoundierungsperioden | Werte für i und n | Gesamtzins |
| Jährlich | 1 | I = 10%, n = 12 | 21.384, 2837 US-Dollar |
| Halbjährlich | 2 | I = 5%, n = 24 | 22.250, 9994 US-Dollar |
| Vierteljährlich | 4 | I = 2, 5%, n = 48 | 22.714, 8956 USD |
| Monatlich | 12 | I = 0, 833%, n = 144 | 23.036, 4896 US-Dollar |
Relevanz und Verwendung der monatlichen Zinseszinsformel
Zinseszinsen haben sich als das bessere Instrument für Investitionen erwiesen, aber es kann sehr gefährlich sein, wenn es auf Ihren Darlehensbetrag anwendbar ist. Am Ende zahlen Sie mehr Zinsen für Ihren Darlehensbetrag.
Die Aufzinsung wird effektiver, wenn Ihre Investition entweder monatlich oder vierteljährlich statt jährlich erfolgt, da sie eine bessere Rendite erzielt. Wenn Sie Geld von einer Bank oder einem Finanzinstitut leihen, ist eine jährliche Aufzinsung die beste Option. Wenn Sie einen bestimmten Geldbetrag verleihen, ist die tägliche Aufzinsung produktiver. Wir sollten jedoch bedenken, dass die Aufzinsung je nach den Umständen günstig oder ungünstig sein kann.
Zinseszinsen sorgen für eine bessere Rendite Ihrer Investition, abhängig von der Laufzeit und dem Umfang der Investition. Zinseszinsen steigen schneller als erwartet.
Die Vorteile von Zinseszinsen sind nachfolgend aufgeführt:
- Reinvestition
- Bessere Rendite für Ihre Investition.
- Langfristige Einsparungen.
- Erhöhtes Einkommen.
Monatlicher Zinseszins-Formelrechner
Sie können den folgenden Formelrechner für monatliche Zinseszinsen verwenden
| P | |
| R | |
| t | |
| Monatliche Zinseszinsformel | |
| Monatliche Zinseszinsformel = | P x ((1 + R / 12) 12 * t - P) |
| = | 0 x ((1 +0/12) 12 * 0 - 0) = 0 |
Empfohlene Artikel
Dies ist eine Anleitung zur monatlichen Zinseszinsformel. Hier besprechen wir die Berechnung der monatlichen Zinseszinsformel zusammen mit praktischen Beispielen. Wir bieten auch einen monatlichen Zinsrechner mit einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Formel für die durchschnittliche jährliche Wachstumsrate
- Wie berechnet man den Nominalzins?
- Tägliche Zinseszinsformel
- Leitfaden zur Poisson-Verteilungsformel
- Zins vs Dividende | Die acht wichtigsten Unterschiede, die Sie kennen sollten