Einführung in AVL Tree in Data Structure
Der AVL-Baum in der Datenstruktur bezieht sich auf den Adelson-, Velski- und Landis-Baum. Dies ist eine erweiterte Version des binären Suchbaums. Ab dem binären Suchbaum weist es alle Funktionen auf, unterscheidet sich jedoch nur dadurch, dass sie einen Unterschied zwischen der Höhe des linken Unterbaums und des rechten Unterbaums aufrechterhalten. Außerdem wird sichergestellt, dass sein Wert im Baum <= 1 ist. Dies wird als Balance bezeichnet Faktor.
Balance Factor = height(left-subtree) − height(right-subtree)
Zum Beispiel: Betrachten Sie die folgenden Bäume

Im obigen Beispiel wird die Höhe des rechten Unterbaums = 2 und des linken = 3, also BF = 2, dh <= 1, also Baum als ausgeglichen bezeichnet.
Warum brauchen wir einen AVL-Baum in DS?
Während der Arbeit mit dem binären Suchbaum stoßen wir auf ein Szenario, in dem die Elemente in sortierter Reihenfolge vorliegen. In solchen Fällen sind alle Elemente des Arrays auf einer Seite der Wurzel angeordnet. Dies führt zu einer Zunahme der Zeitkomplexität beim Suchen eines Elements in einem Array, und die Komplexität wird zu -O (n), dh der Komplexität des Baums im ungünstigsten Fall . Um solche Probleme zu lösen und die Suchzeit zu verkürzen, wurden AVL-Bäume von Adelson, Velski & Landis erfunden.
Beispiel:

In der obigen Abbildung war die Höhe des linken Teilbaums = 3 wie folgt
Höhe des rechten Teilbaums = 0
Somit ist Balance Factor = 3-0 = 3. Die Suche nach einem Element in einem solchen Baum hat also eine Komplexität von 0 (n), die der linearen Suche ähnlich ist. Um diese komplexe Suche zu vermeiden, wurde ein AVL-Baum eingeführt, bei dem jeder Knoten im Baum gepflegt werden muss
balance factor <= 1, andernfalls müssen verschiedene Rotationstechniken durchgeführt werden, um einen solchen Baum auszugleichen.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Arten von Rotationen
Wenn der Ausgleichsfaktor für den Baum die Bedingung <= 1 nicht erfüllt, müssen Rotationen an ihnen durchgeführt werden, um ihn in einen ausgeglichenen Baum zu verwandeln.
Es gibt 4 Arten von Rotationen:
1. Linksrotation: Wenn das Hinzufügen eines Knotens rechts vom Baum zu einem Ungleichgewicht führt, muss in diesem Fall eine Linksrotation durchgeführt werden.
2. Rechtsdrehung: Wenn das Hinzufügen eines Knotens links vom Baum zu einem Ungleichgewicht des Knotens führt, muss eine Rechtsdrehung ausgeführt werden. Mit anderen Worten, wenn die Anzahl der Knoten auf der linken Seite zunimmt, entsteht die Notwendigkeit, die Elemente auf die rechte Seite zu verschieben, um sie auszugleichen, so dass es sich um eine Rechtsdrehung handelt.
3. Links-Rechts-Drehung: Diese Art der Drehung ist eine Kombination der oben erläuterten 2 Drehungen. Diese Art der Drehung tritt auf, wenn ein Element zum rechten Teilbaum eines linken Baums hinzugefügt wird.
Führen Sie in einem solchen Fall zuerst eine Linksdrehung auf dem Teilbaum aus, gefolgt von einer Rechtsdrehung des linken Baums.
4. Rechts-Links-Drehung: Diese Art der Drehung setzt sich ebenfalls aus einer Folge von mehr als 2 Umdrehungen zusammen. Diese Art der Drehung ist erforderlich, wenn ein Element links vom rechten Teilbaum hinzugefügt wird und der Baum ein Ungleichgewicht aufweist. In einem solchen Fall führen wir zuerst eine Rechtsdrehung auf dem rechten Teilbaum und dann eine Linksdrehung auf dem rechten Baum durch.
Operationen auf dem AVL-Baum in DS
Unterhalb von 3 Vorgängen, die im AVL-Baum ausgeführt werden können:
1. Suche
Diese Operation ähnelt der Durchführung einer Suche im binären Suchbaum. Es werden folgende Schritte ausgeführt:
- Lesen Sie das vom Benutzer bereitgestellte Element mit x.
- Vergleichen Sie das Element vom Stamm aus. Wenn es dasselbe ist, fahren Sie mit dem nächsten Schritt fort.
- Wenn x
Ansonsten gehe zum richtigen Kind und vergleiche noch einmal.
Befolgen Sie die Schritte B und C, bis Sie das Element gefunden und beendet haben.
Dieser Prozess hat eine O (log n) -Komplexität.
Beispiel:
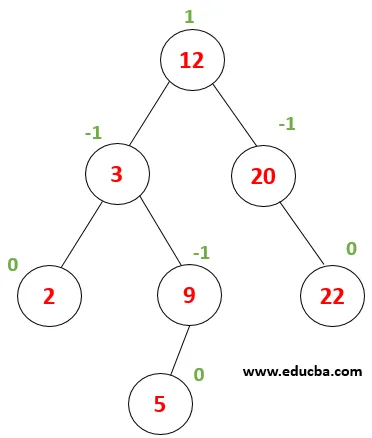 | Betrachten Sie diesen Baum, in dem eine Suche nach dem Knotenwert 9 durchgeführt werden muss. Lassen Sie zuerst x = 9, Wurzelwert (12)> x, dann muss der Wert im linken Teilbaum des Wurzelelements stehen. |
 | Nun wird x mit dem Knotenwert 3 verglichen x> 3 also müssen wir uns dem richtigen Unterbaum nähern. |
 | Jetzt wird x mit Knoten (9) verglichen, wobei 9 == 9 true zurückgibt. Somit ist die Elementsuche im Baum abgeschlossen. |
2. Einfügen
Wenn Sie ein Element in den AVL-Baum einfügen, müssen Sie die Position des Elements ermitteln, das eingefügt werden soll. Anschließend wird das Element wie beim Einfügen in BST angehängt. Anschließend wird jedoch überprüft, ob der Baum noch ausgeglichen ist oder nicht dh der Balance-Faktor eines Knotens ist <= 1. Und bestimmte Drehungen werden nach Bedarf durchgeführt.
Die Komplexität ist O (log n).
Beispiel: Betrachten Sie den folgenden Baum,
 | Jeder Knoten hat einen Ausgleichsfaktor von 0, -1 oder 1, sodass der Baum ausgeglichen ist. Lassen Sie uns nun wissen, was passiert, wenn ein Knoten mit dem Wert 1 eingefügt wird. Der erste Baum wird durchlaufen, um den Ort zu finden, an dem er eingefügt werden muss… 1 <2 wird somit als linkes Kind des Knotens (2) geschrieben. |
 | Nach dem Einsetzen wird der Knoten (9) mit einem Ausgleichsfaktor = 2 aus dem Gleichgewicht gebracht. Jetzt wird er einer Rechtsdrehung unterzogen. |
 | Ein Baum wird nach der Rechtsdrehung ausgeglichen und der Einfügevorgang ist somit erfolgreich abgeschlossen. |
3. Löschung
Das Löschen eines Elements in der AVL-Struktur umfasst auch das Suchen und anschließende Löschen eines Elements in der Struktur. Der Suchvorgang ist derselbe wie bei BST. Nach dem Auffinden des zu löschenden Elements wird das Element aus dem Baum entfernt und die Elemente werden so angepasst, dass es wieder BST wird. Nachdem überprüft wurde, ob diese Elemente einen Ausgleichsfaktor von 0, -1 oder 1 haben, werden geeignete Rotationen durchgeführt, um sie auszugleichen.
Komplexität wenn O (log n).
 | Betrachten Sie den gegebenen Baum, dessen alle einen Gleichgewichtsfaktor von 0, -1 oder 1 haben. Löschen wir nun einen Knoten mit dem Wert 16. Der erste Baum wird durchlaufen, um den Knoten mit dem Wert 16 zu finden, der mit einem Suchalgorithmus identisch ist. |
 | Knoten 16 wird durch den inorder-Vorgänger dieses Knotens ersetzt, der das größte Element aus dem linken Teilbaum ist, dh 12 Der Baum ist aus dem Gleichgewicht geraten, daher muss eine LL-Rotation durchgeführt werden. |
 | Jetzt ist jeder Knoten ausgeglichen. |
Schlussfolgerung - AVL-Baum in der Datenstruktur
Der AVL-Baum ist ein Abkömmling des binären Suchbaums, überwindet jedoch den Nachteil der zunehmenden Komplexität, wenn die Elemente sortiert werden. Es überwacht den Ausgleichsfaktor des Baums auf 0 oder 1 oder -1. Wenn der Baum aus dem Gleichgewicht gerät, werden entsprechende Rotationstechniken durchgeführt, um den Baum auszugleichen.
Empfohlene Artikel
Dies ist eine Anleitung zu AVL Tree in Data Structure. Hier diskutieren wir die Einführung, Operationen am AVL-Baum in DS und Arten von Rotationen. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren.
- jQuery Elements
- Was ist Data Science?
- Baumarten in der Datenstruktur
- C # -Datentypen