Populationsabweichungsformel (Inhaltsverzeichnis)
- Populationsabweichungsformel
- Beispiele für Populationsabweichungsformeln (mit Excel-Vorlage)
Populationsabweichungsformel
In der Statistik ist eine Varianz grundsätzlich ein Maß für die Streuung der Datensatzwerte vom Mittelwert des Datensatzes. Es misst die Entfernung dieses Datenpunktes und den Mittelwert. Je höher die Varianz, desto höher ist die Streuung, und die Datenpunkte sind zu weit vom Mittelwert entfernt. In ähnlicher Weise zeigt eine geringere Varianz an, dass die Datenpunkte näher am Mittelwert liegen. Es ist sehr nützlich, um Datensätze zu vergleichen, die den gleichen Mittelwert, aber einen anderen Bereich haben können. Populationsvarianz gibt in demselben Sinne an, wie die Populationsdatenpunkte verteilt sind. Dies ist der Durchschnitt der Abstände von jedem Datenpunkt in der Grundgesamtheit zum Mittelwert im Quadrat. Berechnen Sie normalerweise die Varianz der Bevölkerungsdaten, aber manchmal sind die Bevölkerungsdaten so groß, dass es wirtschaftlich nicht sinnvoll ist, die Varianz dafür zu finden. In diesem Fall wird die Stichprobenvarianz berechnet und diese wird zum Repräsentanten der Populationsvarianz.
Angenommen, Sie haben einen Populationsdatensatz X mit den Datenpunkten (X1, X2 …… ..Xn). Die Formel für die Populationsvarianz ist gegeben durch:
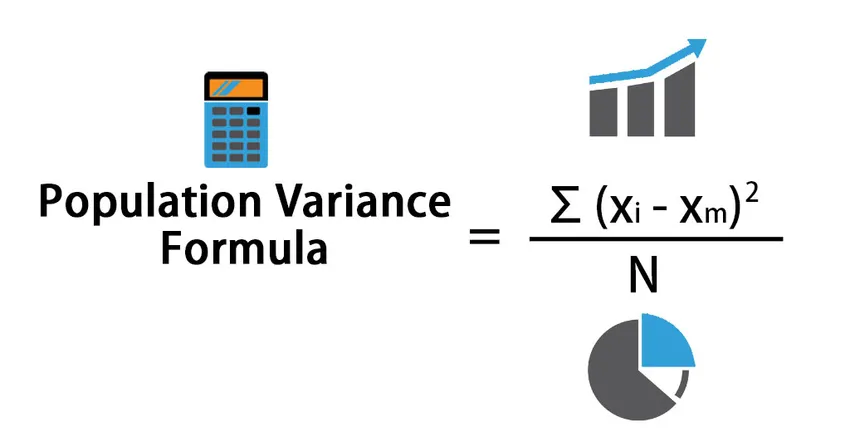
Population Variance = Σ (X i – X m ) 2 / N
Wo:
- X i - i- ter Wert des Datensatzes
- X m - Mittelwert des Datensatzes
- N - Gesamtzahl der Datenpunkte
Die Formel mag auf den ersten Blick verwirrend aussehen, ist aber wirklich zu bearbeiten. Im Folgenden sind die Schritte aufgeführt, die zur Berechnung der Populationsabweichung ausgeführt werden können:
- Finden Sie heraus, ob es sich bei dem Datensatz, an dem Sie arbeiten, um eine Stichprobe oder eine Grundgesamtheit handelt.
- Finden Sie die Anzahl der Punkte im Datensatz, dh n für die Grundgesamtheit.
- Der nächste Schritt ist das Ermitteln des Mittelwerts. Es ist im Grunde der Durchschnitt aller Werte.
- Ermitteln Sie danach für jeden Datenpunkt die Differenz zwischen dem Mittelwert und dem Quadrat.
- Nehmen Sie die Summe aller Werte im obigen Schritt und dividieren Sie diese durch die Anzahl der in Punkt 2 berechneten Punkte.
Es gibt eine andere Möglichkeit, die Varianz mithilfe der Funktion VAR.P () für die Populationsvarianz und der Funktion VAR.S () für die Stichprobenvarianz in Excel zu berechnen.
Beispiele für Populationsabweichungsformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung der Populationsabweichungsformel besser zu verstehen.
Sie können diese Excel-Vorlage für Populationsabweichungsformeln hier herunterladen - Excel-Vorlage für PopulationsabweichungsformelnPopulationsvarianzformel - Beispiel # 1
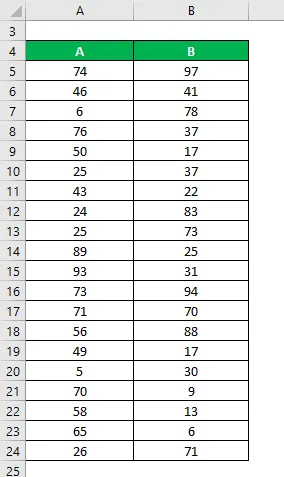
Angenommen, wir haben zwei Beispieldatensätze A und B und jeder enthält 20 zufällige Datenpunkte. Berechnen Sie die Populationsvarianz für beide Datensätze.
Datensatz:
Mittelwert wird berechnet als:
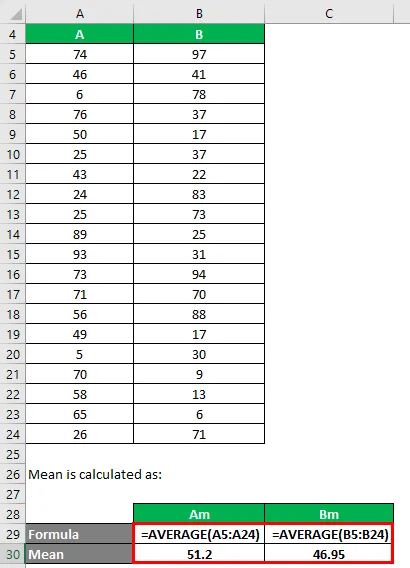
- Mittelwert von Datensatz A = 51, 2
- Mittelwert von Datensatz B = 46, 95
Jetzt müssen wir die Differenz zwischen den Datenpunkten und dem Mittelwert berechnen.
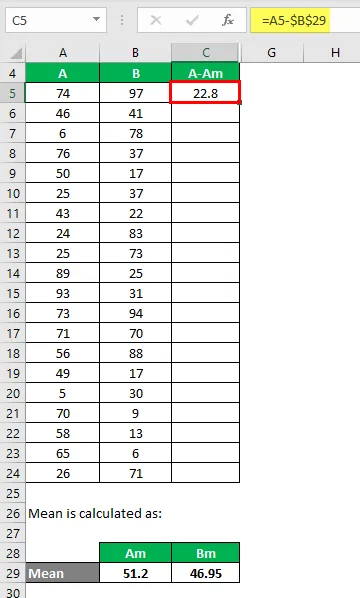
Berechnen Sie auf ähnliche Weise für den gesamten Datensatz von A.
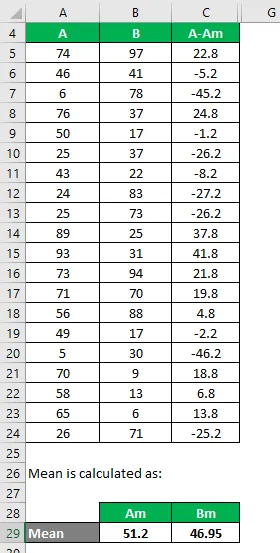
Berechnen Sie es auf ähnliche Weise auch für Datensatz B.
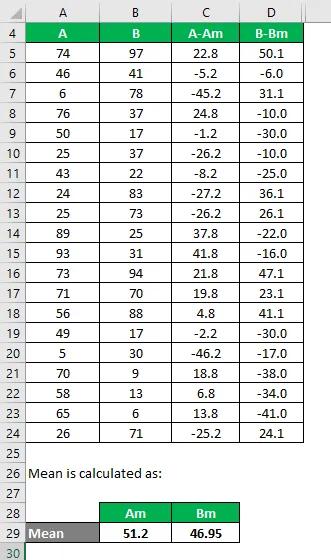
Berechnen Sie das Quadrat der Differenz für beide Datensätze A und B.
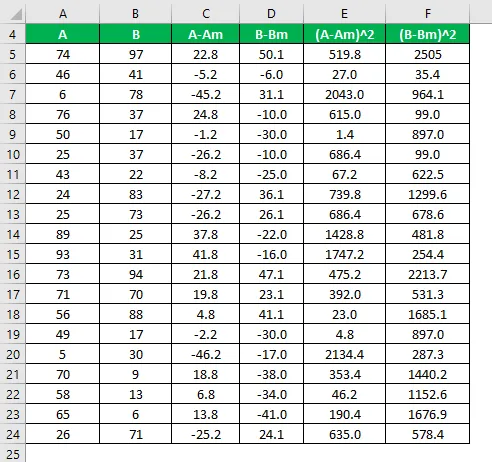
Die Populationsabweichung wird nach der unten angegebenen Formel berechnet
Populationsvarianz = Σ (X i - X m ) 2 / N
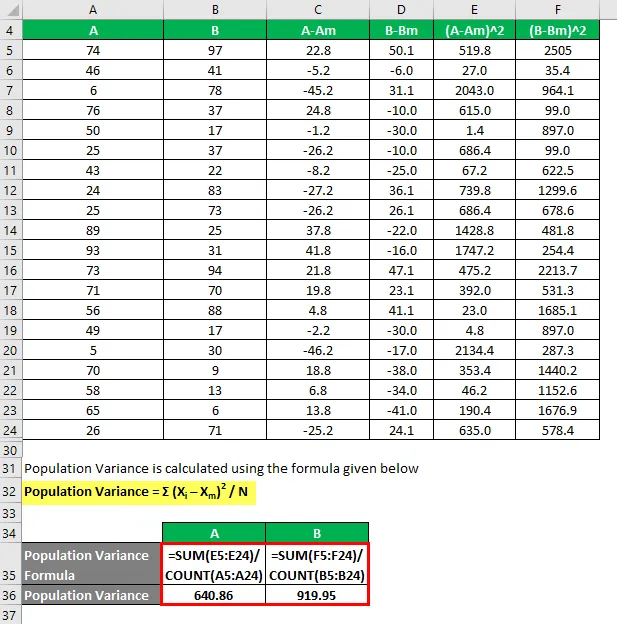
Wenn Sie also hier sehen, hat B mehr Varianz als A, was bedeutet, dass die Datenpunkte von B weiter verteilt sind als A.
Populationsvarianzformel - Beispiel # 2
Angenommen, Sie sind ein risikoaverser Investor und möchten Geld an der Börse anlegen. Da Ihr Risikoappetit gering ist, möchten Sie in sichere Aktien mit geringerer Varianz investieren.
Sie möchten die Bestände auf der Grundlage ihrer früheren Ergebnisse analysieren. Wir haben uns daher entschlossen, eine Stichprobe von 15 Jahren zu ziehen und diese Daten zu verarbeiten. Ihr Finanzberater hat Ihnen 4 Aktien vorgeschlagen, aus denen Sie auswählen können. Sie möchten 2 Aktien aus diesen 4 auswählen und entscheiden dies auf der Grundlage einer geringeren Varianz.
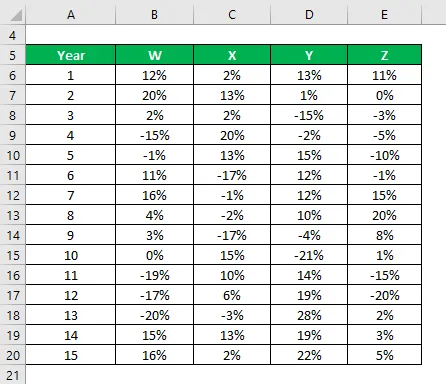
Sie haben Informationen zu den historischen Erträgen der letzten 15 Jahre.
Die Populationsabweichung wird mit der Excel-Formel berechnet
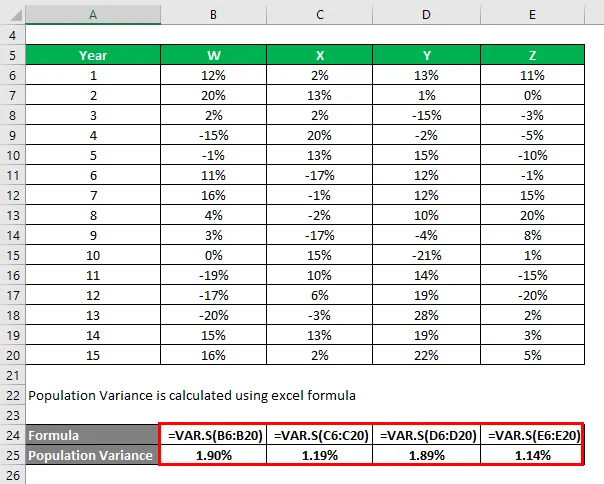
Basierend auf den Informationen wählen Sie Aktien X und Z für die Anlage aus, da diese die geringste Varianz aufweisen.
Erläuterung
Wir diskutieren die Bedeutung von Varianz unter statistischen Gesichtspunkten, sie hilft uns jedoch auch beim Verständnis verschiedener finanzieller Kennzahlen. Varianz ist der Grundstein für die Standardabweichung, die aus der Quadratwurzel der Varianz berechnet wird. Die Standardabweichung ist ein Maß für das Risiko einer Anlage und für das Risiko dieser Anlage. Basierend auf dem Risiko einer Anlage können Anleger dann die Mindestrendite berechnen, die sie zur Kompensation dieses Risikos benötigen. Der Varianzwert ist immer positiv, da er ein Quadrat einer Zahl ist. Dies kann Null sein für einen Datensatz, der alle identischen Elemente enthält.
Relevanz und Verwendung der Populationsvarianzformel
Varianz hilft den Anlegern und Analysten bei der Bestimmung der Standardabweichung, was die Ermittlung des Risiko- und Ertragsverhältnisses oder der Sharpe-Ratio für eine Anlage erleichtert. Grundsätzlich kann jeder eine risikofreie Rendite erzielen, indem er in Schatzanweisungen und risikofreie Wertpapiere investiert. Aber darüber hinaus ist die Überschussrendite und das zu erreichen.
Um die Sharpe Ratio zu erhöhen, ist die Investition besser.
Wie bereits erwähnt, hilft die Varianz beim Auffinden der Standardabweichung, die das Risiko misst. Ein niedrigerer Standardabweichungswert wird jedoch nicht immer bevorzugt. Wenn ein Anleger einen höheren Risikoappetit hat und aggressiver investieren möchte, ist er bereit, ein höheres Risiko einzugehen und eine relativ höhere Standardabweichung als ein risikoaverser Anleger zu bevorzugen. Es kommt also darauf an, welches Risiko ein Anleger eingeht.
Empfohlene Artikel
Dies war ein Leitfaden für die Populationsabweichungsformel. Hier besprechen wir die Berechnung der Populationsabweichung anhand praktischer Beispiele und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Leitfaden zur T-Verteilungsformel
- Beispiele für die relative Standardabweichungsformel
- Wie berechnet man die Kaufkraftparität?
- Formel für die Portfolio-Varianz