
Einführung in komplexe Zahlen in MATLAB
Komplexe Zahlen sind die Kombination von reellen und imaginären Zahlen in Form von p + qi, wobei p und q die reellen Zahlen und i die imaginäre Zahl sind. Eine imaginäre Zahl ist definiert, wobei i das Ergebnis einer Gleichung a 2 = -1 ist. Wir können i oder j verwenden, um die imaginären Einheiten zu bezeichnen. Da in mathematischen Berechnungen komplexe Zahlen verwendet werden, wird Matlab hauptsächlich für mathematische Berechnungen verwendet. Komplexe Zahlen sind daher ein wichtiger Bestandteil des Lernens von Matlab.
Generierung komplexer Zahlen in MATLAB
Komplexe Zahlen können in Matlab mit einer komplexen Funktion erstellt oder deklariert werden. Wir können auch komplexe Zahlen erstellen, indem wir die Quadratwurzel einer beliebigen negativen Zahl ermitteln. In Matlab können wir mit i oder j den Imaginärteil der komplexen Zahl bezeichnen.
Beispiele
X = 4 + 5i
Hier ist X eine komplexe Zahl, die 2 Teile enthält, dh Real- und Imaginärteil. 4 ist der Realteil und 5 ist der Imaginärteil. Wir können die Real- und Imaginärteile mithilfe von Funktionen in Matlab finden.
- a = real (X) = 4 (Dies gibt den Realteil der komplexen Zahl)
- b = imag (X) = 5 (Dies gibt den Imaginärteil der komplexen Zahl)
- complex (6, 7) = 6 + 7i (Mit dieser Funktion wird eine komplexe Zahl erzeugt.)
Wir können auch komplexe Arrays in Matlab erstellen, die auch mit den komplexen Funktionen deklariert werden können.
- a = komplex (x, y)
Es gibt bestimmte Bedingungen für x und y, denen wir folgen sollten, wie x und y nicht einfach oder doppelt sein sollten. Ein komplexer Skalar kann erstellt werden, wenn zwei Eingaben skalarer Natur sind, z.
- X = komplex (5, 3)
- X = 5.0000 + 3.0000i
Ebenso kann ein komplexer Vektor erzeugt werden, wenn wir zwei Eingaben als Vektoren haben.
- X = uint8 ((4; 5; 6; 7));
- Y = uint8 ((3; 5; 1; 2));
- a = komplex (X, Y)
4 + 3i
5 + 5i
6 + 1i
7 + 2i
Wir können eine komplexe Zahl mit nur einem Skalar erstellen,
- X = komplex (10)
- X = 10.0000 + 0.0000i
Es gibt bestimmte Bedingungen, denen die Eingabe- und Ausgabeargumente folgen sollten:
Die Eingabeargumente enthalten Real- und Imaginärteile wie x any y. x und y sollten in MATLAB skalar, vektoriell, mehrdimensional oder matrixförmig sein. x- und y-Größe sollten gleich sein. Sie sollten vom gleichen Datentyp sein, aber es gibt nur wenige Ausnahmen, wie double mit single verwendet werden kann und integer mit double kombiniert werden kann, das skalar ist.
Die Ausgabe des Arrays kann je nach den Eingabeargumenten vektoriell, skalar, matrixförmig oder mehrdimensional sein. Die Größe der Ausgabe sollte mit der der Eingabe übereinstimmen. Wenn die Eingabeargumente andere Datentypen haben als die Ausgabe, wird bestimmt durch:
- Wenn eines der Eingabeargumente von Natur aus einzeln ist, sollte auch die Ausgabe einzeln sein.
- Wenn eines der Eingabeargumente von Natur aus eine Ganzzahl ist, sollte die Ausgabe einen ganzzahligen Datentyp haben.
Mit der Funktion isreal können wir prüfen, ob die Matrix real oder imaginär ist.
Code:
X = (2+i, 1);
Isreal(X)
Ausgabe:

Code:
Isreal (X (2))
Ausgabe:
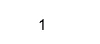
Um die Real- und Imaginärteile zu extrahieren, können wir Real- und Imaginärfunktionen in Matlab wie folgt verwenden:
Code:
real(X)
Ausgabe:
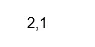
Code:
imag(X)
Ausgabe:

Operationen und Funktionen von komplexen Zahlen in MATLAB
Es gibt verschiedene Operationen und Funktionen, die mit komplexen Zahlen in Matlab ausgeführt werden können
- abs: Mit dieser Funktion wird der Modul einer beliebigen komplexen Zahl in Form von p + qi ermittelt. abs (2 + 3i) = Quadratwurzel von (2 2 + 3 2) = (13) 0, 5
- angle: Ermittelt den Phasenwinkel der komplexen Zahl.
Es gibt bestimmte Tipps, die für das reibungslose Funktionieren komplexer Zahlen in Matlab befolgt werden sollten:
- Wir sollten vermeiden, i und j als Teil von Variablennamen zu verwenden, da sie die Imaginärteile der komplexen Zahl bezeichnen.
- Wir sollten j oder i vermeiden, wenn der Imaginärteil 1 ist. Stattdessen können wir 1j oder 1i verwenden.
- Wir können in Matlab eine komplexe Funktion erstellen, wenn i und j in einem Teil als Variablennamen verwendet werden, die Eingabeargumente nicht vom einfachen oder doppelten Typ sind und der Imaginärteil Null ist.
Fazit
Komplexe Zahlen werden im mathematischen oder technischen Bereich verwendet. Viele reale oder praktische Anwendungen können mit dem Imaginärteil komplexer Zahlen beschrieben werden. Daher ist es wichtig, die Verwendung und Anwendung komplexer Zahlen auf verschiedenen Plattformen zu verstehen, insbesondere wenn Sie sich mit einer physikalischen oder mathematischen Domäne befassen.
Empfohlene Artikel
Dies ist eine Anleitung zu komplexen Zahlen in MATLAB. Hier diskutieren wir die Einführung und Generierung komplexer Zahlen in matlab einschließlich ihrer Beispiele mit Operation und Funktion. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren.
- Wie schreibe ich Funktionen in R?
- Erstellung einer 3D-Matrix in MATLAB
- Top 4 MATLAB-Funktionen
- Funktionen und Vorteile von Versionen in MATLAB