Einführung in Vektoren in Matlab
Ein Vektor ist eine eingeschlossene Menge von Elementen. In Matlab können Vektoren mit eckigen Klammern erstellt werden. Vektoren sind eine der Darstellungen von Arrays (eindimensionales Array). Es kann auf zwei Arten dargestellt werden: Zeilenvektor und Spaltenvektor.
Zeilenvektor
Es ist eine horizontale Menge von Elementen. Es wird in eckigen Klammern dargestellt. Jedes Element ist durch Komma oder Leerzeichen getrennt.
X = (4 7 8) oder X = (4, 7, 8)
Spaltenvektor
Es ist eine vertikale Menge von Elementen. Es wird auch in eckigen Klammern dargestellt. Sie können Spaltenvektoren auf zwei Arten erstellen, indem Sie zuerst jedes Element durch ein Semikolon trennen und auf eine andere Weise jedes Element in die nächste Zeile im Befehlsfenster schreiben.
X = (4; 6; 7) oder
X = (4
6
7)
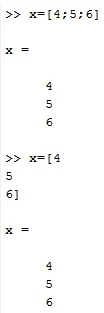
Vektoroperationen
Vektoroperatoren werden grob in zwei Kategorien eingeteilt.
1. Arithmetische Operation
Betrachten wir zwei Vektoren x und y mit den Werten x = (1 4 5 3) und y = (5 3 2 1), so können wir mit diesen beiden Vektoren x und y verschiedene Operationen ausführen.
ein. Multiplikation: Mit dieser Funktion wird mit einem beliebigen arithmetischen Wert der gesamte Vektor multipliziert.
Beispielsweise:
mul = 3 * x
mul = 3 * (1 4 5 3)
mul = (3 12 15 9)
Syntax: variable name = arithmetic constant * vector name

b. Trigonometrische Funktion: Wir können jede trigonometrische Funktion auf vektorähnliche Sünde, cos, tan, cosec, sec usw. anwenden.
Beispiel tri = cos (x)
Die Antwort lautet: 0, 54 - 0, 65 0, 28 - 0, 99
Syntax: variable name = trigonometric function name ( vector name )

Summe: Dies zeigt insgesamt (Addition von) ganzen Elementen in einem Vektor.
Beispiel
x = (1 4 5 3)
Summe = Summe (x)
Die Ausgabe ist total = 13
Syntax: variable name = = sum ( vector name )

c. Länge: Zeigt die Länge eines bestimmten Vektors an, lassen Sie uns einen Vektor p = (9 7 5 3 1 9 7 5 3 1)
Beispiel
p = (9 7 5 3 1 9 7 5 3 1)
Len = Länge (p)
Die Ausgabe ist Len = 10

d. Hinzufügen von Vektoren: Das Hinzufügen von zwei oder mehreren Vektoren ist in Matlab eine einfache Operation. Betrachten wir zwei Vektoren p und q.
P = (4 6 3 2) und q = (5 7 9 1)
Addiere = p + q
Ausgabe ist Add = (9 13 12 3)
Syntax: vector name operator ( + ) vector name

In ähnlicher Weise können wir eine Subtraktionsoperation wie sub = p - q ausführen
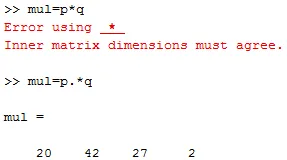
e. Multiplikation von Vektoren: Wenn wir zwei Vektoren multiplizieren möchten, funktioniert ein einfacher Multiplikationsoperator (*) nicht. Deshalb müssen wir einen Punktoperator ('.') Mit einem Multiplikationsoperator hinzufügen.
Beispiel:
P = (4 6 3 2) und q = (5 7 9 1)
mul = p. * q
Ausgabe ist mul = (20 42 27 2)
Syntax: variable name = vector name dot operator multiplication operator vector name
Angenommen, ich möchte das Quadrat eines bestimmten Vektors ermitteln oder den Vektor nur mit diesem Vektor multiplizieren.
Dann lautet die Syntax squr = x. 2
2. Relationale Operation
ein. Gleichbedeutend mit dem Operator : Dieser Operator vergleicht jedes n Element aus zwei Vektoren und gibt eine Ausgabe in der Form Null und Eins aus.
Beispiel
m = (2 5 8)
Und n = (5 5 3)
Wie wir wissen, gibt es drei Elemente in Vektor m und Vektor n,
m == n
Die obige Anweisung gibt die Ausgabe als 0 1 0 aus, was bedeutet, dass das erste Nein nicht gleich ist, die zweite Zahl gleich ist und das dritte Nein nicht gleich ist. O steht für falsch und 1 steht für wahr.

b. Kleiner als Operator (<): Kleiner als der Operator repräsentiert durch das Symbol '<'. Wir können eine gegebene Matrix mit jeder arithmetischen Konstante oder mit jedem anderen Vektor vergleichen.
Beispiel
m = (3 2 4)
n = (1 1 1)
m <n
Die Ausgabe ist 0 0 0, dh alle Zahlen sind größer als der Vektor n.
und wenn m <10
dann ist die Ausgabe 1 1 1, dh alle Zahlen sind kleiner als 10.
c. Größer als Operator (>): Größer als der Operator, der durch das Symbol ('>') dargestellt wird. Wir können eine gegebene Matrix mit jeder arithmetischen Konstante oder mit jedem anderen Vektor vergleichen.
Beispiel:
M = (3 2 4)
N = (1 1 1)
m> n
Die Ausgabe ist 1 1 1, dh alle Werte sind größer als die Werte des Vektors n.
Schlussfolgerung - Vektoren in Matlab
In Matlab können wir verschiedene Vektortypen erstellen, in denen wir verschiedene Operationen wie Addition, Subtraktion, Multiplikation, Quadratwurzel, Potenz, Skalierung, Vektormultiplikation, Punktprodukt usw. ausführen können.
Empfohlene Artikel
Dies ist eine Anleitung zu Vektoren in Matlab. Hier diskutieren wir die Arten von Vektoroperationen, einschließlich arithmetischer und relationaler Operationen, zusammen mit einigen Beispielen. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Datentypen in MATLAB
- Gebrauch Matlab
- Alternativen zu Matlab
- While-Schleife in Matlab
- MATLAB-Funktionen
- Matlab Compiler | Anwendungen von Matlab Compiler