Einführung in das hierarchische Clustering
- Kürzlich hat einer unserer Kunden unser Team gebeten, eine Liste von Segmenten mit einer bestimmten Bedeutung für ihre Kunden zu erstellen, um sie für die Franchise eines ihrer neu eingeführten Produkte zu gewinnen. Nur eine Segmentierung der Kunden mithilfe von partiellem Clustering (k-means, c-fuzzy) wird die Reihenfolge der Wichtigkeit, in der hierarchisches Clustering zum Tragen kommt, nicht deutlich machen.
- Beim hierarchischen Clustering werden die Daten auf der Grundlage einiger Ähnlichkeitsmaße, die als Cluster bezeichnet werden, in verschiedene Gruppen unterteilt, die im Wesentlichen darauf abzielen, die Hierarchie zwischen den Clustern aufzubauen. Es ist im Grunde unbeaufsichtigtes Lernen und die Auswahl der Attribute zur Messung der Ähnlichkeit ist anwendungsspezifisch.
Der Cluster der Datenhierarchie
- Agglomeratives Clustering
- Divisives Clustering
Nehmen wir ein Beispiel von Daten, Noten, die von 5 Schülern erhalten wurden, um sie für einen bevorstehenden Wettbewerb zu gruppieren.
| Schüler | Marks |
| EIN | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Agglomeratives Clustering
- Zunächst betrachten wir jeden einzelnen Punkt / jedes einzelne Element als Cluster und fassen die ähnlichen Punkte / Elemente weiter zusammen, um auf der neuen Ebene einen neuen Cluster zu bilden, bis der einzelne Cluster übrig bleibt. Dies ist ein Bottom-up-Ansatz.
- Einzelbindung und vollständige Bindung sind zwei beliebte Beispiele für agglomeratives Clustering. Andere als die durchschnittliche Verknüpfung und die Schwerpunktverknüpfung. In einer Einzelverknüpfung verbinden wir in jedem Schritt die beiden Cluster, deren zwei engste Mitglieder den geringsten Abstand haben. In vollständiger Verknüpfung verschmelzen wir die Elemente der kleinsten Distanz, die die kleinste maximale paarweise Distanz ergeben.
- Näherungsmatrix. Sie ist der Kern für die Durchführung von hierarchischen Clustern, die den Abstand zwischen den einzelnen Punkten angeben.
- Machen wir eine Näherungsmatrix für unsere in der Tabelle angegebenen Daten, da wir den Abstand zwischen jedem der Punkte mit anderen Punkten berechnen, handelt es sich um eine asymmetrische Matrix der Form n × n, in unserem Fall um 5 × 5-Matrizen.
Eine beliebte Methode zur Entfernungsberechnung sind:
- Euklidische Entfernung (Quadrat)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattan Entfernung
dist((x, y), (a, b)) =|x−c|+|y−d|
Am häufigsten wird der euklidische Abstand verwendet, hier wird derselbe verwendet, und es wird eine komplexe Verknüpfung verwendet.
| Student (Cluster) | EIN | B | C | D | E |
| EIN | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonale Elemente der Näherungsmatrix sind immer 0, da der Abstand zwischen dem Punkt mit demselben Punkt immer 0 ist. Diagonale Elemente sind daher von der Berücksichtigung für die Gruppierung ausgenommen.
In Iteration 1 ist der kleinste Abstand 3, daher verschmelzen wir A und B zu einem Cluster und bilden erneut eine neue Proximity-Matrix mit Cluster (A, B), indem wir (A, B) Clusterpunkt als 10 nehmen, dh Maximum von ( 7, 10) wäre also neu gebildete Proximity-Matrix
| Cluster | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
In Iteration 2 ist 7 der Mindestabstand, daher verbinden wir C und E zu einem neuen Cluster (C, E). Wir wiederholen den in Iteration 1 verfolgten Vorgang, bis wir den einzelnen Cluster erreichen. Hier stoppen wir bei Iteration 4.
Der gesamte Prozess ist in der folgenden Abbildung dargestellt:
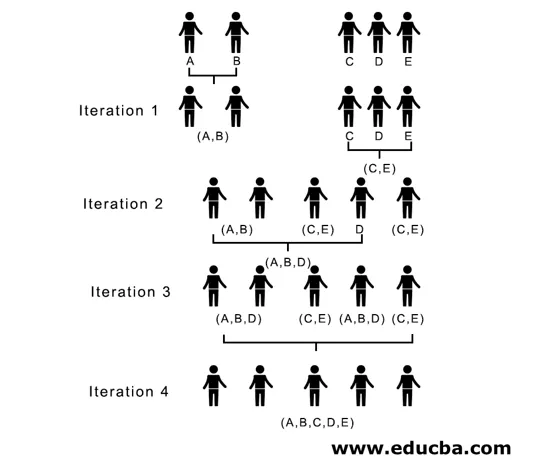
(A, B, D) und (D, E) sind die 2 Cluster, die bei Iteration 3 gebildet wurden. Bei der letzten Iteration, die wir sehen können, verbleibt ein einzelner Cluster.
2. Divisives Clustering
Zunächst betrachten wir alle Punkte als einen einzelnen Cluster und trennen sie durch den größten Abstand, bis wir mit einzelnen Punkten als einzelnen Clustern enden (nicht notwendigerweise können wir in der Mitte anhalten, abhängig von der minimalen Anzahl von Elementen, die wir in jedem Cluster wollen). bei jedem Schritt. Es ist genau das Gegenteil von agglomerativem Clustering und ein Top-Down-Ansatz. Divisives Clustering ist ein Weg, auf dem sich wiederholendes k Clustering bedeutet.
Die Wahl zwischen agglomerativem und divisivem Clustering ist wiederum anwendungsabhängig. Einige Punkte, die berücksichtigt werden müssen, sind:
- Divisiv ist komplexer als agglomeratives Clustering.
- Divisives Clustering ist effizienter, wenn keine vollständige Hierarchie bis hinunter zu einzelnen Datenpunkten erstellt wird.
- Agglomeratives Clustering trifft eine Entscheidung unter Berücksichtigung der lokalen Muster, ohne dass anfänglich globale Muster berücksichtigt werden, die nicht rückgängig gemacht werden können.
Visualisierung der hierarchischen Clusterung
Eine sehr hilfreiche Methode zur Visualisierung von hierarchischen Clustern, die im Geschäftsleben hilfreich ist, ist Dendogram. Dendogramme sind baumartige Strukturen, die die Abfolge von Zusammenführungen und Teilungen aufzeichnen, wobei die vertikale Linie den Abstand zwischen den Clustern darstellt, der Abstand zwischen vertikalen Linien und dem Abstand zwischen den Clustern direkt proportional ist, dh je größer der Abstand ist, desto unterschiedlicher sind die Cluster.
Wir können das Dendogramm verwenden, um die Anzahl der Cluster zu bestimmen. Zeichnen Sie einfach eine Linie, die sich mit einer längsten vertikalen Linie im Dendogramm schneidet. Die Anzahl der geschnittenen vertikalen Linien ist die Anzahl der zu berücksichtigenden Cluster.
Unten sehen Sie das Beispiel-Dendogramm.
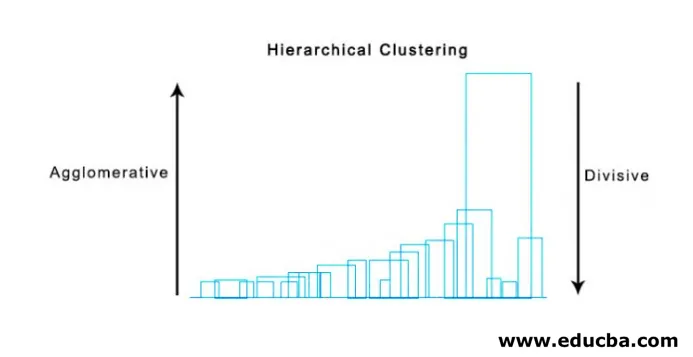
Es gibt ziemlich einfache und direkte Python-Pakete und Funktionen zum Durchführen von hierarchischen Clustern und Zeichnen von Dendogrammen.
- Die Hierarchie von scipy.
- Cluster.hierarchy.dendogram zur Visualisierung.
Allgemeine Szenarien, in denen hierarchisches Clustering verwendet wird
- Kundensegmentierung in Produkt- oder Dienstleistungsmarketing.
- Stadtplanung, um die Orte zu identifizieren, an denen Bauwerke / Dienstleistungen / Gebäude errichtet werden sollen.
- Analyse sozialer Netzwerke: Identifizieren Sie beispielsweise alle MS Dhoni-Fans, um für sein Biopic zu werben.
Vorteile des hierarchischen Clusters
Die Vorteile sind nachfolgend aufgeführt:
- Im Fall von partiellem Clustering wie k-means sollte die Anzahl der Cluster vor dem Clustering bekannt sein, was in praktischen Anwendungen nicht möglich ist, wohingegen beim hierarchischen Clustering keine Vorkenntnisse über die Anzahl der Cluster erforderlich sind.
- Hierarchisches Clustering gibt eine Hierarchie aus, dh eine Struktur, die informativer ist als die unstrukturierte Menge der durch teilweises Clustering zurückgegebenen flachen Cluster.
- Hierarchisches Clustering ist einfach zu implementieren.
- Führt in den meisten Szenarien zu Ergebnissen.
Fazit
Die Art der Clusterbildung macht den großen Unterschied bei der Präsentation von Daten. Hierarchische Clusterbildung ist informativer und einfacher zu analysieren als partielle Clusterbildung. Und es ist oft mit Heatmaps verbunden. Nicht zu vergessen, dass Attribute, die ausgewählt wurden, um Ähnlichkeit oder Unähnlichkeit zu berechnen, vorwiegend sowohl Cluster als auch Hierarchie beeinflussen.
Empfohlene Artikel
Dies ist eine Anleitung zum hierarchischen Clustering. Hier diskutieren wir die Einführung, die Vorteile von Hierarchical Clustering und die allgemeinen Szenarien, in denen Hierarchical Clustering verwendet wird. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren.
- Clustering-Algorithmus
- Clustering im maschinellen Lernen
- Hierarchisches Clustering in R
- Clustering-Methoden
- So entfernen Sie Hierarchie in Tableau?