Einführung in den hierarchischen Clustering-Algorithmus
Der hierarchische Clustering-Algorithmus ist eine unbeaufsichtigte Technik des maschinellen Lernens. Es zielt darauf ab, eine natürliche Gruppierung basierend auf den Merkmalen der Daten zu finden.
Der hierarchische Clustering-Algorithmus zielt darauf ab, verschachtelte Gruppen der Daten durch Aufbau der Hierarchie zu finden. Es ähnelt der biologischen Taxonomie des Pflanzen- oder Tierreichs. Hierarchische Cluster werden im Allgemeinen unter Verwendung des hierarchischen Baums dargestellt, der als Dendrogramm bekannt ist.
Arten des hierarchischen Clustering-Algorithmus
Hierarchische Clustering-Algorithmen gibt es in zwei Typen:
- Teilend
- Agglomerativ
1. Teilend
Dies ist ein Top-Down-Ansatz, bei dem zunächst die gesamten Daten als eine Gruppe betrachtet und dann iterativ in Untergruppen aufgeteilt werden. Wenn die Nummer eines hierarchischen Cluster-Algorithmus bekannt ist, stoppt der Teilungsprozess, sobald die Anzahl der Cluster erreicht ist. Ansonsten stoppt der Prozess, wenn die Daten nicht mehr aufgeteilt werden können. Dies bedeutet, dass die aus der aktuellen Iteration erhaltene Untergruppe mit der aus der vorherigen Iteration übereinstimmt (man kann auch berücksichtigen, dass die Unterteilung stoppt, wenn jeder Datenpunkt ein Cluster ist ).
2. Agglomerativ
Es ist ein Bottom-up-Ansatz, der auf der Verschmelzung von Clustern beruht. Anfangs werden die Daten in m Singleton-Cluster aufgeteilt (wobei der Wert von m die Anzahl der Abtastwerte / Datenpunkte ist). Zwei Cluster werden iterativ zu einem verschmolzen, wodurch die Anzahl der Cluster in jeder Iteration verringert wird. Dieser Vorgang des Zusammenführens von Clustern wird beendet, wenn alle Cluster zu einem Cluster zusammengeführt wurden oder die gewünschte Anzahl von Clustern erreicht ist.
Auf Ebene 1 gibt es m Cluster, die auf Ebene m auf 1 Cluster reduziert werden. Die Datenpunkte, die auf einer niedrigeren Ebene zu einem Cluster zusammengeführt werden, verbleiben auch auf den höheren Ebenen im selben Cluster. Angenommen, es gibt 8 Punkte x1 … x8, also gibt es zunächst 8 Cluster auf Ebene 1. Angenommen, die Punkte x1 und x2 werden auf Ebene 2 zu einem Cluster zusammengeführt, und sie bleiben bis zur Ebene 8 im selben Cluster.
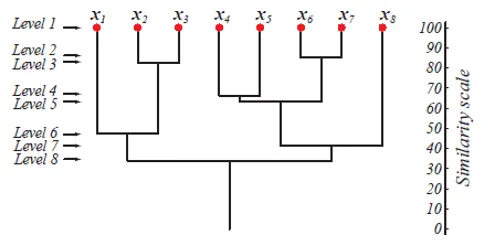
Die obige Abbildung zeigt eine Dendrogrammdarstellung des Agglomerationsclustering-Ansatzes für 8 Datenpunkte sowie die Ähnlichkeitsskala für jede Ebene.
Die Clusterebenen geben uns eine Vorstellung davon, wie ähnlich die Datenpunkte in den Clustern sind. Wie in Abb. 1 gezeigt, werden die Datenpunkte früher zu einem Cluster zusammengeführt, so ähnlich sie auch sind. Daher sind die Datenpunkte in einem Cluster auf Ebene 2 (z. B. x2 und x3) ähnlicher als die Datenpunkte in einem Cluster auf Ebene 6 (z. B. x1 und x2).
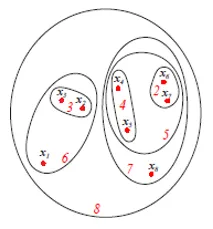
Die obige Abbildung zeigt die Set- oder Venn-Diagrammdarstellung des agglomerativen Clustering-Ansatzes der oben genannten 8 Datenpunkte. Für die Clusterbildung können sowohl Dendrogramme als auch Mengenrepräsentationen verwendet werden. Ein Dendrogramm ist jedoch in der Regel vorzuziehen. Die Darstellung von Assets kann die Clusterähnlichkeiten jedoch nicht quantitativ darstellen.
Schritte für den hierarchischen Clustering-Algorithmus
Befolgen Sie die folgenden Schritte für den hierarchischen Clustering-Algorithmus:
1. Algorithmus
Agglomerativer hierarchischer Clustering-Algorithmus
- Beginnen Sie mit der Initialisierung von c, c1 = n, Di = (xi), i = 1, …, n '
- Mach c1 = c1 - 1
- Finde die nächsten Cluster, sagen wir Di und Dj
- Füge Di und Dj zusammen
- Bis c = c1
- C-Cluster zurückgeben
- Ende
Dieser Algorithmus beginnt mit n Clustern, wobei jeder Datenpunkt ein Cluster ist. Mit jeder Iteration verringert sich die Anzahl der Cluster um 1, wenn die 2 nächsten Cluster zusammengeführt werden. Dieser Vorgang wird fortgesetzt, bis sich die Anzahl der Cluster auf den vordefinierten Wert verringert. C.
Wie kann man entscheiden, welche Cluster sich in der Nähe befinden?
Dies wird unter Verwendung mehrerer Entfernungsmetriken definiert, die wie folgt lauten:
- Der Mindestabstand zwischen den Clustern dmin (Di, Dj). Nützlich für Single.
- Der maximale Abstand zwischen den Clustern dmax (Di, Dj). Nützlich für vollständig.
- Die durchschnittliche Entfernung zwischen den Clustern Davg (Di, Dj).
Was ist Single Linkage und Complete Linkage?
- Wenn dmin (di, dj) verwendet wird, um den Abstand zwischen zwei Clustern zu ermitteln, und der Algorithmus endet, wenn der Abstand zwischen den nächstgelegenen Clustern einen Schwellenwert überschreitet, wird der Algorithmus als einfacher Verknüpfungsalgorithmus bezeichnet.
- Wenn dmax (Di, Dj) verwendet wird, um den Abstand zwischen zwei Clustern zu ermitteln, und der Algorithmus endet, wenn der Abstand zwischen den nächsten Clustern einen Schwellenwert überschreitet, wird der Algorithmus als vollständiger Verknüpfungsalgorithmus bezeichnet.
- Betrachten wir jeden Datenpunkt als Knoten eines Graphen. Es gibt eine Kante zwischen zwei Datenpunkten, wenn sie demselben Cluster angehören. Wenn zwei nächstgelegene Cluster zusammengeführt werden, wird eine Kante hinzugefügt. Es wird eine einzelne Verknüpfung genannt, da ein eindeutiger Pfad von einem Knoten zum anderen vorhanden ist.
- Der vollständige Verknüpfungsalgorithmus führt zwei Cluster zusammen, indem der Abstand zwischen den beiden am weitesten entfernten Punkten minimiert wird.
- Ein einzelner Verknüpfungsalgorithmus generiert einen Spanning Tree. Dieser Algorithmus ist jedoch anfällig für Rauschen. Ein vollständiger Verknüpfungsalgorithmus generiert ein vollständiges Diagramm.
Was ist die zeitliche Komplexität des Algorithmus?
Angenommen, wir haben n Muster im d-dimensionalen Raum und verwenden dmin (Di, Dj), um c-Cluster zu bilden. Wir müssen n (n - 1) Zwischenpunktabstände berechnen, von denen jeder eine O (d 2 ) -Berechnung ist, und die Ergebnisse in eine Zwischenpunktabstandstabelle einfügen. Die Raumkomplexität ist O (n 2 ). Um das Mindestabstandspaar (für das erste Zusammenführen) zu finden, müssen wir die vollständige Liste durchgehen und den Index des kleinsten Abstands beibehalten.
Somit ist für den ersten Agglomerationsschritt die Komplexität O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Für einen weiteren willkürlichen Agglomerationsschritt (dh von c1 zu c1 - 1) gehen wir lediglich die n (n - 1) - c1 "unbenutzten" Abstände in der Liste durch und finden die kleinsten, für die x und x 'in verschiedenen Clustern liegen . Dies ist wiederum O (n (n - 1) - c1). Die Gesamtzeitkomplexität ist somit O (cn 2 d 2 ) und unter typischen Bedingungen n >> c.
2. Visualisierung
Nachdem die Daten in Cluster aufgeteilt wurden, empfiehlt es sich, die Cluster zu visualisieren, um eine Vorstellung davon zu erhalten, wie die Gruppierung aussieht. Die Visualisierung dieser hochdimensionalen Daten ist jedoch schwierig. Daher verwenden wir zur Visualisierung die Hauptkomponentenanalyse (PCA). Nach der PCA erhalten wir die Datenpunkte im niedrigdimensionalen Raum (im Allgemeinen 2D oder 3D), die wir zeichnen können, um die Gruppierung zu sehen.
Hinweis: Hohe Dimension bedeutet eine große Anzahl von Features und keine Anzahl von Datenpunkten.3. Bewertung
Eine der Methoden zur Bewertung von Clustern besteht darin, dass der Abstand der Punkte zwischen den Clustern (Intercluster-Abstand) viel größer sein sollte als der Abstand der Punkte innerhalb des Clusters (Intracluster-Abstand).
Fazit
Im Folgenden sind die wenigen wichtigen Imbissbuden aufgeführt:
- Der hierarchische Clustering-Algorithmus wird verwendet, um verschachtelte Muster in Daten zu finden
- Hierarchisches Clustering besteht aus zwei Typen - Divisiv und Agglomerativ
- Dendrogramm und Set / Venn-Diagramm können zur Darstellung verwendet werden
- Durch eine einzelne Verknüpfung werden zwei Cluster zusammengeführt, indem der Mindestabstand zwischen ihnen minimiert wird. Es bildet sich eine Spannweite
- Durch die vollständige Verknüpfung werden zwei Cluster zusammengeführt, indem der maximale Abstand zwischen ihnen minimiert wird. Es wird eine vollständige Grafik erstellt.
- Die Gesamtzeitkomplexität des hierarchischen Clustering-Algorithmus beträgt O (cn 2 d 2 ), wobei c die vordefinierte Anzahl von Clustern ist, n die Anzahl von Mustern ist und d der d-dimensionale Raum der n Muster ist.
Empfohlene Artikel
Dies ist eine Anleitung zum hierarchischen Clustering-Algorithmus. Hier diskutieren wir die Typen und Schritte hierarchischer Clustering-Algorithmen. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren.
- Hierarchische Clusteranalyse
- Hierarchisches Clustering in R '
- Clustering-Algorithmus
- Was ist Clustering in Data Mining?
- Hierarchisches Clustering | Agglomeratives & Divisives Clustering
- C ++ Algorithmus | Beispiele für den C ++ - Algorithmus