
Einführung in das hierarchische Clustering in R
Hierarchisches Clustering in R ist die häufigste Form des Lernens. Clustering ist einer der Algorithmen des maschinellen Lernens, der die Schlussfolgerungen aus den unbeschrifteten Daten zieht.
Es gibt hauptsächlich zwei Arten von Algorithmen für maschinelles Lernen:
- Betreute Lernalgorithmen
- Unüberwachte Lernalgorithmen
Überwachte Lernalgorithmen sind eine Kategorie eines maschinellen Lernalgorithmus, bei dem die Maschine aus den gekennzeichneten Daten lernt. Ein Beispiel für überwachte Lernalgorithmen ist die Klassifizierung und Regression. Unüberwachte Lernalgorithmen sind eine Kategorie eines maschinellen Lernalgorithmus, bei dem die Maschine aus den unbeschrifteten Daten lernt. Ein Beispiel für unbeaufsichtigte Lernalgorithmen sind Clustering-Algorithmen.
Wie funktioniert Clustering?
Clustering-Algorithmen gruppieren eine Reihe ähnlicher Datenpunkte in Cluster. Das Hauptziel des Clustering-Algorithmus besteht darin, Cluster von Datenpunkten zu erstellen, die in den Features ähnlich sind. Mit anderen Worten, Datenpunkte in einem Cluster sind ähnlich und Datenpunkte in einem Cluster unterscheiden sich von Datenpunkten in einem anderen Cluster.
Der hierarchische Clustering-Algorithmus verwendet hauptsächlich zwei Ansätze:
1. Agglomerativ
Es beginnt mit jeder Beobachtung in einem einzelnen Cluster und basierend auf dem Ähnlichkeitsmaß in der Beobachtung werden die Cluster weiter zusammengeführt, um einen einzelnen Cluster zu bilden, bis keine weitere Zusammenführung mehr möglich ist. Dieser Ansatz wird als agglomerativer Ansatz bezeichnet.
2. Teilend
Es beginnt mit allen Beobachtungen in einem einzelnen Cluster und weiteren Teilungen basierend auf dem Ähnlichkeitsmaß oder dem Unähnlichkeitsmaß-Cluster, bis keine Teilung mehr möglich ist. Dieser Ansatz wird als Teilungsmethode bezeichnet.
Beginnen wir nun mit hierarchischen Clustering-Algorithmen. Hierarchisches Clustering kann von oben nach unten oder von unten nach oben durchgeführt werden. Wir beginnen mit einem Bottom-up-Ansatz oder einem agglomerativen Ansatz, bei dem wir für jeden Datenpunkt einen Cluster erstellen und dann Cluster basierend auf einem Ähnlichkeitsmaß in den Datenpunkten zusammenführen. Der nächste wichtige Punkt ist, wie wir die Ähnlichkeit messen können. Es gibt viele Entfernungsmatrizen wie Euklidisch, Jaccard, Manhattan, Canberra, Minkowski usw., um das Unähnlichkeitsmaß zu finden. Die Wahl der Distanzmatrix hängt von der Art des verfügbaren Datensatzes ab. Wenn der Datensatz beispielsweise fortlaufende numerische Werte enthält, ist die gute Wahl die euklidische Distanzmatrix, während Jaccard die gute Wahl ist, wenn der Datensatz binäre Daten enthält Entfernungsmatrix und so weiter.
Implementieren von hierarchischem Clustering in R
Die zur Implementierung des hierarchischen Clusters in R erforderlichen Schritte sind:
1. Installieren Sie alle erforderlichen R-Pakete
Wir werden die folgenden Pakete verwenden, installieren Sie also alle diese Pakete, bevor Sie verwenden:
install.packages ( "cluster" ) # for clustering algorithms
install.packages ( "tidyverse" ) # for data manipulation
install.packages ( "factoextra" ) # for clustering visualization
# includes package in R as –
library ( "cluster" )
library( "tidyverse" )
library( "factoextra" )
2. Datenaufbereitung
Die Daten Für die hierarchische Clusteranalyse vorbereiten. Dieser Schritt ist sehr grundlegend und wichtig. Wir müssen hier hauptsächlich zwei Aufgaben ausführen, nämlich Skalieren und Schätzen des fehlenden Werts. Die Daten müssen skaliert oder standardisiert oder normalisiert werden, um Variablen vergleichbar zu machen. Das skalierte oder standardisierte oder normalisierte ist ein Prozess des Transformierens der Variablen, so dass sie eine Standardabweichung von eins und einen Mittelwert von null haben sollten.
Wenn in unserem Datensatz ein fehlender Wert vorhanden ist, ist es sehr wichtig, den fehlenden Wert zu unterstellen oder den Datenpunkt selbst zu entfernen. Es stehen verschiedene Optionen zur Verfügung, um den fehlenden Wert wie Durchschnitts-, Mittel- und Medianwert anzurechnen, um den fehlenden Wert zu schätzen. Zum Beispiel verwenden wir hier einen integrierten Iris-Datensatz, in dem wir den Iris-Pflanzentyp gruppieren möchten. Der Iris-Datensatz enthält 3 Klassen für jede Klasse-50-Instanz. Es enthält 5 Funktionen als Sepal. Länge, Sepal.Width, Petal.Length, Petal.Width und Species.
Der R-Code:
data <- iris
print(data)
# the sample of data set showing below which contain 1 sample for each class
"Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"
1 4, 9 3, 5 1, 3 0, 2 setosa
51 7, 0 3, 1 4, 5 1, 3 Versicolor
101 6, 3 3, 2 6, 0 1, 9 Virginia
data <- na.omit(data) # remove missing value
data <- scale(df) # scaling the variables or features
3. Geben Sie an, welche hierarchischen Clustering-Algorithmen verwendet werden
Die verschiedenen Arten von hierarchischen Clustering-Algorithmen wie agglomeratives hierarchisches Clustering und divisives hierarchisches Clustering stehen in R zur Verfügung. Die erforderlichen Funktionen sind:
- Agglomeratives hierarchisches Clustering (HC): hclust-Funktion, die im Statistikpaket verfügbar ist, und Agnes-Funktion, die im Clusterpaket verfügbar ist) für
- Divisives hierarchisches Clustering: Diana-Funktion, die im Clusterpaket verfügbar ist.
4. Hierarchisches Clustering berechnen
Um das hierarchische Clustering zu berechnen, muss die Distanzmatrix berechnet und der Datenpunkt auf den richtigen Cluster gesetzt werden. Es gibt verschiedene Möglichkeiten, wie wir den Abstand zwischen den Clustern berechnen können:
Vollständige Verknüpfung: Die maximale Entfernung zwischen den Clustern wird vor dem Zusammenführen berechnet.
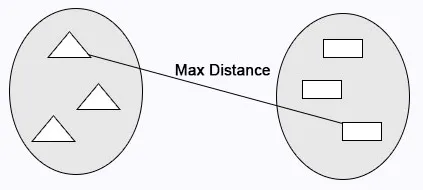
Single Linkage: Der Mindestabstand zwischen den Clustern wird vor dem Zusammenführen berechnet.
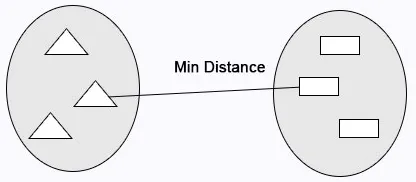
Durchschnittliche Verknüpfung: Berechnet die durchschnittliche Entfernung zwischen Clustern vor dem Zusammenführen.
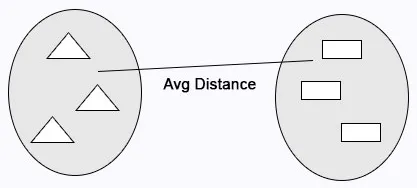
R-Code:
cluster <- hclust(data, method = "average" )
Centroid Linkage: Der Abstand zwischen den beiden Centroiden der Cluster wird vor dem Zusammenführen berechnet.
R-Code:
# matrix of Dissimilarity
dis_mat <- dist(data, method = "euclidean")
# Hierarchical clustering using Complete Linkage
cluster <- hclust(data, method = "complete" )
# or Compute with agnes
cluster <- agnes(data, method = "complete")
5. Dendrogramme
Das Dendrogramm wird verwendet, um die Anzahl der erhaltenen Cluster zu verwalten. Es verhält sich genauso wie in k, dh k steuert die Anzahl der Cluster. Die aktuelle Funktion, mit der wir das Dendrogramm schneiden können.
R-Code:
cutree(as.hclust(cluster), k = 3)
Der vollständige R-Code:
ibrary(scatterplot3d)
data <- iris
print( data )
data <- na.omit(data)
data <- scale(data)
# matrix of Dissimilarity
dis_mat <- dist(data, method = "euclidean")
# creating hierarchical clustering with Complete Linkage
cluster <- hclust(data, method = "complete" )
# Dendrogram plot
plot(cluster)
# or agnes can be used to compute hierarchical clustering
Cluster2 <- agnes(data, method = "complete")
# Dendrogram plot
plot(cluster2)
Die Darstellung des obigen R-Codes:
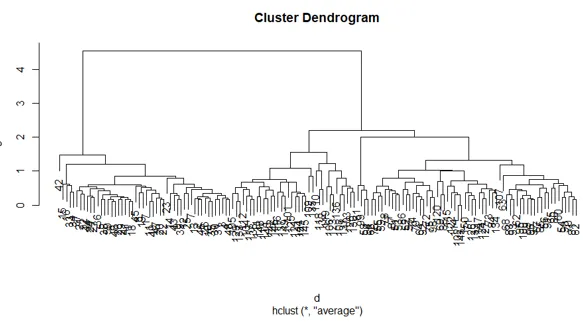
Fazit
Es gibt hauptsächlich zwei Arten von Algorithmen für maschinelles Lernen, überwachtes Lernen und nicht überwachtes Lernen. Clustering-Algorithmen sind ein Beispiel für nicht überwachte Lernalgorithmen. Clustering-Algorithmen gruppieren eine Reihe ähnlicher Datenpunkte in Cluster. Es gibt hauptsächlich zwei Ansätze für den hierarchischen Clustering-Algorithmus, wie unten angegeben: agglomeratives hierarchisches Clustering und divisives hierarchisches Clustering.
Empfohlene Artikel
Dies ist eine Anleitung zum hierarchischen Clustering in R. Hier wird detailliert erläutert, wie das Clustering funktioniert und wie hierarchisches Clustering in R implementiert wird. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren.
- Clustering-Algorithmus
- Was ist Clustering in Data Mining?
- Clustering-Methoden
- Methoden des maschinellen Lernens
- Überblick über die hierarchische Clusteranalyse
- Liste der R-Pakete