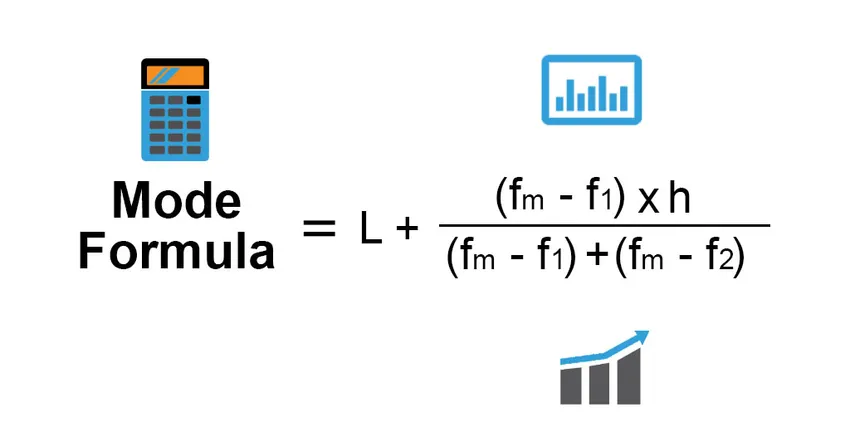
Modus Formel (Inhaltsverzeichnis)
- Formel
- Beispiele
- Taschenrechner
Was ist die Modusformel?
Die drei zentralen Tendenzmaße sind Mean Median und Mode. Wenn alle drei zusammen verwendet werden, um eine aussagekräftige Analyse im Datensatz zu extrahieren. Heute werden wir in diesem Artikel den Modus diskutieren, der auch einer der Schlüssel und die wichtige Methode der zentralen Tendenz ist. Modus bezieht sich auf den am häufigsten vorkommenden Wert im Datensatz. Der Modus eines Datensatzes kann mit normalem Datensatz, Gruppendatensatz sowie nicht gruppiertem oder nicht gruppiertem Datensatz ermittelt werden. Der am häufigsten verwendete Mittelwert bleibt jedoch trotz der Existenz von Mittelwert, Median und Modus das beste Maß für die zentrale Tendenz. In diesem Artikel werden wir versuchen, die Modusfunktion, Beispiele und Erklärungen jedes Beispiels zusammen mit der Formel und den Berechnungen zu verstehen.
Die Formel für den Modus lautet:
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Modusformel für gruppierte Daten:
Modus = L + (fm - f1) h / 2fm - f1 - f2
Wo,
- L = Untergrenze Modus der modalen Klasse
- fm = Häufigkeit der Modalklasse
- f1 = Häufigkeit der Klasse vor der modalen Klasse
- f2 = Häufigkeit der Klasse, die der modalen Klasse folgt
- h = Größe des Klassenintervalls
Beispiele für Modusformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung von Mode besser zu verstehen.
Sie können diese Excel-Vorlage für Modusformeln hier herunterladen - Excel-Vorlage für ModusformelnModusformel - Beispiel # 1
Wo der Modus berechnet wird, ist einfach die Anzahl der Beobachtungen in einem Datensatz, die die meiste Zeit auftreten.
Berechnen Sie den Modus des folgenden Datensatzes.
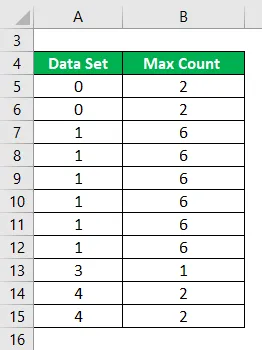
Lösung:
Ein Modus wird berechnet als:
Anzahl der Beobachtungen in einem Datensatz, die die meiste Zeit auftreten
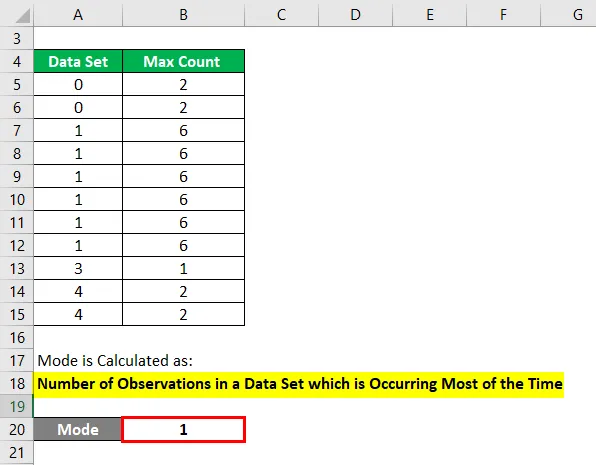
- Modus = 1
Modusformel - Beispiel # 2
Berechnen Sie den Modus anhand der angegebenen Informationen.
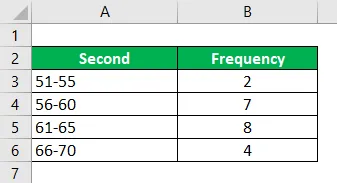
Lösung:
Hinweis: - Zuerst muss die Modalgruppe mit der höchsten Frequenz identifiziert werden. Wenn das Intervall nicht kontinuierlich ist, sollte 0, 5 vom unteren Grenzmodus subtrahiert und 0, 5 vom oberen Grenzmodus addiert werden. Dann wird das Intervall sein
Die modale Gruppe wird berechnet als:
Modale Gruppe, die am häufigsten vorkommt, dh 60, 5-65, 5
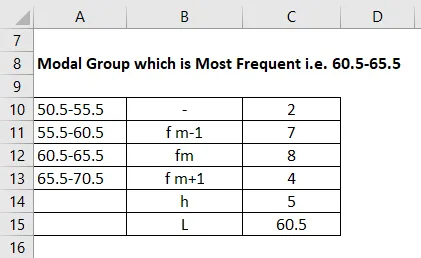
Dann gehört die niedrigere Frequenz zu der modalen Gruppe, die 4 ist. In diesem Fall wird fm + 1 angenommen und fm-1 wird in diesem Beispiel zu 7. Und wir haben fm, das ist die Frequenz als 8. Das (h) heißt Die Größe des Klassenintervalls beträgt 5, wobei wir auch das Startintervall berücksichtigen. L ist 60, 5.
Der Modus wird mit der unten angegebenen Formel berechnet
Modus = L + (fm - f1) h / (fm - f1) + (fm - f2)
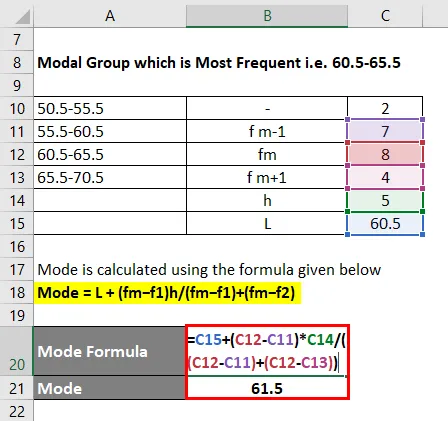
- Modus = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Modus = 61, 5
Modusformel - Beispiel # 3
Das Folgende sind die Höhenverteilungen in einer bestimmten Klasse von Schülern in einem bestimmten Modus
Berechnen Sie den Modus anhand der angegebenen Informationen.
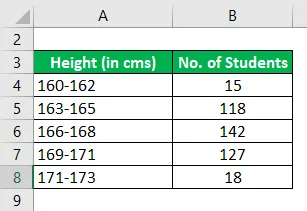
Lösung:
Wenn das Intervall nicht kontinuierlich ist, sollte 0, 5 vom unteren Grenzmodus abgezogen und 0, 5 vom oberen Grenzmodus addiert werden. Dann wird das Intervall sein
Die modale Gruppe wird berechnet als:
Modale Gruppe, die am häufigsten vorkommt, dh 165, 5-168, 5
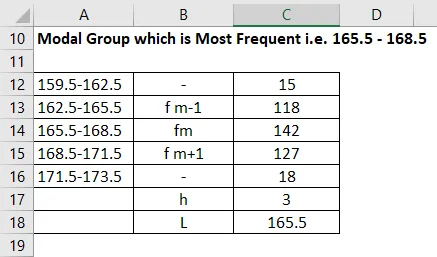
Der Modus wird mit der unten angegebenen Formel berechnet
Modus = L + (fm - f1) h / (fm - f1) + (fm - f2)
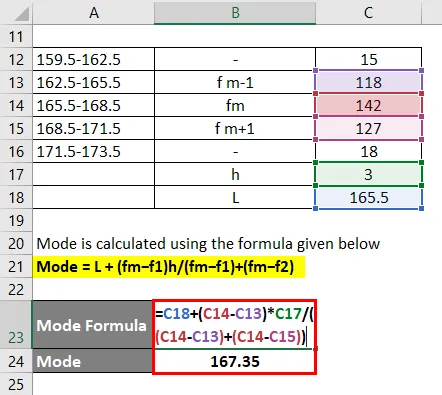
- Modus = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Modus = 167, 35
Erläuterung
Der Modus kann einfach als der Wert erklärt werden, der im Datensatz am häufigsten vorkommt. Und der obige Modus kann so erklärt werden, dass wenn Daten eine Gruppe sind, wir zuerst die Modalfunktion berechnen und die Daten auch stetig machen müssen, um den Modus der Daten zu berechnen. Die modale Klasse wird mit der Klasse bestimmt, die die höchste Häufigkeit im Datensatz hat.
Relevanz und Verwendung der Modusformel
- Mittelwert, Median und Modus decken verschiedene Aspekte Ihrer Daten auf. Jeder wird Ihnen eine allgemeine Vorstellung geben, kann Sie jedoch irreführen. Wenn Sie alle drei haben, erhalten Sie ein vollständigeres Bild
- Für eine Normalverteilung haben der Modus, der Mittelwert und der Median den gleichen Wert, da Modus eine Normalverteilung ist. Der isolierte Analysemodus spiegelt nicht das wahre Bild wider. Wenn Sie den gesamten Datensatz analysieren möchten, sollten alle drei statistischen Kennzahlen detailliert analysiert und interpretiert werden
- Der Modus ist leicht zu verstehen und einfach zu berechnen.
- Der Modus wird nicht von extrem großen oder kleinen Werten beeinflusst.
- Der Modus kann nur durch Inspektion von nicht gruppierten Daten und diskreter Häufigkeitsverteilung lokalisiert werden.
- Der Modus kann für qualitative Daten nützlich sein.
- Der Modus kann in einer endlosen Frequenztabelle berechnet werden.
- Der Modus kann grafisch lokalisiert werden
- Der Modus wird am häufigsten von Datenwissenschaftlern verwendet
- Der Modus ist, dass er uns kein sehr gutes Maß für die zentrale Tendenz liefert, wenn die häufigste Marke weit vom Rest der Daten im Datensatz entfernt ist
Modus Formelrechner
Sie können den folgenden Modusformelrechner verwenden
| L | |
| fm | |
| f1 | |
| f2 | |
| h | |
| Modus Formel | |
| Modus Formel = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Empfohlene Artikel
Dies ist eine Anleitung zur Modusformel. Hier besprechen wir die Berechnung der Modusformel zusammen mit praktischen Beispielen. Wir bieten auch einen Modusrechner mit einer herunterladbaren Excel-Vorlage an. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Beispiele für die Gordon Growth Model Formula
- Formel zur Berechnung des Capital Asset Pricing-Modells
- Rechner für die Formel der Gesamtkostenquote
- Poisson-Verteilungsformel (Beispiele mit Excel-Vorlage)