Regressionsanalyse in Excel - Verwendung der Regressionsanalyse (Beispiel)

• Regressionsanalyse in Excel

Excel-Regressionsanalyse (Inhaltsverzeichnis)

• Regressionsanalyse in Excel
• Erklärung der Regression mathematisch
• Durchführen einer linearen Regression in Excel
  • Nr. 1 - Regressionstool Verwenden von Analysis ToolPak in Excel
  • # 2 - Regressionsanalyse mit Scatterplot mit Trendlinie in Excel

Regressionsanalyse in Excel

Die lineare Regression ist eine statistische Technik, die die lineare Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen untersucht.

• Abhängige Variable (auch als Antwort- / Ergebnisvariable bezeichnet): Ist die Variable, die Sie interessieren und die Sie basierend auf den verfügbaren Informationen der unabhängigen Variablen vorhersagen möchten.
• Unabhängige Variable (auch als Erklärungs- / Prädiktorvariable bezeichnet): Ist / sind die Variable (n), von denen die Antwortvariable abhängt. Das heißt, dies sind die Variablen, mit denen die Antwortvariable vorhergesagt werden kann.

Lineare Beziehung bedeutet, dass die Änderung einer unabhängigen Variablen eine Änderung der abhängigen Variablen verursacht.

Grundsätzlich gibt es auch zwei Arten von linearen Beziehungen.

1. Positive lineare Beziehung: Wenn die unabhängige Variable zunimmt, nimmt auch die abhängige Variable zu.
2. Negative lineare Beziehung: Wenn die unabhängige Variable zunimmt, nimmt die abhängige Variable ab.

Dies waren einige der Voraussetzungen, bevor Sie mit der Regressionsanalyse in Excel fortfahren können.

Es gibt zwei grundlegende Möglichkeiten, eine lineare Regression in Excel durchzuführen:

• Regressionstool über Analysis ToolPak
• Streudiagramm mit Trendlinie

Es gibt tatsächlich eine weitere Methode, die manuelle Formeln zur Berechnung der linearen Regression verwendet. Aber warum sollten Sie es versuchen, wenn Excel Berechnungen für Sie durchführt?

Daher werden wir nur über die beiden oben diskutierten Methoden sprechen.

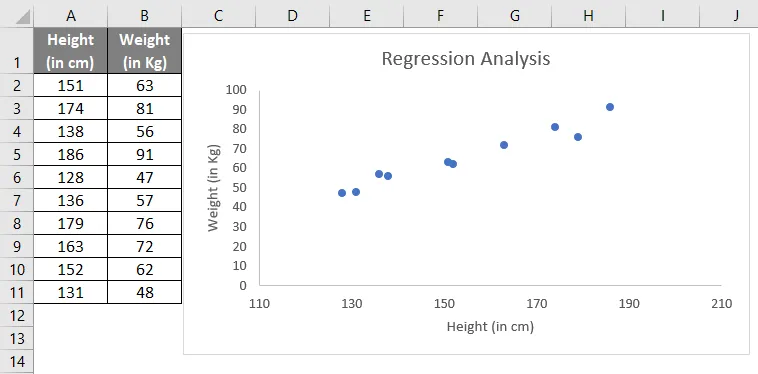
Angenommen, Sie haben Daten zu Größe und Gewicht von 10 Personen. Wenn Sie diese Informationen in einem Diagramm darstellen, sehen wir uns an, was es gibt.

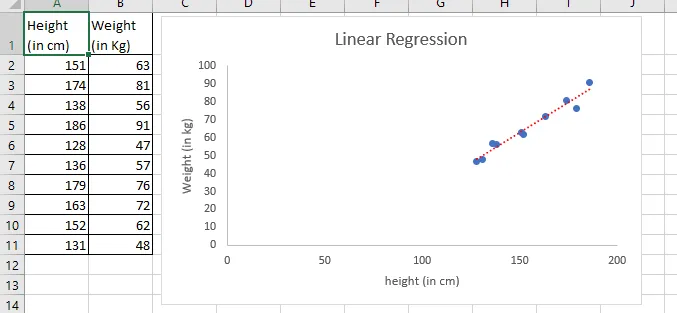
Wie der obige Screenshot zeigt, kann die lineare Beziehung in Höhe und Gewicht über das Diagramm ermittelt werden. Lassen Sie sich jetzt nicht viel auf Graph ein, wir werden es jedenfalls im zweiten Teil dieses Artikels vertiefen.

Erklärung der Regression mathematisch

Wir haben einen mathematischen Ausdruck für die lineare Regression wie folgt:

Y = aX + b + & epsi ;.

Wo,

• Y ist eine abhängige Variable oder Antwortvariable.
• X ist eine unabhängige Variable oder ein Prädiktor.
• a ist die Steigung der Regressionslinie. Dies bedeutet, dass sich Y bei einer Änderung von X um „a“ -Einheiten ändert.
• b fängt ab. Dies ist der Wert, den Y annimmt, wenn der Wert von X Null ist.
• ε ist der Zufallsfehlerterm. Tritt auf, weil der vorhergesagte Wert von Y niemals exakt mit dem tatsächlichen Wert für gegebenes X übereinstimmt. Dieser Fehlerbegriff ist für uns kein Grund zur Sorge. Da es einige Software gibt, die die Berechnung dieses Fehlerbegriffs im Backend für Sie erledigen. Excel ist eine dieser Software.

In diesem Fall lautet die Gleichung:

Y = aX + b

Welche können dargestellt werden als:

Gewicht = a * Höhe + b

Wir werden versuchen, die Werte von a und b mit den oben beschriebenen Methoden herauszufinden.

Durchführen einer linearen Regression in Excel

Der weitere Artikel erklärt die Grundlagen der Regressionsanalyse in Excel und zeigt verschiedene Möglichkeiten zur linearen Regression in Excel.

Sie können diese Excel-Vorlage für die Regressionsanalyse hier herunterladen - Excel-Vorlage für die Regressionsanalyse

Nr. 1 - Regressionstool Verwenden von Analysis ToolPak in Excel

In unserem Beispiel versuchen wir, die Regression für Gewichtswerte (die abhängige Variable) mithilfe von Höhenwerten (die eine unabhängige Variable sind) anzupassen.

• Klicken Sie in der Excel-Tabelle unter Daten auf Datenanalyse (unter Analysegruppe ) .

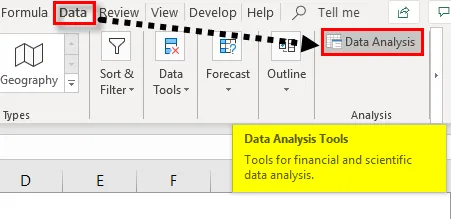
• Suchen Sie nach Regression . Wählen Sie es aus und drücken Sie OK.

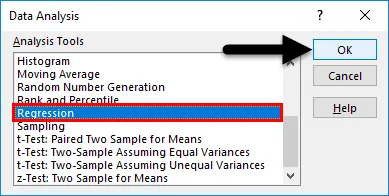
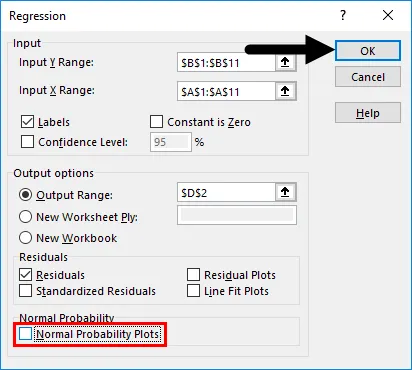
• Verwenden Sie die folgenden Eingaben im sich öffnenden Bereich Regression .

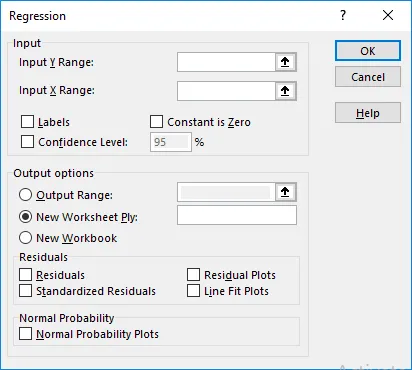
• Y-Bereich eingeben : Wählen Sie die Zellen aus, die Ihre abhängige Variable enthalten (in diesem Beispiel B1: B11).

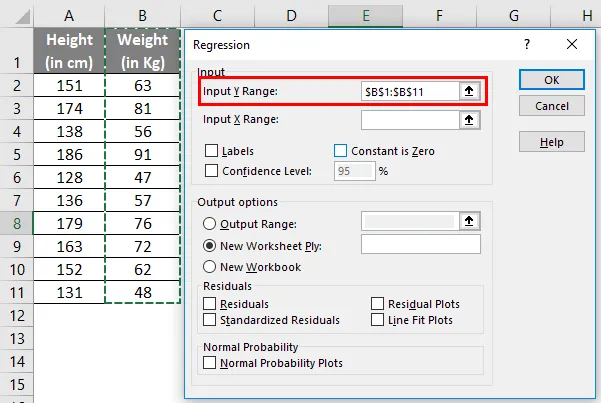
• X-Bereich eingeben : Wählen Sie die Zellen aus, die Ihre unabhängige Variable enthalten (in diesem Beispiel A1: A11).

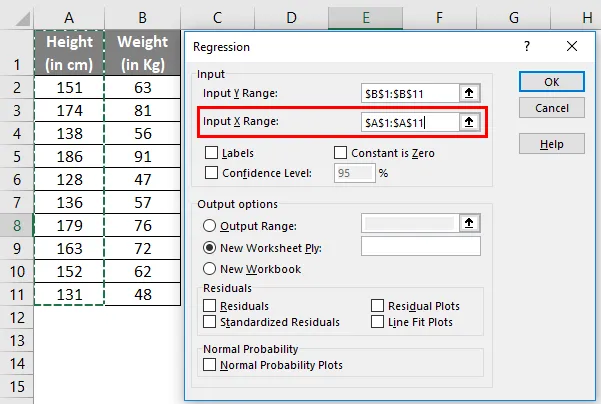
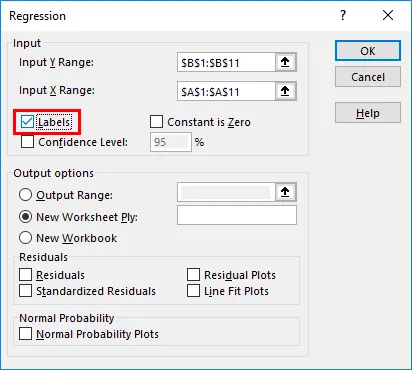
• Aktivieren Sie das Kontrollkästchen Labels, wenn Ihre Daten Spaltennamen haben (in diesem Beispiel haben wir Spaltennamen).

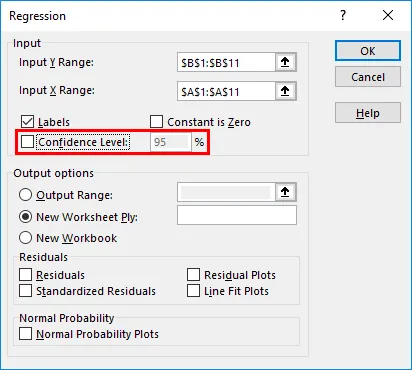
• Das Konfidenzniveau ist standardmäßig auf 95% festgelegt, was gemäß den Benutzeranforderungen geändert werden kann.

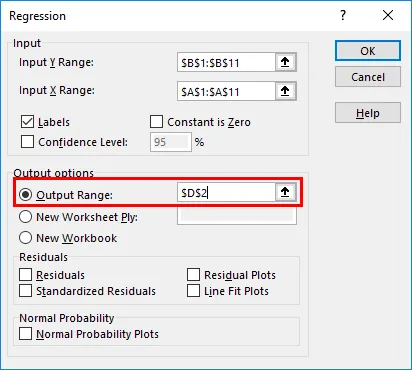
• Unter Ausgabeoptionen können Sie anpassen, wo die Ausgabe der Regressionsanalyse in Excel angezeigt werden soll. In diesem Fall möchten wir die Ausgabe auf demselben Blatt sehen. Daher wird der Bereich entsprechend angegeben.

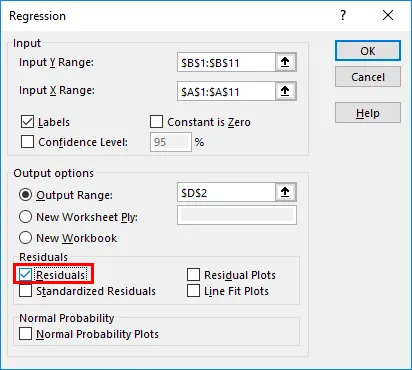
• Unter der Option Residuen haben Sie optionale Eingaben wie Residuen, Residuendiagramme, standardisierte Residuen, Geradenanpassungsdiagramme, die Sie je nach Bedarf auswählen können. Aktivieren Sie in diesem Fall das Kontrollkästchen Residuen, um die Streuung zwischen vorhergesagten und tatsächlichen Werten anzuzeigen.

• Unter der Option Normale Wahrscheinlichkeit können Sie Normale Wahrscheinlichkeitsdiagramme auswählen, mit denen Sie die Normalität von Prädiktoren überprüfen können. Klicken Sie auf OK .

• Excel berechnet die Regressionsanalyse für Sie in Sekundenbruchteilen.

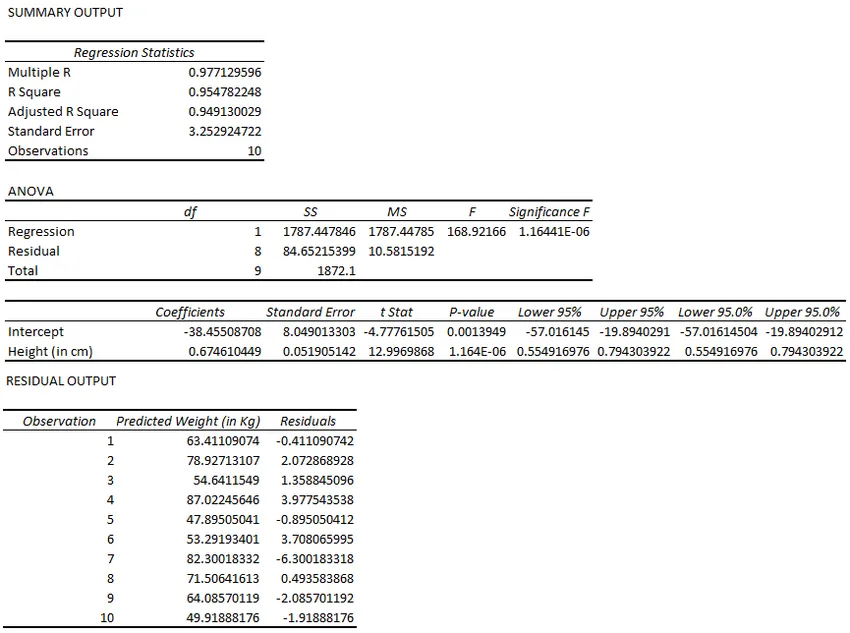
Bis hierher war es einfach und nicht so logisch. Es ist jedoch eine schwierige Aufgabe, diese Ausgabe zu interpretieren und daraus wertvolle Erkenntnisse zu gewinnen.

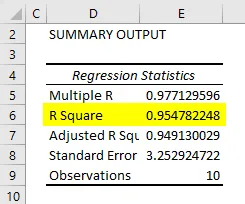
Ein wichtiger Teil dieser gesamten Ausgabe ist R Square / Adjusted R Square in der SUMMARY OUTPUT-Tabelle. Was Auskunft gibt, wie gut unser Modell passt. In diesem Fall beträgt der R Square- Wert 0, 9547. Was bedeutet, dass das Modell eine Genauigkeit von 95, 47% hat (gute Passform). Oder in einer anderen Sprache wird die Information über die Y-Variable durch die X-Variable zu 95, 47% erklärt.

Der andere wichtige Teil der gesamten Ausgabe ist eine Koeffiziententabelle. Es gibt Koeffizientenwerte an, mit denen das Modell für zukünftige Vorhersagen erstellt werden kann.

Nun lautet unsere Regressionsgleichung für die Vorhersage:

Gewicht = 0, 6746 * Höhe - 38, 45508 (Steigungswert für Höhe ist 0, 6746… und Achsenabschnitt ist -38, 45508…)

Hast du bekommen, was du definiert hast? Sie haben eine Funktion definiert, in die Sie jetzt nur noch den Wert für Height eingeben müssen, und Sie erhalten den Wert für Weight.

# 2 - Regressionsanalyse mit Scatterplot mit Trendlinie in Excel

Nun werden wir sehen, wie wir in Excel eine Regressionsgleichung auf ein Streudiagramm selbst anwenden können.

• Wählen Sie Ihre gesamten Daten mit zwei Spalten (einschließlich Überschriften) aus.
• Klicken Sie auf " Einfügen" und wählen Sie " Streudiagramm" im Diagrammbereich aus, wie in der Abbildung unten dargestellt.

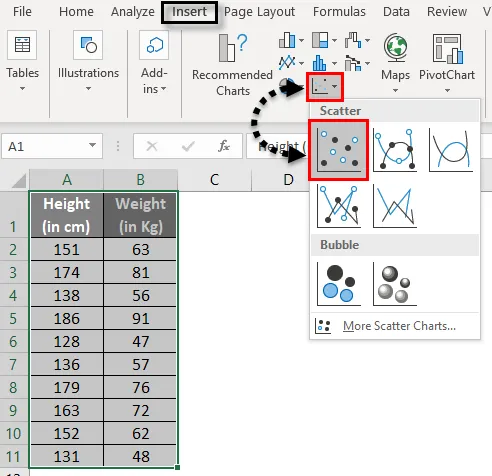
• Siehe das Ausgabediagramm.

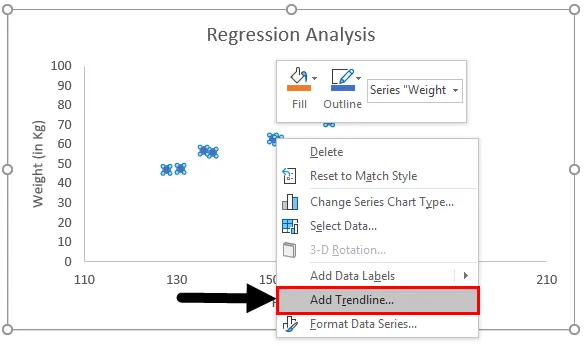
• Jetzt müssen wir eine Regressionslinie im kleinsten Quadrat in diesem Diagramm haben. Um diese Linie hinzuzufügen, klicken Sie mit der rechten Maustaste auf einen der Datenpunkte im Diagramm und wählen Sie die Option Trendlinie hinzufügen.

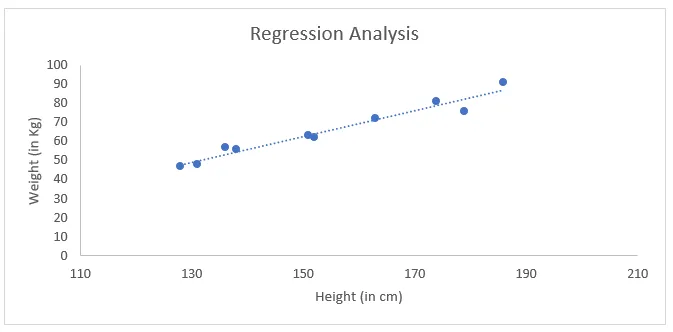
• Es ermöglicht Ihnen eine Trendlinie der kleinsten Regressionsquadrate wie unten.

• Aktivieren Sie unter der Option " Trendlinie formatieren" das Kontrollkästchen " Gleichung im Diagramm anzeigen".

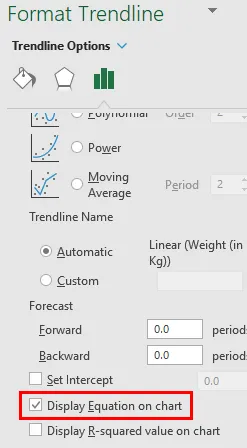
• Hiermit können Sie die Gleichung der kleinsten quadratischen Regressionsgeraden im Diagramm anzeigen.

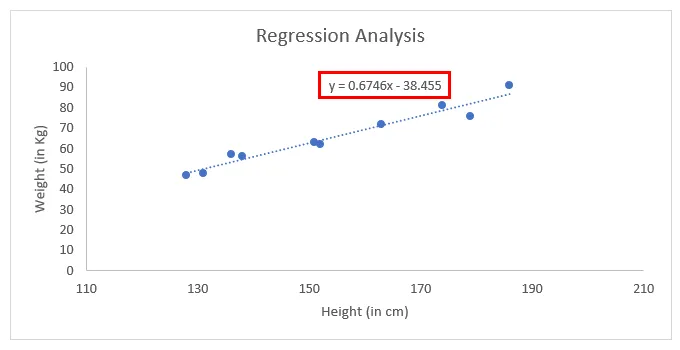
Dies ist die Gleichung, mit der wir die Gewichtswerte für einen gegebenen Satz von Höhenwerten vorhersagen können.

Wichtige Informationen zur Regressionsanalyse in Excel

• Sie können das Layout der Trendlinie unter der Option "Trendlinie formatieren" im Streudiagramm ändern.
• Es wird immer empfohlen, sich die Restdiagramme anzusehen, während Sie mit dem Data Analysis ToolPak in Excel eine Regressionsanalyse durchführen. Sie erhalten ein besseres Verständnis der Streuung der tatsächlichen Y-Werte und der geschätzten X-Werte.
• Für die einfache lineare Regression in Excel sind keine ANOVA und kein angepasstes R-Quadrat zur Überprüfung erforderlich. Diese Funktionen können für die multiple lineare Regression berücksichtigt werden. Was den Rahmen dieses Artikels sprengt.

Empfohlene Artikel

Dies war eine Anleitung zur Regressionsanalyse in Excel. Hier wird die Regressionsanalyse in Excel zusammen mit Excel-Beispielen und einer herunterladbaren Excel-Vorlage erläutert. Sie können auch unsere anderen Artikelvorschläge durchgehen -

1. Excel-Tool zur Datenanalyse
2. Berechnen Sie die ANOVA in Excel
3. So finden Sie Excel Moving Averages
4. Z TEST Beispiele in Excel