Unterschied zwischen linearer Regression und logistischer Regression
Der folgende Artikel Lineare Regression im Vergleich zur logistischen Regression zeigt die wichtigsten Unterschiede zwischen beiden. Bevor wir jedoch sehen, was Regression bedeutet.
Regression
Die Regression ist im Grunde genommen ein statistisches Maß, um die Stärke der Beziehung zwischen einer abhängigen Variablen, dh der Ausgabe Y, und einer Reihe anderer unabhängiger Variablen, dh X 1, X 2 usw., zu bestimmen. Die Regressionsanalyse wird grundsätzlich zur Vorhersage und Prognose verwendet.
Was ist lineare Regression?
Die lineare Regression ist ein Algorithmus, der auf dem überwachten Lernbereich des maschinellen Lernens basiert. Es erbt eine lineare Beziehung zwischen seinen Eingabevariablen und der einzelnen Ausgabevariablen, wobei die Ausgabevariable kontinuierlicher Natur ist. Es wird verwendet, um den Wert der Ausgabe vorherzusagen, sagen wir Y aus den Eingaben, sagen wir X. Wenn nur eine einzelne Eingabe berücksichtigt wird, spricht man von einer einfachen linearen Regression.
Es kann in zwei Hauptkategorien eingeteilt werden:
1. Einfache Regression
Funktionsprinzip: Das Hauptziel besteht darin, die Gleichung einer geraden Linie zu finden, die am besten zu den abgetasteten Daten passt. Diese Gleichung beschreibt algebraisch die Beziehung zwischen den beiden Variablen. Die am besten passende Gerade wird als Regressionsgerade bezeichnet.
Y = β 0 + β 1 X
Wo,
β repräsentiert die Merkmale
β 0 repräsentiert den Achsenabschnitt
β 1 steht für den Koeffizienten des Merkmals X
2. Multivariable Regression
Es wird verwendet, um eine Korrelation zwischen mehr als einer unabhängigen Variablen und einer abhängigen Variablen vorherzusagen. Die Regression mit mehr als zwei unabhängigen Variablen basiert auf der Anpassung der Form an die Datenkonstellation in einem mehrdimensionalen Diagramm. Die Form der Regression sollte so sein, dass der Abstand der Form von jedem Datenpunkt minimiert wird.
Ein lineares Beziehungsmodell kann wie folgt mathematisch dargestellt werden:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Wo,
β repräsentiert die Merkmale
β 0 repräsentiert den Achsenabschnitt
β 1 repräsentiert den Koeffizienten des Merkmals X 1
β n repräsentiert den Koeffizienten des Merkmals X n
Vor- und Nachteile der linearen Regression
Nachfolgend sind Vor- und Nachteile aufgeführt:
Vorteile
- Aufgrund seiner Einfachheit wird es häufig zur Modellierung von Vorhersagen und Schlussfolgerungen verwendet.
- Es konzentriert sich auf Datenanalyse und Datenvorverarbeitung. Es werden also unterschiedliche Daten verarbeitet, ohne sich um die Details des Modells zu kümmern.
Nachteile
- Es funktioniert effizient, wenn die Daten normal verteilt sind. Für eine effiziente Modellierung muss daher die Kollinearität vermieden werden.
Was ist logistische Regression?
Es ist eine Form der Regression, die die Vorhersage diskreter Variablen durch eine Mischung aus kontinuierlichen und diskreten Prädiktoren ermöglicht. Dies führt zu einer einzigartigen Transformation abhängiger Variablen, die sich nicht nur auf den Schätzprozess, sondern auch auf die Koeffizienten unabhängiger Variablen auswirkt. Es wird die gleiche Frage angesprochen, die von der multiplen Regression gestellt wird, jedoch ohne Verteilungsannahmen für die Prädiktoren. In der logistischen Regression ist die Ergebnisvariable binär. Der Zweck der Analyse besteht darin, die Auswirkungen mehrerer erklärender Variablen zu bewerten, die numerisch oder kategorisch oder beides sein können.
Arten der logistischen Regression
Nachfolgend sind die 2 Arten der logistischen Regression aufgeführt:
1. Binäre logistische Regression
Es wird verwendet, wenn die abhängige Variable dichotom ist, dh wie ein Baum mit zwei Zweigen. Es wird verwendet, wenn die abhängige Variable nicht parametrisch ist.
Wird verwendet, wenn
- Wenn es keine Linearität gibt
- Es gibt nur zwei Ebenen der abhängigen Variablen.
- Wenn multivariate Normalität zweifelhaft ist.
2. Multinomial Logistic Regression
Die multinomiale logistische Regressionsanalyse erfordert, dass die unabhängigen Variablen metrisch oder dichotom sind. Es werden keine Annahmen zur Linearität, Normalität und Homogenität der Varianz für die unabhängigen Variablen getroffen.
Es wird verwendet, wenn die abhängige Variable mehr als zwei Kategorien hat. Es wird verwendet, um Beziehungen zwischen einer nicht metrikabhängigen Variablen und metrischen oder dichotomen unabhängigen Variablen zu analysieren und dann mehrere Gruppen durch eine Kombination von binären logistischen Regressionen zu vergleichen. Am Ende wird für jeden der beiden Vergleiche eine Reihe von Koeffizienten bereitgestellt. Die Koeffizienten für die Referenzgruppe werden als Nullen angenommen. Schließlich erfolgt die Vorhersage auf der Grundlage der höchsten resultierenden Wahrscheinlichkeit.
Vorteil der logistischen Regression: Sie ist eine sehr effiziente und weit verbreitete Technik, da sie nicht viele Rechenressourcen erfordert und keine Optimierung erfordert.
Nachteil der logistischen Regression: Sie kann nicht zur Lösung nichtlinearer Probleme verwendet werden.
Head to Head Vergleich zwischen Linear Regression und Logistic Regression (Infographics)
Nachfolgend sind die sechs wichtigsten Unterschiede zwischen linearer und logistischer Regression aufgeführt 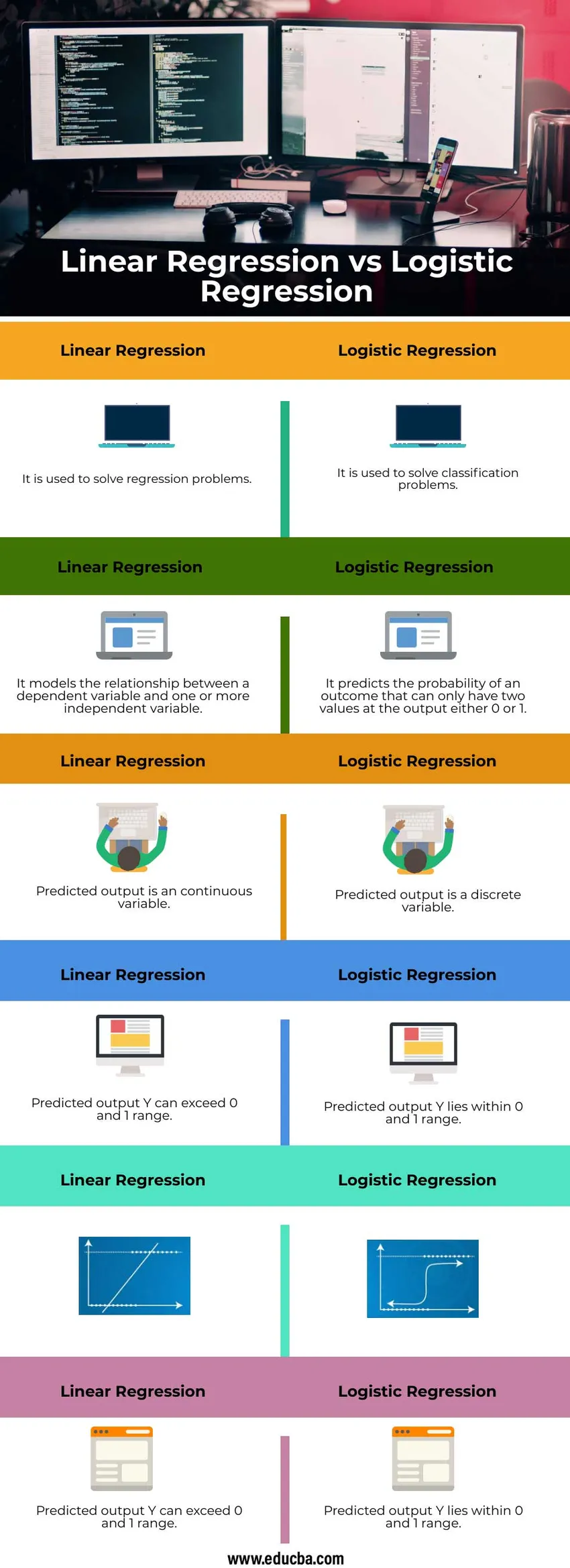
Hauptunterschied zwischen der linearen Regression und der logistischen Regression
Lassen Sie uns einige der wichtigsten Unterschiede zwischen linearer und logistischer Regression diskutieren
Lineare Regression
- Es ist ein linearer Ansatz
- Es wird eine gerade Linie verwendet
- Es können keine kategorialen Variablen verwendet werden
- Beobachtungen mit fehlenden Werten der numerischen unabhängigen Variablen müssen ignoriert werden
- Ausgang Y ist gegeben als
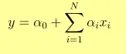
- 1 Einheitserhöhung in x erhöht Y um α
Anwendungen
- Vorhersage des Produktpreises
- Vorhersage der Punktzahl in einem Spiel
Logistische Regression
- Es ist ein statistischer Ansatz
- Es verwendet eine Sigmoid-Funktion
- Es können kategoriale Variablen verwendet werden
- Es kann Entscheidungen treffen, auch wenn Beobachtungen mit fehlenden Werten vorliegen
- Ausgang Y ist gegeben als, wobei z gegeben ist als
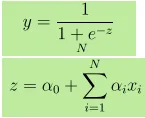
- Eine Erhöhung von x um 1 Einheit erhöht Y um die logarithmische Wahrscheinlichkeit von α
- Wenn P die Wahrscheinlichkeit eines Ereignisses ist, dann ist (1-P) die Wahrscheinlichkeit, dass es nicht auftritt. Erfolgsaussichten = P / 1-P
Anwendungen
- Vorhersage, ob es heute regnen wird oder nicht.
- Vorhersage, ob es sich bei einer E-Mail um Spam handelt oder nicht.
Lineare Regression vs Logistische Regression Vergleichstabelle
Lassen Sie uns den besten Vergleich zwischen linearer Regression und logistischer Regression diskutieren
|
Lineare Regression |
Logistische Regression |
| Es wird verwendet, um Regressionsprobleme zu lösen | Es wird verwendet, um Klassifizierungsprobleme zu lösen |
| Es modelliert die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen | Sie sagt die Wahrscheinlichkeit eines Ergebnisses voraus, das am Ausgang entweder 0 oder 1 nur zwei Werte haben kann |
| Die vorhergesagte Ausgabe ist eine kontinuierliche Variable | Die vorhergesagte Ausgabe ist eine diskrete Variable |
| Der vorhergesagte Ausgang Y kann den Bereich 0 und 1 überschreiten | Das vorhergesagte Ausgangssignal Y liegt im Bereich von 0 bis 1 |
 | 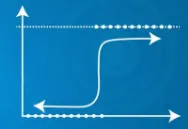 |
| Der vorhergesagte Ausgang Y kann den Bereich 0 und 1 überschreiten | Voraussichtliche Ausgabe |
Fazit
Wenn Features nicht zur Vorhersage beitragen oder wenn sie stark miteinander korrelieren, wird das Modell verrauscht. Daher müssen Features entfernt werden, die nicht genug zum Modell beitragen. Wenn unabhängige Variablen stark korreliert sind, kann dies zu einem Problem der Multi-Kollinearität führen, das durch Ausführen separater Modelle mit jeder unabhängigen Variablen gelöst werden kann.
Empfohlene Artikel
Dies war ein Leitfaden für die lineare Regression im Vergleich zur logistischen Regression. Hier werden die Hauptunterschiede zwischen linearer Regression und logistischer Regression mit Infografiken und die Vergleichstabelle erörtert. Weitere Informationen finden Sie auch in den folgenden Artikeln.
- Data Science vs Datenvisualisierung
- Maschinelles Lernen vs Neuronales Netz
- Betreutes Lernen gegen tiefes Lernen
- Logistische Regression in R