
Varianzanalyseformel (Inhaltsverzeichnis)
- Formel
- Beispiele
Was ist die Varianzanalyseformel?
Die Varianzanalyse ist eine wichtige Formel für das Portfoliomanagement und andere Finanz- und Geschäftsanalysen. Die quantitative Formel kann als Differenz zwischen geplanten und tatsächlichen Zahlen gemessen werden. Die Formel wird häufig in der Kostenanalyse verwendet, um die Abweichung zwischen den geplanten oder den Standardkosten und den tatsächlichen Kosten zu überprüfen. Die Analyse hilft dem Management, die operative Leistung des Unternehmens zu überprüfen.
Die Formel für die Varianzanalyse ist unten angegeben
Variance = (X – µ) 2 / N
- X steht für den Wert eines einzelnen Datenpunktes
- µ steht für den Durchschnitt oder den Mittelwert des einzelnen Datenpunktes
- N steht für die Anzahl der einzelnen Datenpunkte in einem bestimmten Array
Die Varianzanalyseformel wird in einer Wahrscheinlichkeitsverteilung verwendet, und die Varianz wird auch als Maß für das Risiko aus einem Durchschnittsmittelwert definiert. Die Varianz zeigt auch, inwieweit der Anleger das Risiko beim Kauf eines bestimmten Wertpapiers übernehmen kann.
Beispiele für eine Varianzanalyseformel (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung der Varianzanalyse besser zu verstehen.
Sie können diese Excel-Vorlage für die Varianzanalyseformel hier herunterladen - Excel-Vorlage für die VarianzanalyseformelVarianzanalyseformel - Beispiel # 1
Betrachten Sie einen Datensatz mit den folgenden Beobachtungen 2, 3, 6, 6, 7, 2, 1, 2, 8. Wir müssen die Varianzanalyse berechnen.
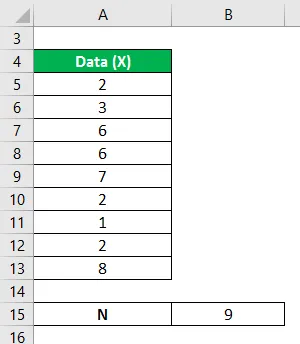
Die Lösung für das folgende Problem kann durch Ausführen der folgenden Schritte erreicht werden:
Mittelwert wird berechnet als:

Jetzt müssen wir die Differenz zwischen den Datenpunkten und dem Mittelwert berechnen.
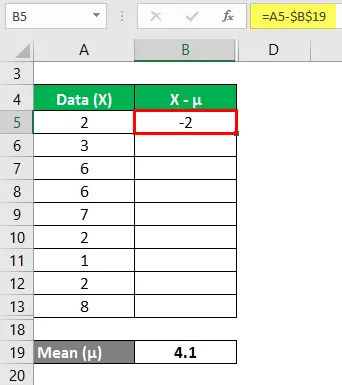
Berechnen Sie in ähnlicher Weise für alle Werte des Datensatzes.
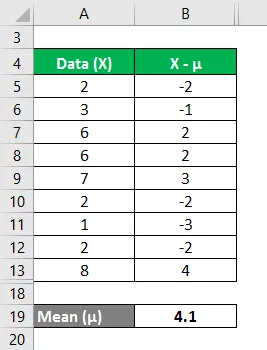
Berechnen Sie das Quadrat der Differenz zwischen Datenpunkten und dem Mittelwert.
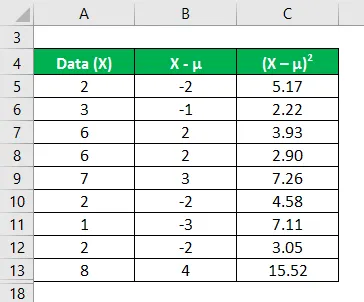
Die Varianzanalyse wird mit der unten angegebenen Formel berechnet
Varianz = (X - u) 2 / N
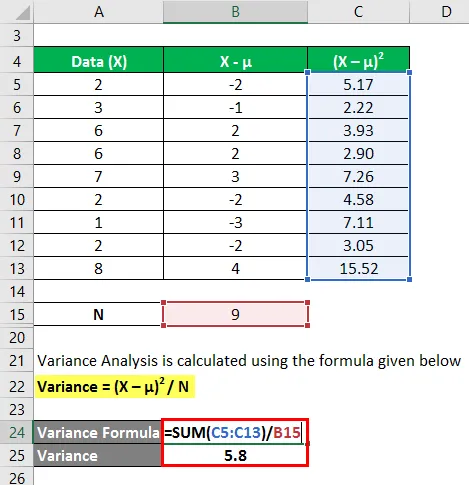
Im ersten Schritt haben wir den Mittelwert durch Summieren (2 + 3 + 6 + 6 + 7 + 2 + 1 + 2 + 8) / Anzahl der Beobachtungen berechnet, was einen Mittelwert von 4, 1 ergibt. Dann haben wir in Spalte 2 die Differenz zwischen den Datenpunkten und dem Mittelwert berechnet und jeden Wert einzeln quadriert. Nach dieser Summierung von Spalte C und Division durch die Anzahl der Beobachtungen ergibt sich die Varianz von 5, 8.
Varianzanalyseformel - Beispiel 2
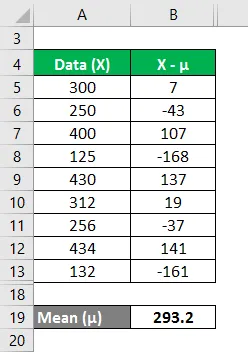
Die Höhen der Hunde in einem gegebenen Satz einer Zufallsvariablen betragen 300 mm, 250 mm, 400 mm, 125 mm, 430 mm, 312 mm, 256 mm, 434 mm und 132 mm. Berechnen Sie die Varianzanalyse des Datensatzes aus dem Mittelwert.
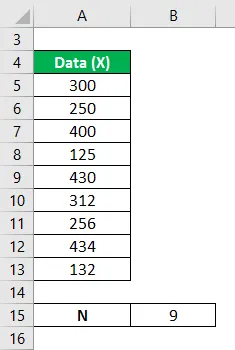
Die Lösung für das folgende Problem kann durch Ausführen der folgenden Schritte erreicht werden:
Mittelwert wird berechnet als:
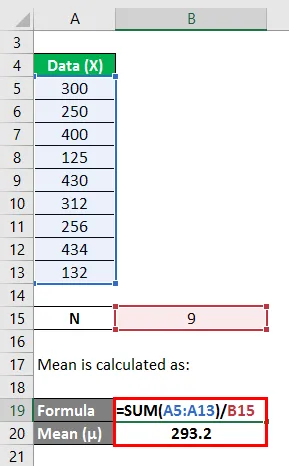
Jetzt müssen wir die Differenz zwischen den Datenpunkten und dem Mittelwert berechnen.
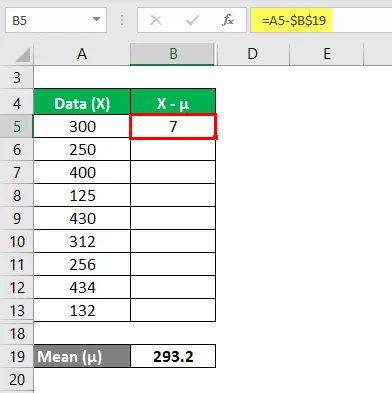
Berechnen Sie in ähnlicher Weise für alle Werte des Datensatzes.
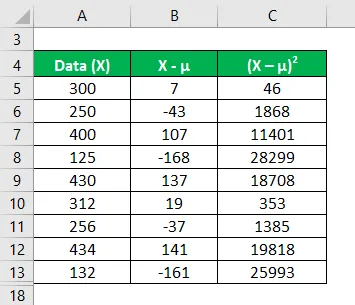
Berechnen Sie das Quadrat der Differenz zwischen Datenpunkten und dem Mittelwert.
Die Varianzanalyse wird mit der unten angegebenen Formel berechnet
Varianz = (X - u) 2 / N
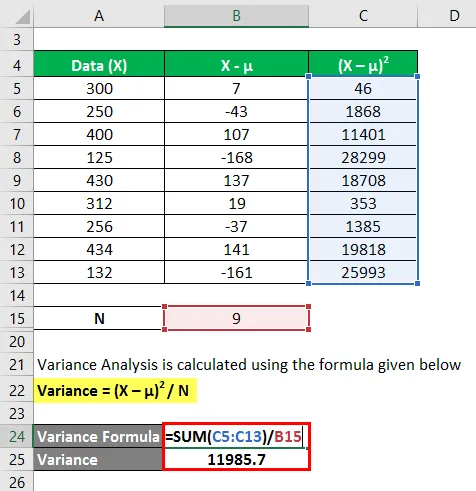
Im ersten Schritt haben wir den Mittelwert durch Summieren (300 + 250 + 400 + 125 + 430 + 312 + 256 + 434 + 132) / Anzahl der Beobachtungen berechnet, was einen Mittelwert von 293, 2 ergibt. Dann haben wir in Spalte 2 die Differenz zwischen den Datenpunkten und dem Mittelwert berechnet und jeden Wert einzeln quadriert. Nach der Summierung von Spalte C und Division durch die Anzahl der Beobachtungen ergibt sich die Varianz von 11985.7.
Varianzanalyseformel - Beispiel # 3
Die Noten der Schüler, die aus einer großen Stichprobe von 100 Schülern ausgewählt wurden, sind 12, 15, 18, 24, 36, 10. Berechnen Sie die Varianzanalyse der Daten aus dem Mittelwert.
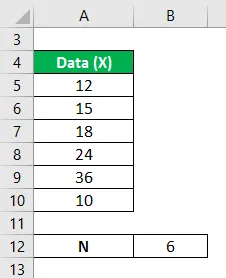
Die Lösung für das folgende Problem kann durch Ausführen der folgenden Schritte erreicht werden:
Mittelwert wird berechnet als:

Jetzt müssen wir die Differenz zwischen den Datenpunkten und dem Mittelwert berechnen.
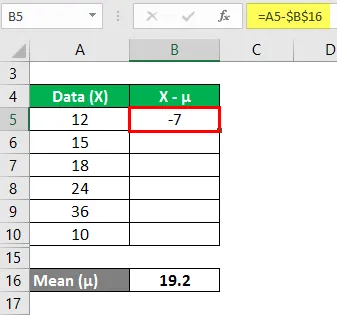
Berechnen Sie in ähnlicher Weise für alle Werte des Datensatzes.
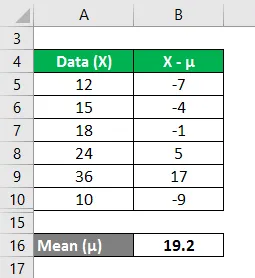
Berechnen Sie das Quadrat aus der Differenz der Datenpunkte und dem Mittelwert.
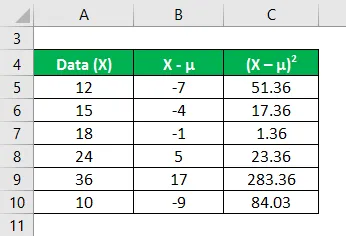
Die Varianzanalyse wird mit der unten angegebenen Formel berechnet
Varianz = (X - u) 2 / N
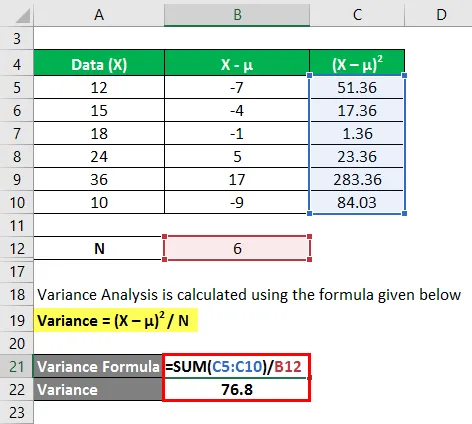
Im ersten Schritt haben wir den Mittelwert durch Summieren (12 + 15 + 18 + 24 + 36 + 10) / Anzahl der Beobachtungen berechnet, was einen Mittelwert von 19, 2 ergibt. Dann haben wir in Spalte 2 die Differenz zwischen den Datenpunkten und dem Mittelwert berechnet und jeden Wert einzeln quadriert. Nach der Summierung von Spalte C und Division durch die Anzahl der Beobachtungen ergibt sich die Varianz von 76, 8
Erläuterung
Die Varianzanalyseformel wird in folgenden Schritten berechnet:
Schritt 1: Berechnen Sie den Mittelwert der Anzahl der im Datenfeld vorhandenen Beobachtungen, den Sie mit einer einfachen Mittelwertformel berechnen können, die die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen ist.
Schritt 2: Nach der Berechnung des Mittelwerts der Beobachtungen wird jede Beobachtung vom Mittelwert subtrahiert, um die Abweichung jeder Beobachtung vom Mittelwert zu berechnen.
Schritt 3: Die Differenz jeder Beobachtung wird dann summiert und quadriert, um die negativ-positive Beschilderung zu vermeiden, und dann durch die Anzahl der Beobachtungen dividiert.
Relevanz und Verwendung der Varianzanalyseformel
Die Varianzanalyse kann in folgenden Bereichen eingesetzt werden:
- Portfolio-Management
- Berechnung der Aktien- und Portfoliorendite
- Budget vs. Ist-Kosten-Vergleich, der im Geschäft sehr häufig verwendet wird
- Kosten- und Ertragsprognose
- Wesentlichkeit
- Beziehungen zwischen zwei Variablen
Empfohlene Artikel
Dies war ein Leitfaden für die Varianzanalyseformel. Hier diskutieren wir, wie die Varianzanalyse berechnet wird, zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Prozentuale Fehlerformel mit Taschenrechner
- Beispiele für Regressionsformeln mit Excel-Vorlage
- Was ist die relative Standardabweichungsformel?
- Wie berechnet man die Korrelation?