
Quartilformel (Inhaltsverzeichnis)
- Formel
- Beispiele
Definition der Quartilformel
Quartil ist, wie der Name schon sagt, ein statistischer Begriff, der die Daten in Viertel oder vier definierte Intervalle unterteilt. Grundsätzlich werden die Datenpunkte in einen Datensatz unterteilt, der auf der Zahlenlinie in vier Viertel unterteilt ist. Eine Sache, die wir berücksichtigen müssen, ist, dass Datenpunkte zufällig sein können, und wir müssen diese Zahlen zuerst in aufsteigender Reihenfolge in die Zahlenreihe einreihen und sie dann in Quartile unterteilen. Es ist im Grunde eine erweiterte Version des Medians. Der Median teilt die Daten in zwei gleiche Teile, die die Quartile in vier Teile teilen. Sobald wir die Daten teilen, werden die vier Quartile sein:
- Das 1. Quartil oder das untere Quartil unterscheidet grundsätzlich die niedrigsten 25% der Daten von den höchsten 75%.
- 2. Quartil oder mittleres Quartil, auch Median genannt, teilt Zahlen in 2 gleiche Teile.
- Das dritte Quartil oder das obere Quartil trennen die höchsten 25% der Daten von den niedrigsten 75%.
Formel für Quartil:
Angenommen, wir haben einen Datensatz mit N Datenpunkten:
X - (X1, X2, X3 ……… .. XN)
Die Formel für Quartile ist gegeben durch:
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Lower Quartile (Q1) = (N+1) * 1 / 4 Middle Quartile (Q2) = (N+1) * 2 / 4 Upper Quartile (Q3 )= (N+1) * 3 / 4 Interquartile Range = Q3 – Q1
Was es im Grunde bedeutet, ist, dass in einem Datensatz mit N Datenpunkten:
((N + 1) * 1/4). Term ist das untere Quartil
((N + 1) * 2/4). Term ist das mittlere Quartil
((N + 1) * 3/4). Term ist das obere Quartil
Interquartilreichweite grundsätzlich Abstände zwischen Unterquartil und Oberquartil.
Beispiele für Quartilformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des Quartils besser zu verstehen.
Sie können diese Excel-Vorlage für Quartilformeln hier herunterladen - Excel-Vorlage für QuartilformelnQuartilformel - Beispiel # 1
Angenommen, wir haben einen Datensatz A, der 19 Datenpunkte enthält. Berechnen Sie das Quartil für Datensatz A.
Datensatz:
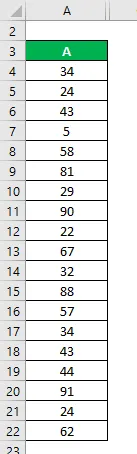
Zunächst müssen Sie diese aufsteigende Reihenfolge einordnen, dh von der niedrigsten zur höchsten:
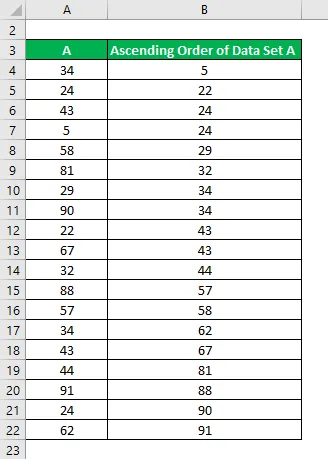
Anzahl der Datenpunkte wird berechnet als:
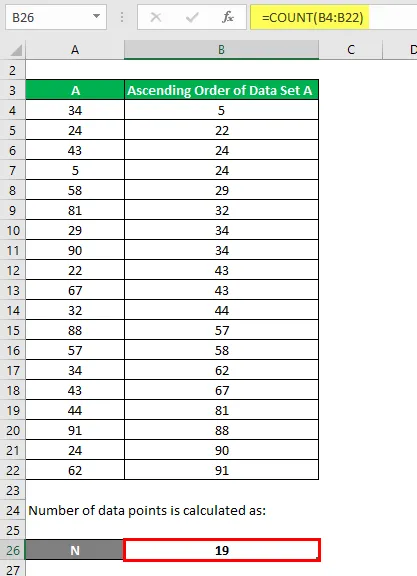
Das Quartil wird nach der unten angegebenen Formel berechnet
Unteres Quartil (Q1) = (N + 1) * 1/4
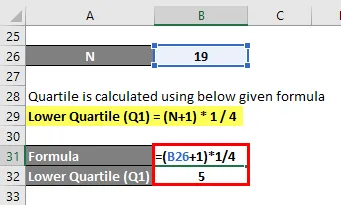
- Unteres Quartil (Q1) = (19 + 1) * 1/4
- Unteres Quartil (Q1) = 20/4 = 5. Datenpunkt
Also unteres Quartil (Q1) = 29
Mittleres Quartil (Q2) = (N + 1) * 2/4

- Mittleres Quartil (Q2) = (19 + 1) * 2/4
- Mittleres Quartil (Q2) = 40/4 = 10. Datenpunkt
Also mittleres Quartil (Q2) = 43
Oberes Quartil (Q3) = (N + 1) * 3/4

- Oberes Quartil (Q3) = (19 + 1) * 3/4
- Oberes Quartil (Q3) = 60/4 = 15. Datenpunkt
Also oberes Quartil (Q3) = 67
Der Interquartilbereich wird mit der unten angegebenen Formel berechnet
Interquartilbereich = Q3 - Q1
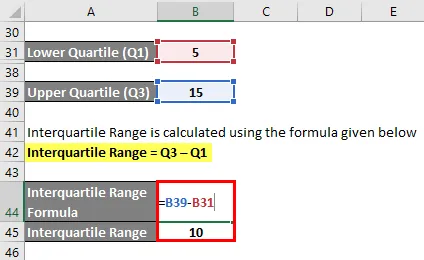
- Interquartilbereich = 15–5
- Interquartilbereich = 10. Datenpunkt
Interquartilbereich = 43
Wenn Sie den Datensatz sehen, ist der Median dieses Satzes: (n + 1) / 2 = 20/2 = 10. Wert, dh 43, dies ist dasselbe wie bei Q2.
Inferenz:
- Der Wert 29 teilt den Datensatz so auf, dass die niedrigsten 25% darüber und die höchsten 75% darunter liegen
- Der Wert 43 teilt den Datensatz in zwei gleiche Teile
- Der Wert 67 teilt den Datensatz so auf, dass die höchsten 25% darunter und die niedrigsten 75% darüber liegen
Quartilformel - Beispiel # 2
Sehen wir uns ein weiteres Beispiel an, wie Unternehmen und Unternehmen mit diesem Tool eine fundierte Entscheidung treffen können, welches Produkt produziert werden soll.
Angenommen, Sie sind ein Hersteller von Laufschuhen und eine bekannte Marke unter den Athleten, die einen Marathon laufen, Sport treiben usw. Sie haben die Daten der Schuhgrößen gesammelt, die diese Athleten tragen, damit Sie in Zukunft mehr von dieser Größe produzieren die Nachfrage befriedigen.
Sie haben eine Stichprobe von 15 Athleten aus verschiedenen Sportarten gesammelt. Berechnen Sie das Quartil.
Der Datensatz ist unten angegeben:
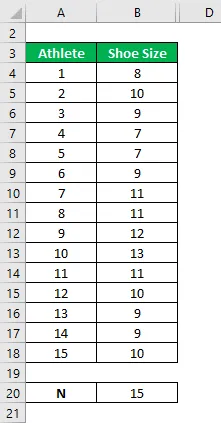
Ordnen Sie die Schuhgröße in aufsteigender Reihenfolge.
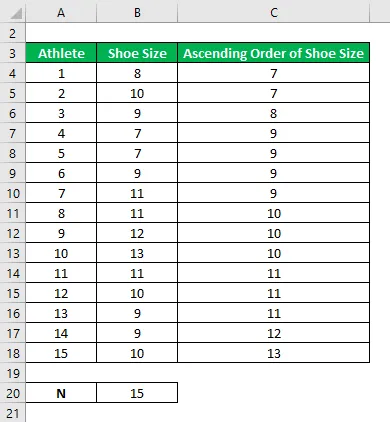
Das Quartil wird nach der unten angegebenen Formel berechnet
Unteres Quartil (Q1) = (N + 1) * 1/4
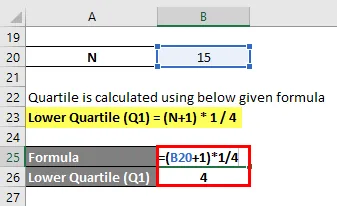
- Unteres Quartil (Q1) = (15 + 1) * 1/4
- Unteres Quartil (Q1) = 16/4 = 4. Datenpunkt
Also unteres Quartil (Q1) = 10
Mittleres Quartil (Q2) = (N + 1) * 2/4
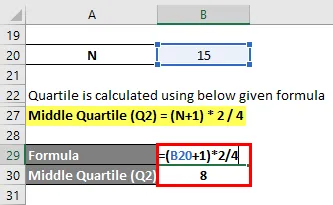
- Mittleres Quartil (Q2) = (15 + 1) * 2/4
- Mittleres Quartil (Q2) = 32/4 = 8. Datenpunkt
Also mittleres Quartil (Q2) = 10
Oberes Quartil (Q3) = (N + 1) * 3/4

- Oberes Quartil (Q3) = (15 + 1) * 3/4
- Oberes Quartil (Q3) = 48/4 = 12. Datenpunkt
Also oberes Quartil (Q3) = 11
Der Interquartilbereich wird mit der unten angegebenen Formel berechnet
Interquartilbereich = Q3 - Q1
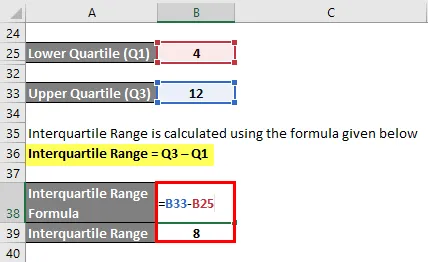
- Interquartilbereich = 12 - 4
- Interquartilbereich = 8. Datenpunkt
Also Interquartilbereich = 10
Erläuterung
Um die Quartile besser zu verstehen, müssen wir den Median besser verstehen. Der Median teilt den Datensatz in genau zwei gleiche Hälften, sagt aber nichts über die Verbreitung der Daten auf beiden Seiten aus. Ein Quartil ist eine erweiterte Version davon und durch Teilen des Datensatzes in vier Teile wird die Verteilung der Werte über und unter dem Mittelwert behandelt. Es gibt auch andere statistische Tools, die uns Auskunft über den Umfang des Datensatzes, die Mitte des Datensatzes usw. geben. Die Quartilformel hilft uns jedoch, all diese Elemente zu verstehen. Das mittlere Quartil gibt den Mittelpunkt und das obere und untere Quartil die Ausbreitung an.
Relevanz und Verwendung der Quartilformel
Wie oben erläutert, hilft uns die Quartilformel dabei, die Daten sehr schnell in vier Teile zu unterteilen, und erleichtert uns schließlich das Verständnis der Daten in diesen Teilen. Zum Beispiel möchte ein Klassenlehrer die besten 25% der Schüler mit Geschenken und Geschenken belohnen und eine weitere Chance geben, 25% der Schüler zu unterbieten, um ihre Punktzahl zu verbessern. Er kann Quartile verwenden und die Daten teilen. Wenn also die Quartile 51, 65, 72 lauten und die Punktzahl eines Schülers 78 lautet, erhält er Goodies. Wenn ein anderer Schüler eine Punktzahl von 48 hat, wird er eine weitere Chance haben, die Punktzahl zu verbessern und schnell und einfach zu interpretieren.
Empfohlene Artikel
Dies war ein Leitfaden für die Quartilformel. Hier diskutieren wir die Definition und Berechnung des Quartils zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Beispiele für Ausreißerformeln (Excel-Vorlage)
- Rechner für Perzentilrangformel
- Formel zur Berechnung des angepassten R-Quadrats
- Wie berechne ich die Binomialverteilung?
- Quartilabweichungsformel | Beispiele | Taschenrechner