
Einführung in Merge Sort in JavaScript
Sortieralgorithmen sind in der Informatik sehr wichtig. Die Ausgabe der Sortierung besteht darin, die Elemente einer Liste in einer bestimmten Reihenfolge anzuordnen (entweder aufsteigend oder absteigend). Sortieren in JavaScript zusammenführen ist einer der effizientesten verfügbaren Sortieralgorithmen, da er auf dem Konzept von Teilen und Erobern basiert. Teilen Sie, wie der Name schon sagt, zunächst das größere Problem in kleine Probleme auf, bevor Sie die kleineren Probleme lösen, um das größere Problem zu lösen. Konzeptionell ist Merge Sort eine Kombination aus zwei grundlegenden Algorithmen namens MERGE und MERGE_SORT.
was wie folgt funktioniert:
- Teilen Sie die unsortierte Liste in n Unterlisten mit einzelnen Elementen auf (n ist die Gesamtzahl der Elemente in der unsortierten Liste).
- Führe Unterlisten wiederholt zu sortierten Unterlisten zusammen, bis es nur noch eine sortierte Liste gibt.
Implementierung von Merge Sort in JavaScript
Der MERGE-Algorithmus folgt der Prozedur des Kombinierens von zwei sortierten Listen zu einer sortierten Liste.
Beispiel: Angenommen, es gibt zwei Listen, dh Liste 1 (1, 5, 3) und Liste 2 (7, 2, 9).
1. Sortieren Sie zuerst beide Listen.
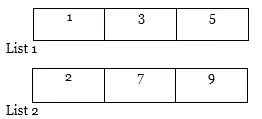
Nun werden wir die E-Technik sehen und darauf anwenden.
2. Dann erstellen wir eine neue Liste mit der Größe x + y, wobei x die Anzahl der Elemente in Liste 1 und y die Anzahl der Elemente in Liste 2 ist.

In unserem Fall ist x = 3 und y = 3, also ist x + y = 6.
3. Nun haben wir zwei Zeiger.
Ein erster Zeiger, der auf die erste Position von Liste 1 zeigt, und ein zweiter Zeiger, der auf die erste Position von Liste 2 zeigt.

4. Dann vergleichen wir den Wert beider Zeiger. Den Zeiger mit kleinerem Wert kopieren Sie dieses Element in Liste 3 und bewegen Sie den Zeiger rechts von der Liste mit kleinerem Wert und der resultierenden Liste (dh Liste 1 und Liste 3).

5. Führen Sie Schritt 4 auf ähnliche Weise immer wieder aus.

Weiterfahrt… ..
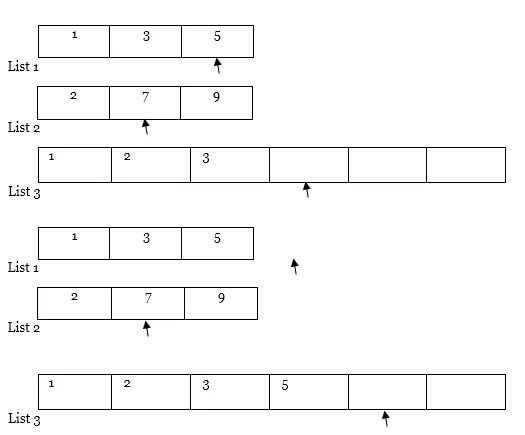
Hinweis : Wenn eine der Listen (dh Liste 1 oder Liste 2) wie im Fall vollständig durchlaufen wird, kopieren Sie den gesamten Inhalt einer anderen Liste wie folgt vom Zeiger in die Ergebnisliste (dh Liste 3).

Pseudocode
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
Der MERGE_SORT-Algorithmus teilt die angegebene unsortierte Liste auf die Mindestgröße auf und ruft dann den MERGE-Algorithmus auf, um die Liste in die neue sortierte Liste zu kombinieren.
Pseudocode
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Beispiel
Hier folgen wir der top-down Merge Sort Implementierung. Es beginnt oben und geht nach unten, wobei bei jeder rekursiven Runde die gleiche Frage gestellt wird: "Was muss getan werden, um die Liste zu sortieren?" Ergebnisse".
Code in Javascript
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Die Hauptfunktion der Zusammenführungssortierung teilt die angegebene Liste in jeder Iteration des rekursiven Aufrufs in kleinere Listen auf. Vergessen Sie nicht, dass eine Rekursion die Grundbedingung erfordert, um eine unendliche Rekursion zu vermeiden. In unserem Fall haben wir:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Nachdem wir die Grundbedingung für die Rekursion festgelegt haben, identifizieren wir den mittleren Index, um die angegebene Liste in die linke und rechte Unterliste aufzuteilen, wie Sie oben im Beispieldiagramm sehen können. Dann müssen wir die linke Unterliste und die rechte Unterliste zusammenführen, nach denen wir jetzt suchen. In der Zusammenführungsfunktion oben müssen wir sicherstellen, dass wir alle Elemente in der linken Unterliste und der rechten Unterliste sortieren. aufführen. Wir verwenden dazu eine while-Schleife. Innerhalb der while-Schleife vergleichen wir das Element in der linken Unterliste und das Element in der rechten Unterliste nacheinander. Wir können den kleineren von beiden in die Ergebnisliste schieben und den Cursor der linken und rechten Unterliste entsprechend bewegen. Schließlich müssen wir die Ergebnisliste verketten. Dies ist sehr wichtig! Wenn wir diesen letzten Schritt hier nicht ausführen, wird am Ende eine unvollständige Liste von Elementen angezeigt, da die while-Schleifenbedingung fehlschlägt, sobald einer der beiden Zeiger das Ende erreicht.
Ausgabe:

Eigenschaften der Zusammenführungssortierung
- Die Zusammenführungssortierung ist stabil, da dasselbe Element in einem Array seine ursprünglichen Positionen in Bezug aufeinander beibehält.
- Die Zusammenführungssortierung ist nicht vorhanden, da beim Zusammenführen eine Kopie der gesamten Liste sortiert wird. Aus diesem Grund ist die Platzkomplexität (O (n)) dieses Algorithmus tatsächlich größer als bei anderen Algorithmen und sollte nicht bei komplexen Problemen verwendet werden, bei denen der Platz knapp ist.
- Die Gesamtzeitkomplexität der Zusammenführungssortierung ist O (nLogn). Es ist effizienter als im schlimmsten Fall, die Laufzeit ist O (nlogn).
Fazit
Die besten, schlechtesten und durchschnittlichen Zeitkomplexitäten der Zusammenführungssortierung sind gleich, wodurch der Algorithmus effizienter wird. Es funktioniert schneller als andere Sortiertechniken. Die Zusammenführungssortierung kann auf Dateien beliebiger Größe angewendet werden. Es ist aufgrund der Verwendung der Divide-and-Conquer-Methode in hohem Maße parallelisierbar. Um fundierte Grundlagen in der Informatik zu entwickeln, sollten Sie die verschiedenen Sortieralgorithmen gründlich verstehen.
Empfohlener Artikel
Dies war eine Anleitung zum Zusammenführen der Sortierung in JavaScript. Hier diskutieren wir die Einführung in Merge Sort in JavaScript und die Implementierung zusammen mit den Eigenschaften. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren -
- JavaScript-Mathematikfunktionen
- Einführung in JavaScript
- Beste Javascript Frameworks
- JavaScript-Werkzeuge
- Top 6 Sortieralgorithmus in JavaScript