Was ist GLM in R?
Verallgemeinerte lineare Modelle sind eine Teilmenge der linearen Regressionsmodelle und unterstützen Nicht-Normalverteilungen effektiv. Um dies zu unterstützen, wird empfohlen, die Funktion glm () zu verwenden. GLM funktioniert gut mit einer Variablen, wenn die Varianz nicht konstant und normal verteilt ist. Eine Verknüpfungsfunktion wird definiert, um die Antwortvariable an das entsprechende Modell anzupassen. Ein LM-Modell wird sowohl mit der Familie als auch mit der Formel erstellt. Das GLM-Modell besteht aus drei Schlüsselkomponenten: Zufall (Wahrscheinlichkeit), Systematisch (linearer Prädiktor) und Link-Komponente (für die Logit-Funktion). Der Vorteil der Verwendung von glm besteht darin, dass sie über Modellflexibilität verfügen und keine konstante Varianz erfordern. Dieses Modell entspricht der Schätzung der maximalen Wahrscheinlichkeit und ihren Verhältnissen. In diesem Thema lernen wir GLM in R kennen.
GLM-Funktion
Syntax: glm (Formel, Familie, Daten, Gewichte, Teilmenge, Start = Null, Modell = WAHR, Methode = ””…)
Hier umfassen Familientypen (einschließlich Modelltypen) Binomial, Poisson, Gauß, Gamma und Quasi. Jede Distribution führt eine andere Verwendung durch und kann sowohl für die Klassifizierung als auch für die Vorhersage verwendet werden. Und wenn das Modell Gauß ist, sollte die Antwort eine echte ganze Zahl sein.
Und wenn das Modell binomial ist, sollte die Antwort Klassen mit binären Werten sein.
Und wenn das Modell Poisson ist, sollte die Antwort mit einem numerischen Wert nicht negativ sein.
Und wenn das Modell Gamma ist, sollte die Antwort ein positiver numerischer Wert sein.
glm.fit () - So passen Sie ein Modell an
Lrfit () - bezeichnet die logistische Regressionsanpassung.
update () - Hilft beim Aktualisieren eines Modells.
anova () - es ist ein optionaler Test.
Wie erstelle ich GLM in R?
Hier wird gezeigt, wie mit der Funktion glm () ein einfaches verallgemeinertes lineares Modell mit Binärdaten erstellt wird. Und indem Sie mit dem Datensatz Bäume fortfahren.
Beispiele
// Eine Bibliothek importierenlibrary(dplyr)
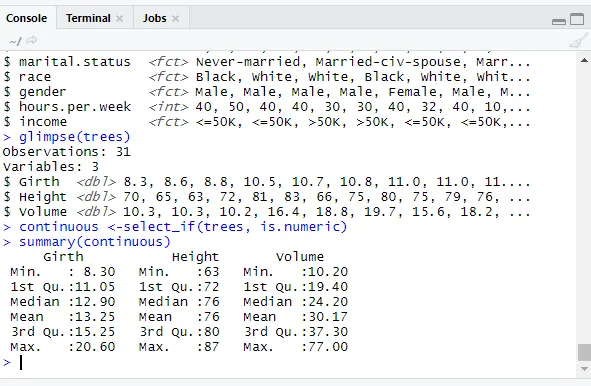
glimpse(trees)

Um kategoriale Werte zu sehen, werden Faktoren zugewiesen.
levels(factor(trees$Girth))
// Kontinuierliche Variablen überprüfen
library(dplyr)
continuous <-select_if(trees, is.numeric)
summary(continuous)
// Baumdatensatz in R-Suche einbinden Pathattach (Bäume)
x<-glm(Volume~Height+Girth)
x
Ausgabe:
| Aufruf: glm (Formel = Volumen ~ Höhe + Umfang)
Koeffizienten: (Abfangen) Höhe Umfang -57, 9877 0, 3393 4, 7082 Freiheitsgrade: 30 insgesamt (dh Null); 28 Rest Null-Abweichung: 8106 Restabweichung: 421, 9 AIC: 176, 9 |
summary(x)
| Anruf:
glm (Formel = Volumen ~ Höhe + Umfang) Abweichungsreste: Min 1Q Median 3Q Max -6.4065 -2.6493 -0.2876 2.2003 8.4847 Koeffizienten: Schätzung Std. Fehler t Wert Pr (> | t |) (Abschnitt) -57, 9877 8, 6382 -6, 713 2, 75e-07 Höhe 0.3393 0.1302 2.607 0.0145 * Umfang 4, 7082 0, 2643 17, 816 <2e-16 *** - Signif. Codes: 0 "***" 0, 001 "**" 0, 01 "*" 0, 05 ". 0, 1 '' 1 (Dispersionsparameter für die Gauß-Familie als 15, 06862 angenommen) Nullabweichung: 8106.08 bei 30 Freiheitsgraden Restabweichung: 421, 92 bei 28 Freiheitsgraden AIC: 176, 91 Anzahl der Fisher-Scoring-Iterationen: 2 |
Die Ausgabe der Zusammenfassungsfunktion gibt die Aufrufe, Koeffizienten und Residuen aus. Die obige Antwort zeigt, dass sowohl der Höhen- als auch der Umfangskoeffizient nicht signifikant sind, da ihre Wahrscheinlichkeit weniger als 0, 5 beträgt. Und es gibt zwei Varianten von Abweichungen mit dem Namen null und residual. Schließlich ist Fisher Scoring ein Algorithmus, der Probleme mit maximaler Wahrscheinlichkeit löst. Bei Binomial ist die Antwort ein Vektor oder eine Matrix. cbind () wird verwendet, um die Spaltenvektoren in einer Matrix zu binden. Und um die detaillierten Informationen der Anpassung zu erhalten, wird die Zusammenfassung verwendet.
To do Like Hood Test wird der folgende Code ausgeführt.
step(x, test="LRT")
Start: AIC=176.91
Volume ~ Height + Girth
Df Deviance AIC scaled dev. Pr(>Chi)
421.9 176.91
- Height 1 524.3 181.65 6.735 0.009455 **
- Girth 1 5204.9 252.80 77.889 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Call: glm(formula = Volume ~ Height + Girth)
Coefficients:
(Intercept) Height Girth
-57.9877 0.3393 4.7082
Degrees of Freedom: 30 Total (ie Null); 28 Residual
Null Deviance: 8106
Residual Deviance: 421.9 AIC: 176.9
Modell passen
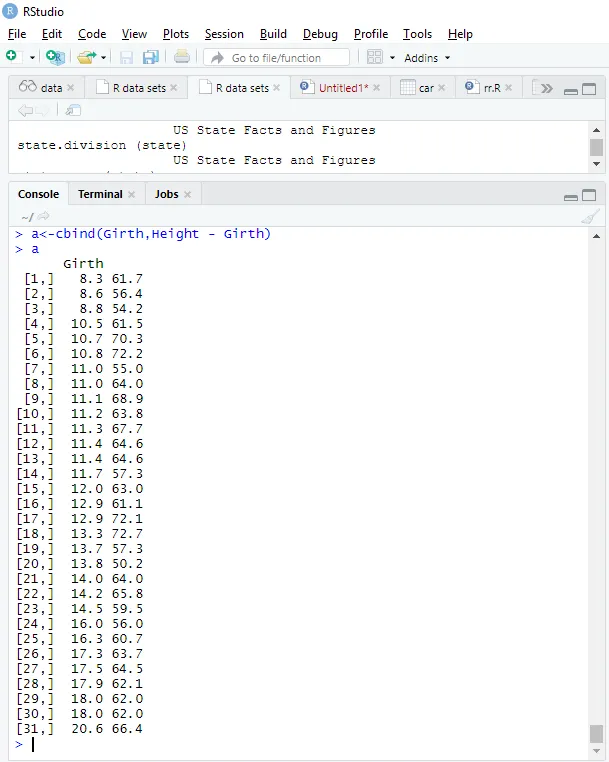
a<-cbind(Height, Girth - Height)
> a
Zusammenfassung (Bäume)
Girth Height Volume
Min. : 8.30 Min. :63 Min. :10.20
1st Qu.:11.05 1st Qu.:72 1st Qu.:19.40
Median :12.90 Median :76 Median :24.20
Mean :13.25 Mean :76 Mean :30.17
3rd Qu.:15.25 3rd Qu.:80 3rd Qu.:37.30
Max. :20.60 Max. :87 Max. :77.00
Um die entsprechende Standardabweichung zu erhalten
apply(trees, sd)
Girth Height Volume
3.138139 6.371813 16.437846
predict <- predict(logit, data_test, type = 'response')
Als Nächstes beziehen wir uns auf die Antwortvariable count, um eine gute Antwortanpassung zu modellieren. Um dies zu berechnen, verwenden wir den USAccDeath-Datensatz.
Geben Sie die folgenden Ausschnitte in die R-Konsole ein und sehen Sie, wie die Jahreszählung und das Jahresquadrat für sie ausgeführt werden.
data("USAccDeaths")
force(USAccDeaths)
// Das Jahr von 1973-1978 analysieren.
disc <- data.frame(count=as.numeric(USAccDeaths), year=seq(0, (length(USAccDeaths)-1), 1)))
yearSqr=disc$year^2
a1 <- glm(count~year+yearSqr, family="poisson", data=disc)
summary(a1)
| Anruf:
glm (Formel = count ~ year + yearSqr, Familie = "poisson", Daten = disc) Abweichungsreste: Min 1Q Median 3Q Max -22.4344 -6.4401 -0.0981 6.0508 21.4578 Koeffizienten: Schätzung Std. Fehler z Wert Pr (> | z |) (Abschnitt) 9, 187e + 00 3, 557e - 03 2582, 49 <2e - 16 Jahr -7.207e-03 2.354e-04 -30.62 <2e-16 Jahr 8, 841e-05 3, 221e-06 27, 45 <2e-16 *** - Signif. Codes: 0 "***" 0, 001 "**" 0, 01 "*" 0, 05 ". 0, 1 '' 1 (Dispersionsparameter für die Poisson-Familie als 1 angenommen) Nullabweichung: 7357, 4 bei 71 Freiheitsgraden Restabweichung: 6358, 0 bei 69 Freiheitsgraden AIC: 7149, 8 Anzahl der Fisher-Scoring-Iterationen: 4 |
Um die beste Übereinstimmung des Modells zu überprüfen, kann der folgende Befehl verwendet werden
die Reste für den Test. Aus dem folgenden Ergebnis ergibt sich der Wert 0.
1 - pchisq(deviance(a1), df.residual(a1))
Verwendung der QuasiPoisson-Familie für die größere Varianz in den angegebenen Daten
a2 <- glm(count~year+yearSqr, family="quasipoisson", data=disc)
summary(a2)
| Anruf:
glm (Formel = Anzahl ~ Jahr + JahrSqr, Familie = "Quasipoisson", data = disc) Abweichungsreste: Min 1Q Median 3Q Max -22.4344 -6.4401 -0.0981 6.0508 21.4578 Koeffizienten: Schätzung Std. Fehler t Wert Pr (> | t |) (Abfangen) 9, 187e + 00 3, 417e-02 268, 822 <2e-16 Jahr -7.207e-03 2.261e-03 -3.188 0.00216 ** Jahr 8, 841e-05 3, 095e-05 2, 857 0, 00565 ** - (Dispersionsparameter für die Quasipoisson-Familie als 92, 28857 angenommen) Nullabweichung: 7357, 4 bei 71 Freiheitsgraden Restabweichung: 6358, 0 bei 69 Freiheitsgraden AIC: NA Anzahl der Fisher-Scoring-Iterationen: 4 |
Der Vergleich von Poisson mit dem binomialen AIC-Wert unterscheidet sich erheblich. Sie können nach Genauigkeit und Rückrufquote analysiert werden. Im nächsten Schritt wird überprüft, ob die Varianz der Residuen proportional zum Mittelwert ist. Dann können wir mithilfe der ROCR-Bibliothek zeichnen, um das Modell zu verbessern.
Fazit
Daher haben wir uns auf ein spezielles Modell konzentriert, das als verallgemeinertes lineares Modell bezeichnet wird und bei der Fokussierung und Schätzung der Modellparameter hilft. Es ist in erster Linie das Potenzial für eine kontinuierliche Antwortvariable. Und wir haben gesehen, wie glm zu einem R-Einbaupaket passt. Sie sind die beliebtesten Ansätze zum Messen von Zähldaten und ein robustes Werkzeug für Klassifizierungstechniken, die von einem Datenwissenschaftler verwendet werden. Die R-Sprache hilft natürlich bei der Ausführung komplizierter mathematischer Funktionen
Empfohlene Artikel
Dies ist eine Anleitung zu GLM in R. Hier werden die GLM-Funktion und das Erstellen von GLM in R anhand von Beispielen und Ausgaben für Baumdatensätze erläutert. Sie können auch den folgenden Artikel lesen, um mehr zu erfahren -
- R Programmiersprache
- Big Data-Architektur
- Logistische Regression in R
- Big Data Analytics-Jobs
- Poisson-Regression in R | Implementierung der Poisson-Regression