
Einführung in die rekursive Funktion in Java
Eine rekursive Funktion ist diejenige, die sich selbst ein- oder mehrmals aufruft. Eine rekursive Funktion wird in Situationen verwendet, in denen derselbe Satz von Operationen immer wieder ausgeführt werden muss, bis das Ergebnis erreicht ist. Es werden mehrere Iterationen ausgeführt, und die problem-Anweisung wird mit jeder Iteration einfacher.
Beim Schreiben einer rekursiven Funktion muss immer ein Basislimit angegeben werden, da dies sonst zu einem Stapelüberlauffehler führt. Ein Stapel ist ein Speicherbereich, der zur Verwaltung von Methodenaufrufen reserviert ist. Der Fehler besteht darin, dass die Funktion fortlaufend ausgeführt wird, da sie die Grenzbedingung nicht finden kann und somit den zugewiesenen Speicherplatz endgültig erschöpft. Um einen Stapelüberlauf zu verhindern, definieren wir bestimmte Basisbedingungen mit Hilfe von „if… else“ -Anweisungen (oder anderen bedingten Anweisungen), die die Rekursionsfunktion anhalten lassen, sobald die erforderliche Berechnung abgeschlossen ist.
Arten der Rekursion in Java
In Java gibt es zwei Arten der Rekursion. Sie sind:
1. Direkte Rekursion
Syntax:
Hier ruft sich die Funktion1 kontinuierlich auf und ist daher eine rekursive Funktion.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Beispiel
Die Fakultät einer Zahl ist ein Beispiel für eine direkte Rekursion. Das Grundprinzip der Rekursion besteht darin, ein komplexes Problem durch Aufteilen in kleinere zu lösen. Zum Beispiel berechnen wir im Fall der Fakultät einer Zahl die Fakultät von „i“, wenn wir die Fakultät von „i-1“ kennen.
Code:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Ausgabe:

2. Indirekte / gegenseitige Rekursion
Eine Funktion1, die eine andere Funktion2 aufruft, die wiederum direkt oder indirekt die Funktion1 aufruft, wird als indirekte rekursive Funktion bezeichnet.
Syntax:
Betrachten Sie 2 Funktionen mit den Namen function1 () und function2 (). Hier ruft function1 function2 und function2 function1 auf.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Beispiel
Um die indirekte Rekursion zu zeigen, verwenden wir das folgende Programm, um herauszufinden, ob eine gegebene Zahl aus der gegebenen Eingabe gerade oder ungerade ist.
Code:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Ausgabe:
Beispiele für die Rekursion in Java
Im Folgenden finden Sie einige weitere Beispiele zur Lösung der Probleme mithilfe der Rekursionsmethode.
Beispiel # 1 - Fibonacci-Sequenz
Eine Menge von "n" Zahlen wird als Fibonacci-Folge bezeichnet, wenn Nummer3 = Nummer1 + Nummer2, dh jede Nummer ist eine Summe der beiden vorhergehenden Zahlen. Daher beginnt die Sequenz immer mit den ersten beiden Ziffern wie 0 und 1. Die dritte Ziffer ist eine Summe aus 0 und 1, was zu 1 führt, die vierte Ziffer ist die Addition von 1 und 1, was zu 2 führt, und die Sequenz geht weiter.
Überprüfen Sie den folgenden Code in Java, um eine Fibonacci-Sequenz zu generieren:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Ausgabe:

Hier werden die ersten beiden Ziffern mit 0 und 1 initialisiert und ausgedruckt. Mit den Variablen „num1“, „num2“ und „num3“ wird die gewünschte Sequenz generiert. Die Variable “num3” erhält man durch Addition von “num1” und “num2” und die Zahlen werden durch Mischen um eine Position nach links verschoben, wie im Code gezeigt. Die Funktion „Fibonacci“ wird hier rekursiv aufgerufen und bei jeder Iteration wird der Wert von „n“ um 1 verringert. Daher wird die Rekursion beendet, sobald „n“ den Wert 0 erreicht.
Beispiel # 2 - Turm von Hanoi
Dies ist ein klassisches mathematisches Problem, bei dem es sich um 3-polige und "n" Festplatten unterschiedlicher Größe handelt. Das Puzzle sieht wie folgt aus:
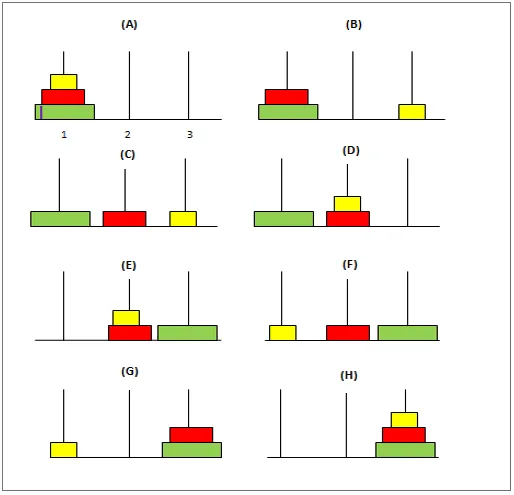
Zu Beginn werden die Scheiben auf der ersten Stange so angeordnet, dass die größte Scheibe unten und die kleinste oben auf der Stange liegt. Das Ziel ist es, diese Scheiben vom ersten zum dritten Pol zu bewegen, wobei die Scheiben in der gleichen Position wie in der ersten Position gehalten werden. Im Folgenden sind einige Bedingungen aufgeführt, die beim Verschieben dieser Datenträger zu beachten sind:
1. Es muss immer nur eine Platte verschoben werden.
2. Dabei ist es nicht zulässig, eine größere Festplatte über eine kleinere zu legen.
3. Der zweite (mittlere) Pol kann zum Vermitteln verwendet werden, während die Scheiben vom ersten auf den zweiten Pol übertragen werden.
Im Folgenden finden Sie den Java-Code, mit dem Sie das Rätsel lösen können:
Code:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Ausgabe:
Hier steht die Variable "count" für die Anzahl der zu verwendenden Disks. Die Funktion „Turm“ ist die rekursive Funktion, mit der die Scheiben von Stange 1 zu Stange 3 bewegt werden. Eine einfache Lösung für dieses Problem kann darin bestehen, zunächst zwei Scheiben zu betrachten.
- Zuerst bewegen wir die Scheibe 1 von Stab 1 zu Stab 2.
- Als nächstes bewegen wir Scheibe 2 zu Stange 3.
- Zum Schluss bewegen wir die Scheibe 1 zum Stab 3, um die gewünschte Lösung zu erhalten.
Dasselbe Prinzip wird für die Anzahl „n“ der Scheiben angewendet, indem die Scheibe von Stab 1 nach 2 bewegt wird (n-1) und ähnliche Schritte wie oben ausgeführt werden.
Vorteile der Rekursion in Java
- Der Code ist einfach zu schreiben und zu pflegen.
- Die beste Methode, um die Ergebnisse zu finden, wenn eine große Anzahl von Iterationen erforderlich ist.
Nachteile der Rekursion in Java
- Rekursive Funktionen belegen mehr Speicher. Dies liegt daran, dass jedes Mal eine rekursive Funktion aufgerufen wird. Die Speicherzuordnung wird für die Variablen auf dem Stapel neu vorgenommen. Und die entsprechende Speicherzuordnung wird freigegeben, sobald die Variablenwerte zurückgegeben werden.
- Dieser Vorgang der Speicherzuweisung dauert länger, daher ist die Ausführung normalerweise langsam.
Fazit
Rekursive Funktionen sind relativ einfach zu codieren, aber sie sind im Vergleich zu den anderen vorhandenen Methoden auch nicht so effizient. Daher werden sie hauptsächlich in Fällen verwendet, in denen die für die Entwicklung vorgegebene Zeit geringer ist und auch ein signifikantes Muster in dem Problem beobachtet werden kann.
Empfohlene Artikel
Dies ist eine Anleitung zur Rekursion in Java. Hier diskutieren wir die Arten der Rekursion in Java zusammen mit ihren verschiedenen Beispielen mit den Vor- und Nachteilen. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren.
- JScrollPane in Java
- Mathematikfunktionen in Java
- Mathematikfunktionen in Java
- Konstruktor in Java
- Rekursive Funktion in Python
- Factorial-Programm in JavaScript