
Einführung in Standardabweichungsbeispiele
Es gibt zahlreiche Beispiele für Standardabweichungen. Die Standardabweichung ist das Maß für die Streuung des Datensatzes, dh wie verteilt die Zahlen sind. Es ist nützlich, um die verschiedenen Datensätze zu vergleichen, die den gleichen Mittelwert, aber den unterschiedlichen Bereich haben können. Das folgende Beispiel für unterschiedliche Standardabweichungen gibt einen Überblick über die häufigsten Situationen, in denen die Standardabweichung berechnet wird und wie diese berechnet werden kann
Beispiele für Standardabweichungen
Nachfolgend finden Sie Beispiele für die Standardabweichung
Standardabweichung - Beispiel # 1
Die Aktie von Unternehmen Z verkauft sich für 50 USD pro Aktie und bietet für das nächste Jahr die folgenden Auszahlungen:
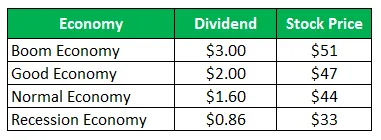
Berechnen Sie die Standardabweichung, wenn alle vier Szenarien gleich wahrscheinlich sind.
Lösung:
Berechnungen der Haltedauer Rendite (HPR) sind wie folgt:
Formel von HPR
HPR = ((Periodenendwert - Ursprünglicher Wert) + Einkommen) / Ursprünglicher Wert) * 100
Für eine boomende Wirtschaft
- HPR (Ausleger) = ((51-50) + 3) / 50 = 8, 00%
- HPR (gut) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (Rezession) = ((33-50) + 0, 86) / 50 = -32, 28%
Berechnung der erwarteten Rendite
Da alle Szenarien gleich wahrscheinlich sind, beträgt die Wahrscheinlichkeit für alle ¼
Formel der erwarteten Rendite
Erwartete Rendite = (Wahrscheinlichkeit des Aufschwungs * Rückkehr vom Aufschwung) + (Wahrscheinlichkeit des Guten * Rückkehr vom Guten) + (Wahrscheinlichkeit des Normalen * Rückkehr vom Normalen) + (Wahrscheinlichkeit der Rezession * Rückkehr von der Rezession)
- Erwartete Rendite = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Erwartete Rendite = -8, 77%
Berechnung der Standardabweichung
Formel der Varianz
Varianz = (Wahrscheinlichkeit eines Booms * (Rendite aus dem Boom - erwartete Gesamtrendite) 2) + (Wahrscheinlichkeit eines Guten * (Rendite aus dem Guten - erwartete Gesamtrendite) 2) + (Wahrscheinlichkeit eines Normalen * (Rendite aus dem Normalen - erwartete Gesamtrendite) 2 ) + (Rezessionswahrscheinlichkeit * (Rückkehr aus der Rezession - erwartete Gesamtrendite) 2)
- Varianz = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varianz = 219, 95
Formel der Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz
Standardabweichung = √Varianz
- Standardabweichung = √ 219, 95
- Standardabweichung = 14, 83%
Beispiel für Standardabweichung - 2
Standardabweichung bei zwei Unternehmen im Portfolio
Die Stammaktien von Unternehmen A werden für 28 USD je Aktie verkauft und die gleichen Angebote nach den Auszahlungen für das nächste Jahr

Die Stammaktien von Unternehmen B werden für 93 US-Dollar je Aktie verkauft und bieten für das nächste Jahr die folgenden Auszahlungen:

(a) Berechnen Sie die Standardabweichung von Unternehmen A
(b) Berechnen Sie die Standardabweichung von Unternehmen B
(c) Berechnen Sie die Standardabweichung des Portfolios, wenn die Hälfte der Investition bei Unternehmen A und die andere Hälfte bei Unternehmen B getätigt wird
Lösung:
Für Firma A
Berechnungen der Haltedauer Rendite (HPR)
Formel von HPR
HPR = ((Periodenendwert - Ursprünglicher Wert) + Einkommen) / Ursprünglicher Wert) * 100
- HPR (Ausleger) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (Rezession) = ((38-28) + 5) / 28 = 53, 57%
Berechnung der erwarteten Rendite von Unternehmen A
Formel der erwarteten Rendite
Erwartete Rendite = (Wahrscheinlichkeit des Booms * Rückkehr vom Boom) + (Wahrscheinlichkeit des Normalen * Rückkehr vom Normalen) + (Wahrscheinlichkeit der Rezession * Rückkehr von der Rezession)
- Erwartete Rendite = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Erwartete Rendite = 3, 84%
Berechnung der Standardabweichung Firma A
Formel der Varianz
Varianz = (Boomwahrscheinlichkeit * (Boomrendite - erwartete Gesamtrendite) 2) + (Normalwahrscheinlichkeit * (Normalrendite - erwartete Gesamtrendite) 2 ) + (Rezessionswahrscheinlichkeit * (Rezessionsrendite - erwartete Gesamtrendite) 2)
- Varianz = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varianz = 895, 15
Formel der Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz
Standardabweichung = √Varianz
- Standardabweichung = √ 895, 15
- Standardabweichung = 29, 92%
Für Firma B
Berechnungen der Haltedauer Rendite (HPR)
Formel von HPR
HPR = ((Periodenendwert - Ursprünglicher Wert) + Einkommen) / Ursprünglicher Wert) * 100
HPR (Ausleger) = ((200-93) +7) / 93 = 122, 58%
HPR (normal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (Rezession) = ((4-93) +2) / 93 = -93, 55%
Berechnung der erwarteten Rendite
Formel der erwarteten Rendite
Erwartete Rendite = (Wahrscheinlichkeit des Booms * Rückkehr vom Boom) + (Wahrscheinlichkeit des Normalen * Rückkehr vom Normalen) + (Wahrscheinlichkeit der Rezession * Rückkehr von der Rezession)
- Erwartete Rendite = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Erwartete Rendite = 43, 04%
Berechnung der Standardabweichung
Formel der Varianz
Varianz = (Boomwahrscheinlichkeit * (Boomrendite - erwartete Gesamtrendite) 2) + (Normalwahrscheinlichkeit * (Normalrendite - erwartete Gesamtrendite) 2 ) + (Rezessionswahrscheinlichkeit * (Rezessionsrendite - erwartete Gesamtrendite) 2)
- Varianz = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (–93, 55– (43, 04)) 2
- Varianz = 6783, 65
Formel der Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz
Standardabweichung = √Varianz
- Standardabweichung = 6783, 65
- Standardabweichung = 82, 36%
Berechnung der erwarteten Rendite und Standardabweichung eines Portfolios, das zur Hälfte in Unternehmen A und zur Hälfte in Unternehmen B investiert ist
Standardabweichung von Unternehmen A = 29, 92%
Standardabweichung von Unternehmen B = 82, 36%
Gewicht der Firma A = 0, 50
Gewicht der Firma B = 0, 50
Die Formel der Standardabweichung des Portfolios
Standardabweichung des Portfolios = (Gewicht von Unternehmen A * Erwartete Rendite von Unternehmen A) + ((Gewicht von Unternehmen B * Erwartete Rendite von Unternehmen B)
- Standardabweichung des Portfolios = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardabweichung des Portfolios = 56, 14%
Analyse
Die Standardabweichung des Portfolios ist geringer als für die einzelnen Aktien, da die Aktien in verschiedene Aktien diversifiziert sind. Die Diversifikation führt zu einer Reduzierung des Risikos, sofern nicht eine perfekte Korrelation zwischen den Renditen der Portfolioinvestitionen besteht.
Schlussfolgerung - Beispiele für Standardabweichungen
Die Standardabweichung misst die Streuung des Datensatzes relativ zum Mittelwert. Es wird als Quadratwurzel der Varianz berechnet. Je größer die Standardabweichung des Wertpapiers ist, desto größer ist die Varianz zwischen dem Preis und dem Mittelwert, was zeigt, dass die Preisspanne groß ist. Die oben genannten Beispiele sind einige Beispiele für die Standardabweichung auf unterschiedliche Weise. Es gibt auch verschiedene andere Beispiele, die zeigen, dass die Standardabweichung unter Verwendung anderer Daten berechnet werden kann.
Empfohlene Artikel
Dies war eine Anleitung zu den Standardabweichungsbeispielen. Hier diskutieren wir die verschiedenen Beispiele der Standardabweichung zusammen mit einer detaillierten Erklärung . Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Beispiel für Fixkosten
- Beispiel für variable Kosten
- Quantitatives Forschungsbeispiel
- Monopolistische Wettbewerbsbeispiele