
Einführung in die einfache lineare Regression
Aus dem Wörterbuch : Eine Rückkehr in einen früheren oder weniger entwickelten Zustand.
In der Statistik: Ein Maß für die Beziehung zwischen dem Mittelwert einer Variablen und den entsprechenden Werten der anderen Variablen.
Die Regression, bei der die Beziehung zwischen der Eingangsvariablen (unabhängige Variable) und der Zielvariablen (abhängige Variable) als linear betrachtet wird, wird als lineare Regression bezeichnet. Einfache lineare Regression ist eine Art der linearen Regression, bei der wir nur eine unabhängige Variable haben, um die abhängige Variable vorherzusagen. Einfache lineare Regression ist einer der Algorithmen für maschinelles Lernen. Einfache lineare Regression gehört zur Familie des betreuten Lernens. Die Regression wird zur Vorhersage kontinuierlicher Werte verwendet.
Modell der einfachen linearen Regression
Machen wir es uns einfach. Wie alles begann?
Begonnen hat alles 1800 mit Francis Galton. Er studierte die Beziehung zwischen Vätern und ihren Söhnen in der Höhe. Er beobachtete ein Muster: Entweder wäre die Größe des Sohnes so groß wie die Größe seines Vaters oder die Größe des Sohnes entspricht eher der durchschnittlichen Größe aller Menschen. Dieses Phänomen ist nichts als Regression.
Zum Beispiel ist Shaq O'Neal ein sehr berühmter NBA-Spieler und 2, 16 Meter groß. Seine Söhne Shaqir und Shareef O'neal sind 1, 96 m bzw. 2, 06 m groß. Die durchschnittliche Bevölkerungsgröße beträgt 1, 76 Meter. Die Körpergröße des Sohnes verringert sich (driftet) in Richtung der mittleren Körpergröße.
Wie machen wir Regression?
Berechnung einer Regression mit nur zwei Datenpunkten:
Alles, was wir tun möchten, um die beste Regression zu finden, ist, eine Linie zu zeichnen, die so nah wie möglich an jedem Punkt ist. Bei zwei Datenpunkten ist es einfach, eine Linie zu zeichnen. Verbinden Sie sie einfach.
Wenn wir nun eine Anzahl von Datenpunkten haben, wie man die Linie zeichnet, die so nah wie möglich an jedem einzelnen Datenpunkt liegt.
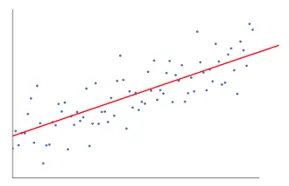
In diesem Fall ist es unser Ziel, den vertikalen Abstand zwischen der Linie und allen Datenpunkten zu minimieren. Auf diese Weise können wir die beste Linie für unser lineares Regressionsmodell vorhersagen.
Was ist die einfache lineare Regression?
Nachfolgend finden Sie eine detaillierte Erläuterung der einfachen linearen Regression:
- Es zeichnet viele, viele mögliche Linien und führt dann eine dieser Analysen durch.
- Summe der Fehlerquadrate.
- Summe der absoluten Fehler.
- Methode der kleinsten Quadrate usw
- Für unsere Analyse verwenden wir die Methode der kleinsten Quadrate.
- Wir werden alle Punkte unterscheiden und das Quadrat der Summe aller Punkte berechnen. Welche Zeile die minimale Summe angibt, ist unsere beste Zeile.
Zum Beispiel: Auf diese Weise könnten wir mehrere Männer und die Größe ihres Sohnes nehmen und beispielsweise einem Mann sagen, wie groß sein Sohn sein könnte. bevor er überhaupt geboren wurde.
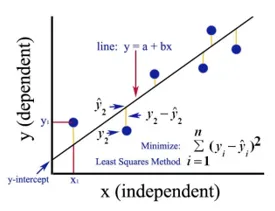
Google Bild
Die obige Abbildung zeigt eine einfache lineare Regression. Die Linie repräsentiert die Regressionslinie. Gegeben durch: y = a + b * x
Wobei y die abhängige Variable (DV) ist: Zum Beispiel, wie sich das Gehalt einer Person in Abhängigkeit von der Anzahl der Jahre Erfahrung des Mitarbeiters ändert. Hier ist also das Gehalt eines Mitarbeiters oder einer Person Ihre abhängige Variable.
Die abhängige Variable ist unsere Zielvariable, die wir mithilfe der linearen Regression vorhersagen möchten.
x ist unsere unabhängige Variable (IV): Die abhängige Variable ist die Ursache für die Änderung der unabhängigen Variablen. Im obigen Beispiel ist die Anzahl der Jahre der Erfahrung unsere abhängige Variable, da die Anzahl der Jahre der Erfahrung die Änderung des Gehalts des Mitarbeiters verursacht.
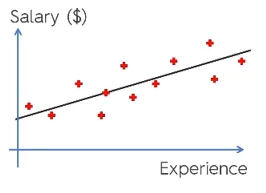
- b ist die Koeffizientenvariable für unsere unabhängige Variable x. Dieser Koeffizient spielt eine entscheidende Rolle. Hier steht, wie sich eine Änderung der Einheit in x (IV) auf y (DV) auswirkt. Es wird auch als Proportionalitätskoeffizient bezeichnet. In Bezug auf die Mathematik liegt es an Ihnen, die Steigung der Linie oder die Steilheit der Linie zu bestimmen.
- Wenn in unserem Beispiel die Steigung (b) geringer ist, bedeutet dies, dass die Anzahl der Jahre weniger Gehaltszuwächse ergibt, wenn die Steigung (b) höher ist, führt dies zu einer starken Gehaltserhöhung mit einer Erhöhung der Gehaltszuwächse langjährige Erfahrung.
- a ist ein konstanter Wert. Es wird auch als Schnittpunkt bezeichnet, dh dort, wo die Linie die y-Achse oder die DV-Achse schneidet. Auf andere Weise können wir sagen, wenn ein Mitarbeiter über null Jahre Erfahrung verfügt (x), dass das Gehalt (y) für diesen Mitarbeiter konstant ist (a).
Wie funktioniert der Least Square?
Unten sind die Punkte für die Arbeit mit den kleinsten Quadraten aufgeführt:
- Entsprechend den Datentrends wird eine willkürliche Linie gezogen.
- Es nimmt Datenpunkte auf und zeichnet vertikale Linien. Der vertikale Abstand wird als Parameter betrachtet.
- Diese vertikalen Linien schneiden die Regressionslinie und geben den entsprechenden Punkt für Datenpunkte an.
- Es wird dann die vertikale Differenz zwischen jedem Datenpunkt und seinem entsprechenden Datenpunkt auf der Regressionsgeraden ermittelt.
- Es wird der Fehler berechnet, der das Quadrat der Differenz ist.
- Anschließend wird die Summe der Fehler berechnet.
- Dann zeichnet es wieder eine Linie und wiederholt den obigen Vorgang noch einmal.
- Auf diese Weise werden mehrere Linien gezeichnet, und die Linie mit der geringsten Fehlersumme wird als beste Linie ausgewählt.
- Diese beste Linie ist unsere einfache lineare Regressionslinie.
Anwendung der einfachen linearen Regression
Eine Regressionsanalyse wird durchgeführt, um die kontinuierliche Variable vorherzusagen. Die Regressionsanalyse hat eine Vielzahl von Anwendungen. Einige Beispiele sind wie folgt:
- Predictive Analytics
- Wirksamkeit des Marketings,
- Preisgestaltung für einen Eintrag
- Werbevorhersage für ein Produkt.
Hier werden wir eine Anwendung der linearen Regression für die prädiktive Analytik diskutieren. Wir werden mit Python modellieren.
Die folgenden Schritte werden zum Erstellen unseres Modells ausgeführt:
- Wir werden die Bibliotheken und Datensätze importieren.
- Wir werden die Daten vorverarbeiten.
- Wir werden die Daten in das Test-Set und das Training-Set aufteilen.
- Wir werden ein Modell erstellen, das versucht, die Zielvariable basierend auf unserem Trainingssatz vorherzusagen
- Wir werden die Zielvariable für den Testsatz vorhersagen.
- Wir werden die vom Modell vorhergesagten Ergebnisse analysieren
Für unsere Analyse verwenden wir einen Gehaltsdatensatz mit den Daten von 30 Mitarbeitern.
# Importieren der Bibliotheken
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importieren des Datensatzes (Datenbeispiel ist in der Tabelle dargestellt)
dataset = pd.read_csv('Salary_Data.csv')
| Langjährige Erfahrung | Gehalt |
| 1.5 | 37731 |
| 1.1 | 39343 |
| 2.2 | 39891 |
| 2 | 43525 |
| 1.3 | 46205 |
| 3.2 | 54445 |
| 4 | 55749 |
# Vorverarbeitung des Datensatzes. Hier werden wir den Datensatz in die abhängige Variable und die unabhängige Variable aufteilen. x als unabhängige und y als abhängige oder Zielvariable
X = dataset.iloc(:, :-1).values
y = dataset.iloc(:, 1).values
# Aufteilen des Datensatzes in den Trainingssatz und den Testsatz:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1/3, random_state = 0)
Hier zeigt die Testgröße 1/3, dass aus den Gesamtdaten 2/3 für das Training des Modells und 1/3 für das Testen des Modells verwendet werden.
# Passen wir unser einfaches lineares Regressionsmodell an das Trainingsset an
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
Das lineare Regressionsmodell ist jetzt trainiert. Dieses Modell wird zur Vorhersage der abhängigen Variablen verwendet.
# Vorhersage der Testergebnisse
y_pred = regressor.predict(X_test)
# Visualisierung der Testergebnisse
plt.scatter(X_test, y_test, color = 'blue')
plt.plot(X_train, regressor.predict(X_train), color = 'red')
plt.title('Salary of Employee vs Experience (Test set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()
# Parameter des Modells
print(regressor.intercept_)
print(regressor.coef_)
26816.19224403119
(9345.94244312)
Der Interceptor (a) -Wert ist also 26816. Dies deutet darauf hin, dass jeder frischere (null Erfahrung) ungefähr 26816 als Gehalt erhalten würde.
Der Koeffizient für unser Modell betrug 9345, 94. Es wird vorgeschlagen, dass die Änderung einer Einheit der unabhängigen Variablen (Expositionsjahre) bei Konstanthaltung aller anderen Parameter zu einer Änderung des Gehalts um 9345 Einheiten führt.
Bewertungsmetriken für die Regression
Für die Regressionsanalyse stehen grundsätzlich 3 wichtige Bewertungsmetriken zur Verfügung:
- Mean Absolute Error (MAE): Zeigt den Mittelwert der absoluten Fehler an, bei dem es sich um die Differenz zwischen vorhergesagtem und tatsächlichem Fehler handelt.
- Mean Squared Error (MSE): Zeigt den Mittelwert der quadratischen Fehler an.
- Root Mean Squared Error (RMSE): Zeigt die Quadratwurzel des Mittelwerts der quadratischen Fehler.
Wir können die oben genannten Methoden vergleichen:
- MAE: Es zeigt den durchschnittlichen Fehler und die einfachste aller drei Methoden.
- MSE: Diese ist populärer als MAE, weil sie die größeren Fehler verstärkt, was zu mehr Einsichten führt.
- RMSE: Dieser ist besser als MSE, weil wir den Fehler in y interpretieren können.
Diese 3 sind nichts als die Verlustfunktionen.
# Bewertung des Modells
from sklearn import metrics
print('MAE:', metrics.mean_absolute_error(y_test, y_pred))
print('MSE:', metrics.mean_squared_error(y_test, y_pred))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
MAE: 3426.4269374307123
MSE: 21026037.329511296
RMSE: 4585.4157204675885
Fazit
Die lineare Regressionsanalyse ist ein leistungsstarkes Tool für Algorithmen zum maschinellen Lernen, mit dem sich kontinuierliche Variablen wie Gehalt, Umsatz, Leistung usw. vorhersagen lassen. Die lineare Regression berücksichtigt die lineare Beziehung zwischen unabhängigen und abhängigen Variablen. Einfache lineare Regression hat nur eine unabhängige Variable, auf deren Grundlage das Modell die Zielvariable vorhersagt. Wir haben das Modell und die Anwendung der linearen Regression anhand eines Beispiels für eine prädiktive Analyse zur Vorhersage des Gehalts von Mitarbeitern erörtert.
Empfohlene Artikel
Dies ist eine Anleitung zur einfachen linearen Regression. Hier diskutieren wir das Modell und die Anwendung der linearen Regression anhand eines Beispiels für eine prädiktive Analyse zur Vorhersage der Gehälter von Mitarbeitern. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren.
- Lineare Regressionsanalyse
- Lineare Regression in R
- Lineare Regressionsmodellierung
- Regressionstest-Tools
- Matplotlib In Python | Top 14 Grundstücke in Matplotlib
- Wörterbuch in Python | Methoden und Beispiele
- Beispiele für Square Root in PHP
- Lineare Regression vs Logistische Regression | Top Unterschiede