
Einführung in das Zinseszins-Beispiel
Es gibt zahlreiche Beispiele für Zinseszins. Das folgende Beispiel für Zinseszinsen gibt einen Überblick über die häufigsten Situationen, in denen Zinseszinsen berechnet werden und wie diese berechnet werden können. Da es mehrere Bereiche und Situationen gibt, in denen der Zinseszins berechnet werden kann, können nicht alle Arten von Beispielen angegeben werden. Im Folgenden werden einige Beispiele für Zinseszins aufgeführt, in denen die verschiedenen Situationen dargestellt sind
Beispiele für Zinseszins (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des Zinseszinses besser zu verstehen.
Sie können diese Excel-Beispielvorlage für Zinseszinsen hier herunterladen - Excel-Beispielvorlage für Zinseszinsen Im Folgenden finden Sie Beispiele für Zinseszinsen:Zinseszins Beispiel -1
Harry möchte die Ersparnisse aus dem von ihm verdienten Geld starten. Er beschließt dann, den anfänglichen Betrag von 10.000 USD auf das hochverzinsliche Sparkonto einzuzahlen. In diesem Fall beträgt der Zinssatz 15% pa und wird jährlich berechnet. Derzeit ist Harry 40 Jahre alt und plant, im Alter von 60 Jahren in den Ruhestand zu treten. Dies bedeutet, dass Harry einen Zeithorizont von 40 Jahren hat, über den er die Zinsen akkumulieren kann. Berechnen Sie den Geldbetrag, den Harry im Alter von 60 Jahren erhalten wird. Bereiten Sie außerdem die Tabelle vor, um die jährlichen Zinsen und den Kontowert anzuzeigen.
Gegeben,
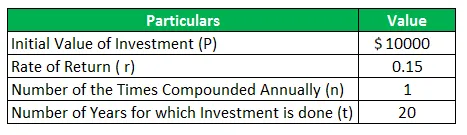
Lösung:
Unter Verwendung der angegebenen Informationen ergibt sich folgende Berechnung des Zinseszinses und des Betrags, der im Alter von 60 Jahren zu erhalten ist:
Die Berechnung des zukünftigen Investitionswerts unter Verwendung der Zinseszinsformel sieht wie folgt aus:
A = P (1 + r / n) nt

- A = $ 10.000 (1 + 0, 15 / 1) 1 * 20
- A = 10.000 USD (1 + 0, 15) 20
- A = 10.000 US-Dollar (1, 15) 20
- A = 10.000 USD * 16.367
- A = 163.665, 37 USD
Tabelle mit den jährlichen Zinsen und dem Kontowert
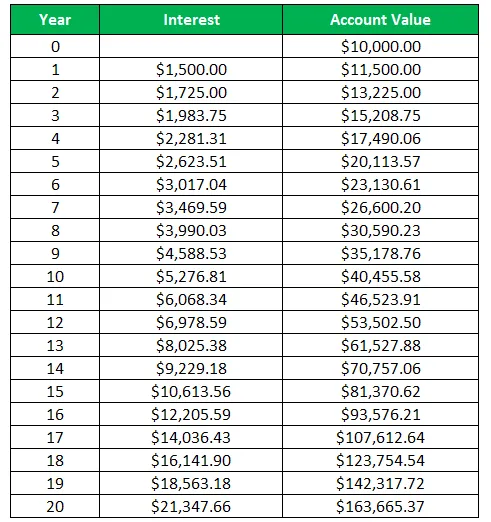
Hier wird das Interesse berechnet als:
- Zins = Anfangsinvestitionsbetrag * Zinssatz (r)
- Zins = 10000 * 15%
- Zinsen = 1500 USD
Ähnlich für alle Jahre.
und der Kontowert ist Berechnen als:
- Kontowert = ursprünglicher Investitionsbetrag + Zinsen
- Kontowert = 10000 + 1500
- Kontowert = $ 11500
Ähnlich für alle Jahre.
Im vorliegenden Beispiel sehen wir, dass der Kontowert der ursprünglich getätigten Investition in Höhe von 10.000 USD am Ende des Zeitraums von 20 Jahren 163.665, 37 USD beträgt. Dies unterstreicht die Stärke der Aufzinsung, da Harry mit Hilfe von Zinseszinsen sein Geld um ein Vielfaches vervielfachte, ohne die Investition aktiv zu verwalten. Hier konnte der Harry auch das Interesse an dem zuvor verdienten Interesse verdienen.
Zinseszins Beispiel -2
Sam tätigt eine Anfangsinvestition von 10.000 USD für einen Zeitraum von 5 Jahren. Er möchte wissen, welchen Investitionsbetrag er nach 5 Jahren erhält, wenn die Investition eine Rendite von 6% pa erzielt, die wöchentlich zusammengerechnet wird.
Gegeben,

Unter Zugrundelegung der angegebenen Informationen ergibt sich folgende Berechnung des Zinseszinses und des Betrags, der nach Ablauf von 5 Jahren zu erhalten ist:
Lösung:
Die Berechnung des zukünftigen Wertes einer Investition unter Verwendung der Zinseszinsformel sieht wie folgt aus:
A = P (1 + r / n) nt
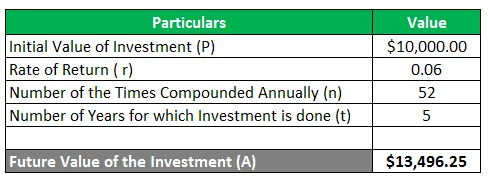
A = $ 10.000 (1 + 0, 6 / 52) 52 * 5
A = $ 10.000 (1 + 0, 00115) 260
A = $ 10.000 (1.00115) 260
A = 10.000 USD * 1.3496
A = 13.496, 25 USD
Im vorliegenden Beispiel sehen wir, dass der Kontowert der ursprünglich getätigten Investition in Höhe von 10.000 USD am Ende des Fünfjahreszeitraums, wenn die Aufzinsung wöchentlich erfolgt, 13.496, 25 USD beträgt. Die Aufzinsung erhöht den Wert der Investition am Ende des Zeitraums, da auch die zuvor verdienten Zinsen verzinst werden. Hier erfolgt die Compoundierung 52-mal, da es 52 Wochen im Jahr gibt.
Fazit - Zinseszinsbeispiel
Der Zinseszins ergibt im Vergleich zu einfachen Zinsen mehr Zinsen, da er sich aus der Aufladung von Zinsen auf den ausstehenden Kapitalbetrag ergibt, einschließlich Zinsen im Gegensatz zu einfachen Zinsen, bei denen Zinsen auf den ursprünglichen Kapitalbetrag erhoben werden und keine Zinsen über Zinsen erhoben werden. Die Kraft des Compoundierens hilft dabei, die Investition mit den Merkmalen der Exponentialfunktion schneller zu steigern. Dies ist das Ergebnis der Tatsache, dass sie trotz Amortisation der Investition wieder investiert werden, um schneller zu wachsen. Dies wird in der normalen Geschäftspraxis sehr häufig verwendet, sei es bei Darlehen oder Einlagen. Darüber hinaus wird die Häufigkeit der Compoundierung entscheidend für das Wachstum sein. Angenommen, wenn die Zinseszinshäufigkeit bei einem bestimmten Zinssatz pro Monat liegt, dann ist ihre annualisierte Rate höher als die der Zinseszinshäufigkeit halbjährlich oder jährlich.
Empfohlene Artikel
Dies war ein Leitfaden für das Zinseszinsbeispiel. Hier diskutieren wir, wie Zinseszinsen anhand ihrer Formel berechnet werden, zusammen mit praktischen Beispielen. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Tägliche Zinseszinsformel
- Beispiel für variable Kosten
- Quantitatives Forschungsbeispiel
- Monopolistische Wettbewerbsbeispiele
- Zins vs Dividende | Die acht wichtigsten Unterschiede, die Sie kennen sollten