
Einführung in die Fibonacci-Serie in Python
In der Fibonacci-Reihe in Python wird dies als eine Reihe von Zahlen bezeichnet, wobei die nächste Zahl die Summe der gegenwärtigen beiden Zahlen ist.
Beispielsweise:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Also hier 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 und so weiter.
Wenn man sich das oben anschaut, hätte man eine gewisse Vorstellung davon, wovon wir sprechen.
In Bezug auf die mathematische Regel kann es jedoch wie folgt geschrieben werden:

Dabei ist n-te Zahl die Summe der Zahlen an den Stellen (n-1) und (n-2). Wenn es um die Implementierung der Fibonacci-Reihe geht, könnte es eine Reihe von Codierungssprachen geben, mit denen dies möglich ist.
Python ist jedoch heutzutage eine weit verbreitete Sprache. Sehen wir uns die Implementierung der Fibonacci-Reihe durch Python an. Bevor Sie hier fortfahren, sollten Sie sich mit grundlegenden Bedingungsanweisungen wie der Schleife, if-else, while-Schleife usw. in Python vertraut machen. Wenn nicht, wäre es großartig, wenn man es überarbeiten und dann den kommenden Inhalt aufgreifen könnte. Hier für Demo-Zwecke verwende ich Spyder, die IDE für Python-Programmiersprache ist. Man kann auch andere IDE- oder Ipython-Notebooks für die Ausführung der Python-Programme verwenden.
Fibonacci-Serie in Python
Lassen Sie uns die Implementierung von Fibonacci-Zahl und -Serie unter Berücksichtigung der ersten beiden Elemente von Fibonacci, 0 und 1, betrachten:
Sie können jedoch die Funktion von Fibonacci nach Ihren Wünschen anpassen, aber zuerst die Grundlagen lesen und schrittweise zu anderen übergehen.
Python-Code zum Auffinden der n-ten Fibonacci-Zahl
Code 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Code 2:
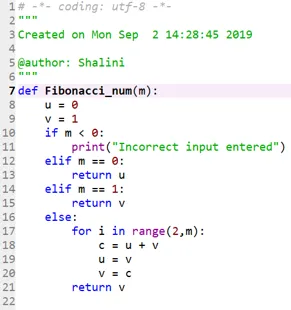
Ausgabe:
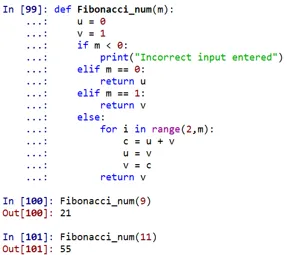
Wie man sehen kann, wäre die Fibonacci-Zahl auf dem 9. Platz 21 und auf dem 11. Platz 55.
- Hier ist "fibonacci_num" eine definierte Funktion, die sich mit Hilfe bestimmter Bedingungen darum kümmert, die Fibonacci-Zahl zu finden. Diese Funktion kann durch Angabe einer beliebigen Position aufgerufen werden.
Nun wollen wir sehen, wie man Serien bis zu der angegebenen Position drucken kann:
Code:
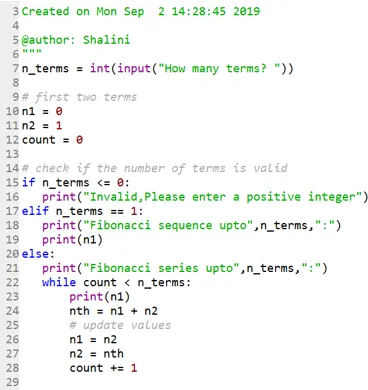
Ausgabe:
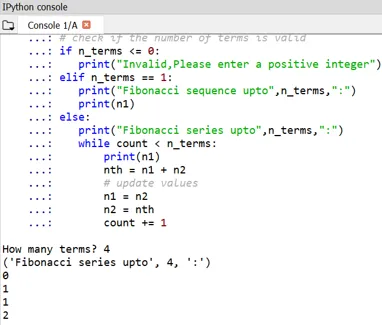
Man kann feststellen, dass der Beginn der Fibonacci-Zahlen als 0 und 1 definiert ist.
- Wenn jemand seine eigenen Startbegriffe definieren möchte, kann dies auch auf die gleiche Weise durch Ändern von n1 und n2 erfolgen. Hier ist das Beispiel dafür:
Nehmen wir jetzt an, wir wollen, dass unsere Startterme n1 = 3, n2 = 5 sind
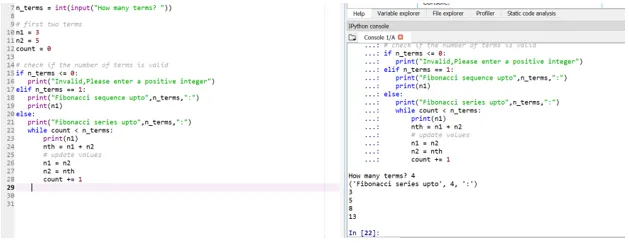
Hier wird also Ihre 4. Amtszeitposition (Benutzereingabe wird vorgenommen) basierend auf Ihren Startbedingungen festgelegt.
Methoden, mit denen Fibonacci-Reihen erzeugt werden können
Nachfolgend sind die drei Methoden aufgeführt, mit denen Fibonacci-Reihen generiert werden können:
1. Durch Generatoren
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Ausgabe:
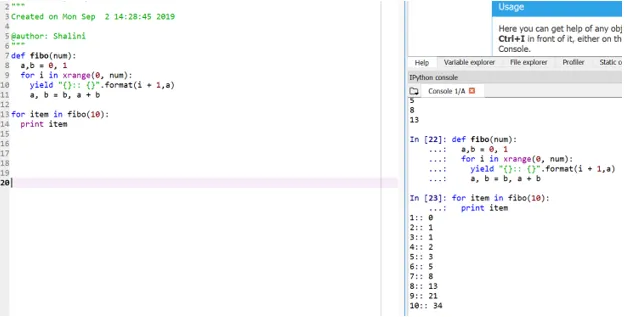
Diese Methode wird als "Generator" bezeichnet, da die Funktion xrange ein Generator für die Zahlen zwischen 0 und num ist und yield der Generator für die formatierte Ausgabe ist.
Das leistet xrange für Sie:

Hier wurde die Fibonacci-Reihe in Form einer Funktion definiert, in der sich die Funktion für Schleife, XRange und Yield um die Ausgabe kümmert.
2. Durch für Schleife
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Ausgabe:

Wie man sieht, wurde simple for loop verwendet, um die Fibonacci-Reihen zwischen 0 und 10 zu drucken. Innerhalb von for loop wurden den Variablen neue Werte zugewiesen. U und v sind die Standardanfangswerte von Fibonacci, die auf 0 bzw. 1 gesetzt wurden.
Wenn die Schleife ausgeführt wird, ist der neue u-Wert der alte v-Wert, während der neue v-Wert die Summe der alten Werte von u und v ist. Dies wird bis zum Ende der Bereichswerte fortgesetzt.
3. Durch Rekursion
Code:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Ausgabe:
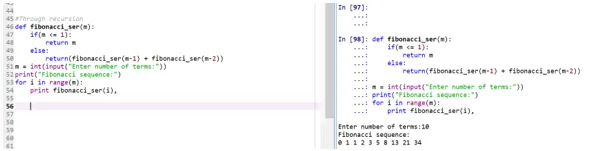
- Die Funktion „fibonacci_ser“ ruft sich auf, die Fibonacci-Reihe zu drucken.
- Und daher hat die Methode ihren Namen "Rekursion".
Schritte, die hier ausgeführt wurden:
- Hier wurde der Benutzer aufgefordert, den Ort einzugeben, bis zu dem die Fibonacci-Serie gedruckt werden soll.
- Nummer durchläuft die Funktion „fibonacci_ser“.
- Die Bedingung wird überprüft, ob die angegebene Länge kleiner als 1 ist oder nicht. Wenn ja, wird das Ergebnis sofort angezeigt.
- Ist die Länge jedoch größer als 1, werden rekursive Aufrufe an "fibonacci_ser" mit Argumenten mit einer Länge von weniger als 1 und 2, dh fibonacci_ser (m-1) und fibonacci_ser (m-2), durchgeführt.
- Die Rekursion liefert also die gewünschte Ausgabe und druckt sie aus.
- Kurz gesagt, wir haben drei Möglichkeiten für die Anzeige der Fibonacci-Reihe erörtert.
- Durch for-Schleife, durch Generatoren und durch Rekursion.
Alle drei Python-Codes zusammengefasst
Unten sind die drei Python-Code:
1. Durch Generatoren
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Durch für Schleife
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Durch Rekursion
Code:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Zusammengefasst sind alle Verfahren, die man üben muss, um alle in den Griff zu bekommen.
Ausgabe:
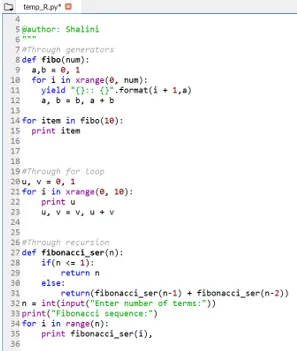
Fazit
Wenn man sich den obigen Inhalt von Fibonacci ansieht, hätte man kristallklares Verständnis für Fibonacci-Zahlen und -Serien, die auf Python spezialisiert sind. Wenn man sich einmal mit der Logik der Fibonacci-Reihe vertraut gemacht hat, wird das Erzeugen einer weiteren Reihe von Reihen, das Arbeiten mit anderen Zahlen und mit verschiedenen Methoden zu einem Kinderspiel. Ein logischer Ansatz ist der einzige Weg, um dies zu übertreffen.
Empfohlene Artikel
Dies ist eine Anleitung zur Fibonacci-Serie in Python. Hier besprechen wir Fibonacci-Zahlen und -Serien, die auf Python spezialisiert sind und einen weiteren Satz von Reihen erzeugen, die mit anderen Zahlen und mit verschiedenen Methoden arbeiten. Sie können auch unsere anderen verwandten Artikel durchgehen, um mehr zu erfahren -
- Zufallszahlengenerator in Python
- Mathematische Funktionen in Python
- Fakultät in Python
- Kapselung in Python
- Fibonacci-Reihe in Java
- Python-Funktionen
- Factorial-Programm in JavaScript
- Zufallszahlengenerator in Matlab
- Zufallszahlengenerator in C #
- Kapselung in JavaScript