
Einführung in die Binomialverteilung in R
Dieser Artikel beschreibt, wie Binomialverteilungen in R für die wenigen Operationen verwendet werden, die mit Wahrscheinlichkeitsverteilungen zu tun haben. Business Analysis nutzt die Binomialwahrscheinlichkeit für ein komplexes Problem. R verfügt über zahlreiche integrierte Funktionen zur Berechnung von Binomialverteilungen, die bei statistischen Interferenzen verwendet werden. Die Binomialverteilung, auch Bernoulli-Versuche genannt, unterscheidet zwei Arten von Erfolg p und Misserfolg S. Das Hauptziel des Binomialverteilungsmodells besteht darin, die möglichen Wahrscheinlichkeitsergebnisse zu berechnen, indem eine bestimmte Anzahl positiver Möglichkeiten überwacht wird, indem der Prozess eine bestimmte Anzahl von Malen wiederholt wird . Sie sollten zwei mögliche Ergebnisse haben (Erfolg / Misserfolg), daher ist das Ergebnis dichotom. Die vordefinierte mathematische Notation lautet p = Erfolg, q = 1-p.
Es gibt vier Funktionen, die Binomialverteilungen zugeordnet sind. Sie sind dbinom, pbinom, qbinom, rbinom. Die formatierte Syntax ist unten angegeben:
Syntax
- dbinom (x, größe, prob)
- pbinom (x, size, prob)
- qbinom (x, size, prob) oder qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, size, prob)
Die Funktion hat drei Argumente: Der Wert x ist ein Vektor von Quantilen (von 0 bis n), die Größe ist die Anzahl der Trails-Versuche, prob gibt die Wahrscheinlichkeit für jeden Versuch an. Lassen Sie uns eins nach dem anderen mit einem Beispiel sehen.
1) dbinom ()
Es ist eine Dichte- oder Verteilungsfunktion. Die Vektorwerte müssen eine ganze Zahl sein und dürfen keine negative Zahl sein. Diese Funktion versucht, eine Reihe von Erfolgen in einer Nr. Zu finden. von Versuchen, die behoben sind.
Eine Binomialverteilung nimmt Größen- und x-Werte an. Beispiel: size = 6, die möglichen x-Werte sind 0, 1, 2, 3, 4, 5, 6, was P (X = x) impliziert.
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Ausgabe:
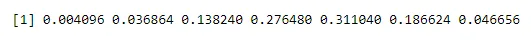
Wahrscheinlichkeit eins machen
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Ausgabe:
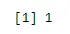
Beispiel 1 - Die Krankenhausdatenbank zeigt, dass 65% der an Krebs erkrankten Patienten daran sterben. Wie groß ist die Wahrscheinlichkeit, dass sich 5 zufällig ausgewählte Patienten, von denen sich 3 erholen, erholen?
Hier wenden wir die dbinom Funktion an. Die Wahrscheinlichkeit, dass sich 3 bei Verwendung der Dichteverteilung an allen Punkten erholt.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Ausgabe:

Für x Wert 0 bis 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Ausgabe:
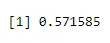
Erstellen Sie als Nächstes ein Beispiel aus 40 Papieren und erhöhen Sie es mit dbinom um 2, um ebenfalls ein Binomial zu erstellen.
a <- seq(0, 40, by = 2)
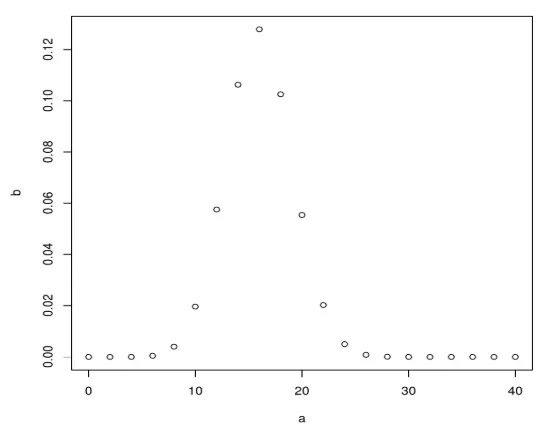
b <- dbinom(a, 40, 0.4)
plot(a, b)
Nach Ausführung des obigen Codes wird die folgende Ausgabe erzeugt. Die Binomialverteilung wird mit der Funktion plot () gezeichnet.
Beispiel 2 - Stellen Sie sich ein Szenario vor. Nehmen wir an, dass die Wahrscheinlichkeit, dass ein Schüler ein Buch aus einer Bibliothek ausleiht, 0, 7 beträgt. Die Bibliothek besteht aus 6 Studenten. Wie hoch ist die Wahrscheinlichkeit, dass 3 von ihnen ein Buch ausleihen?
hier P (X = 3)
Code:
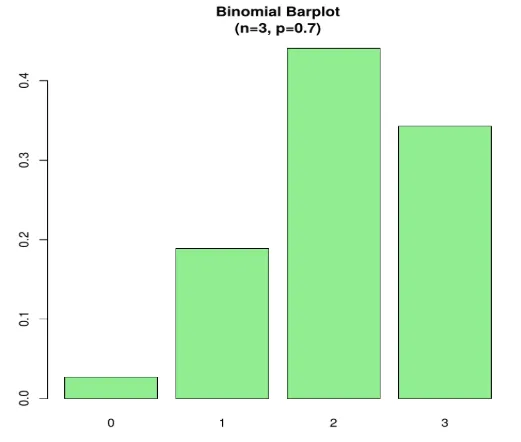
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Unterhalb des Diagramms wird angezeigt, wenn p> 0, 5, daher ist die Binomialverteilung wie angezeigt positiv verzerrt.
Ausgabe:
2) Pbinom ()
berechnet kumulative Wahrscheinlichkeiten von Binomial oder CDF (P (X <= x)).
Beispiel 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Ausgabe:

Beispiel 2: Dravid erzielt bei 20% seiner Versuche ein Tor, wenn er bowlt. Wenn er fünfmal bowlt, wie hoch ist die Wahrscheinlichkeit, dass er vier oder weniger Pforten erzielt?
Die Erfolgswahrscheinlichkeit beträgt hier 0, 2 und bei 5 Versuchen erhalten wir
pbinom(4, size=5, prob=.2)
Ausgabe:
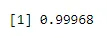
Beispiel 3: 4% der Amerikaner sind schwarz. Bestimmen Sie die Wahrscheinlichkeit von 2 schwarzen Schülern, wenn Sie zufällig 6 Schüler aus einer Klasse von 100 ohne Ersatz auswählen.
Wenn R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Ausgabe:-
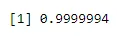
3) qbinom ()
Es ist eine Quantilfunktion und führt die Umkehrung der kumulativen Wahrscheinlichkeitsfunktion durch. Der kumulative Wert stimmt mit einem Wahrscheinlichkeitswert überein.
Beispiel: Wie viele Schwänze haben eine Wahrscheinlichkeit von 0, 2, wenn eine Münze 61 Mal geworfen wird.
a <- qbinom(0.2, 61, 1/2)
print(a)
Ausgabe:-
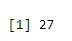
4) rbinom ()
Es werden Zufallszahlen generiert. Unterschiedliche Ergebnisse erzeugen unterschiedliche Zufallsausgaben, die im Simulationsprozess verwendet werden.
Beispiel:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Ausgabe:-

Jedes Mal, wenn wir es ausführen, gibt es zufällige Ergebnisse.
rbinom(200, 4, 0.4)
Ausgabe:-

Hier setzen wir das Ergebnis von 30 Münzwürfen in einem einzigen Versuch voraus.
rbinom(30, 1, 0.5)
Ausgabe:-
Barplot verwenden:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Ausgabe:-
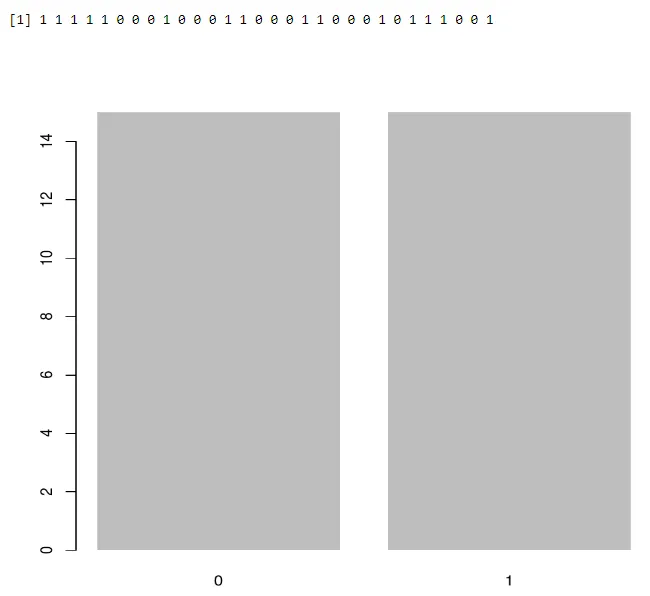
Das Mittel des Erfolgs finden
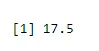
output <-rbinom(10, size=60, 0.3)
mean(output)
Ausgabe:-
Schlussfolgerung - Binomialverteilung in R
Daher haben wir in diesem Dokument die Binomialverteilung in R erörtert. Wir haben verschiedene Beispiele in R studio und R snippets simuliert und auch die eingebauten Funktionen beschrieben, die bei der Erzeugung von Binomialberechnungen hilfreich sind. Die Binomialverteilungsberechnung in R verwendet statistische Berechnungen. Daher hilft eine Binomialverteilung beim Finden der Wahrscheinlichkeit und der Zufallssuche unter Verwendung einer Binomialvariablen.
Empfohlene Artikel
Dies ist ein Leitfaden zur Binomialverteilung in R. Hier haben wir eine Einführung und die mit der Binomialverteilung verbundenen Funktionen zusammen mit der Syntax und den entsprechenden Beispielen besprochen. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren -
- Binomialverteilungsformel
- Wirtschaft vs Business
- Business Analytics-Techniken
- Linux-Distributionen