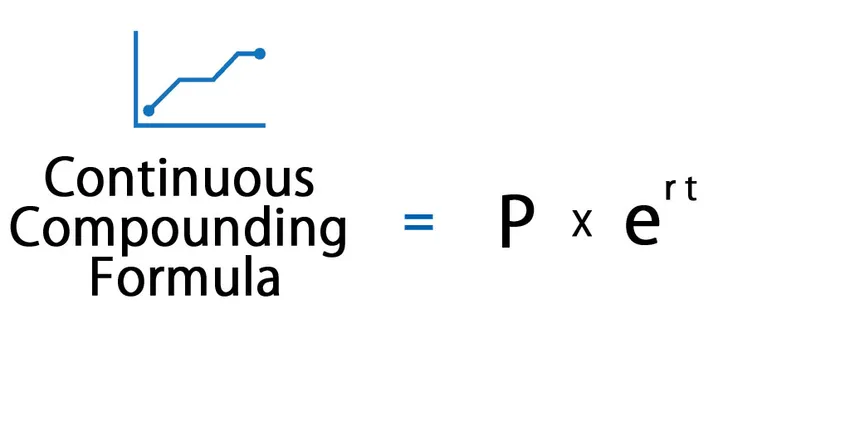
Kontinuierliche Mischformel

Kontinuierliche Mischformel (Inhaltsverzeichnis)

Kontinuierliche Mischformel
Kontinuierlicher Compounding-Rechner
Fortlaufende zusammengesetzte Formel in Excel (mit Excel-Vorlage)

Bevor wir zum kontinuierlichen Zinseszinskonzept übergehen, sollten wir zunächst verstehen, was Zinseszins ist. Zinseszins bedeutet, dass die Zinsen, die Anleger jedes Jahr verdienen, zu ihrem Kapital hinzugerechnet werden, sodass der Betrag nicht nur wächst, sondern auch schneller wächst als der einfache Zinssatz - dies ist eines der nützlichsten Konzepte im Finanzbereich. Es ist die Basis für alles, vom langfristigen Anlageplan auf dem Aktienmarkt bis zum persönlichen Sparplan. Sie berücksichtigt auch die Auswirkungen der Inflation auf den Betrag und die Bedeutung der Bezahlung der Schulden Rechner (Excel-Vorlage).

Für eine kontinuierliche Zinserhöhung wird der Zinssatz in jedem Moment hinzugefügt. Dies macht die Berechnung schwierig. Dies wird von keinem Finanzinstitut für Zinsaufwendungen verwendet, da es kaum Unterschiede zwischen dem kontinuierlichen Aufzinsungsbetrag und dem täglichen Aufzinsungsbetrag gibt. Banken verwenden für einige ihrer Produkte den täglichen Zinseszinsbetrag.

Die Formel für die kontinuierliche Compoundierung lautet wie folgt:

Die Formel für die fortlaufende Verzinsung berechnet die Zinsen, die für einen unendlichen Zeitraum fortlaufend verzinst werden.

wo,

P = Kapitalbetrag (Barwert des Betrags)

t = Zeit (Zeit ist Jahre)

r = Zinssatz.

Die obige Berechnung geht von einem konstanten Zinseszins über einen unendlichen Zeitraum aus. Da der genannte Zeitraum unendlich ist, hilft die Exponentenfunktion (e) bei der Multiplikation des aktuellen Investitionsbetrags. Dies wird mit dem aktuellen Zinssatz und Zeitraum multipliziert. Trotz einer großen Anzahl von Investitionen ist die Differenz zwischen den Gesamtzinsen, die durch kontinuierliche Aufzinsung in Excel erzielt werden, dieselbe wie bei herkömmlichen Aufzinsungen.

Beispiele und Erklärung der kontinuierlichen Mischformel

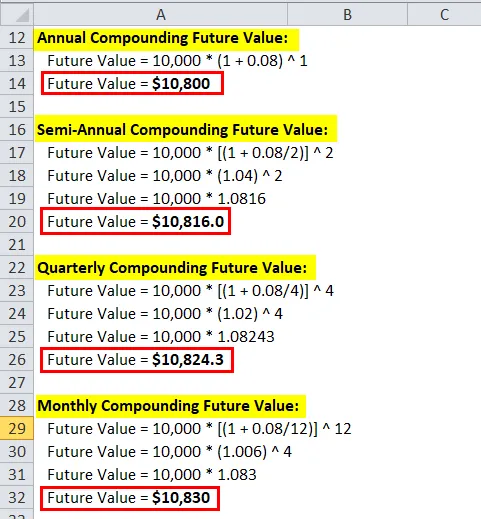
Berechnen Sie den Zinseszins auf 10.000 USD mit einem Zinssatz von 8% und einem Zeitraum von 1 Jahr. Die Aufzinsungshäufigkeit beträgt ein Jahr, halbjährlich, vierteljährlich, monatlich und kontinuierlich.

Sie können diese Endlosschablone hier herunterladen - Endlosschablone

Jährlicher zusammengesetzter zukünftiger Wert:

Zukünftiger Wert = 10.000 * (1 + 0, 08) 1
Zukünftiger Wert = 10.800 USD

Halbjahres-Zinseszins-Future-Wert:

Zukünftiger Wert = 10.000 * ((1 + 0, 08 / 2)) 2
Zukünftiger Wert = 10.000 * (1, 04) 2
Zukünftiger Wert = 10.000 * 1.0816
Zukünftiger Wert = 10.816, 0 USD

Vierteljährlicher zusammengesetzter zukünftiger Wert:

Zukünftiger Wert = 10.000 * ((1 + 0, 08 / 4)) 4
Zukünftiger Wert = 10.000 * (1, 02) 4
Zukünftiger Wert = 10.000 * 1.08243
Zukünftiger Wert = 10.824, 3 USD

Monatlicher zukünftiger Aufzinsungswert:

Zukünftiger Wert = 10.000 * ((1 + 0, 08 / 12)) 12
Zukünftiger Wert = 10.000 * (1.006) 4
Zukünftiger Wert = 10.000 * 1.083
Zukünftiger Wert = 10.830 USD

Continuous Compounding Future Value:

Zukünftiger Wert = 10.000 * e ^{0, 08}
Zukünftiger Wert = 10.000 * 1.08328
Zukünftiger Wert = 10.832, 87 USD

Wie aus dem obigen Beispiel für Berechnungen von Compoundierungen mit unterschiedlichen Häufigkeiten ersichtlich ist, beträgt der aus der kontinuierlichen Compoundierung berechnete Zins 832, 9 USD, was nur 2, 9 USD mehr ist als die monatliche Compoundierung. Es ist also der Fall, dass im praktischen Leben ein monatlicher oder ein täglicher Zinseszins als ein kontinuierlicher Zinseszins verwendet wird.

Bedeutung und Verwendung der kontinuierlichen Mischformel

Die Bedeutung der kontinuierlichen Mischformel ist:

Anstatt die Zinsen jährlich, vierteljährlich oder monatlich fortlaufend zu verzinsen, wird Continuous Compounding Excel Gewinne effizient und dauerhaft reinvestieren.
Der kontinuierliche Aufzinsungseffekt ermöglicht, dass die kontinuierliche Aufzinsung des Zinsbetrags zum gleichen Zinssatz reinvestiert wird, wodurch ein Anleger die Möglichkeit erhält, Renditen mit einem exponentiellen Zinssatz zu erzielen.
Die fortlaufende Aufzinsung bestimmt, dass nicht nur der Kapitalbetrag, sondern auch die fortlaufende Aufzinsung des Zinsbetrags den Betrag weiter multipliziert.

Die Aufzinsung kann jährlich, halbjährlich, vierteljährlich, täglich oder kontinuierlich erfolgen. Der Unterschied zwischen diesen Zeiträumen besteht darin, dass nach Ablauf des Zeitraums alle Zinsen, die verdient werden, als neuer Kapitalgeber behandelt werden. Wenn zum Beispiel die Zinseszinsrate halbjährlich ist, werden die Zinsen nach sechs Monaten zum Kapital hinzugerechnet. Dieser Zyklus dauert bis zur Fälligkeit an. Gleiches gilt für einen anderen Zeitraum: Die jährlichen Zinsen werden nach einem Jahr, die vierteljährlichen Zinsen nach drei Monaten und die täglichen Zinsen am nächsten Tag hinzugerechnet.

Kontinuierlicher Compounding-Rechner

Sie können den folgenden fortlaufenden Compounding-Rechner verwenden

P
r
t
Kontinuierliche Mischformel =

Kontinuierliche Mischformel =	P xe ^(rxt)
=	0 xe ^{(0 x 0)} = 0

Fortlaufende zusammengesetzte Formel in Excel (mit Excel-Vorlage)

Hier werden wir das gleiche Beispiel für die Continuous Compounding-Formel in Excel machen. Es ist sehr einfach und unkompliziert. Sie müssen die drei Eingaben eingeben, dh Kapitalbetrag, Zinssatz und Zeit.

Sie können die kontinuierliche Compoundierung mithilfe der Formel in der bereitgestellten Vorlage leicht berechnen.

Zuerst müssen wir den Betrag der kontinuierlichen Aufzinsung mit der Formel berechnen

dann müssen wir die Auswirkungen derselben auf die reguläre Compoundierung berechnen:

Empfohlene Artikel

Dies war ein Leitfaden für eine Formel zur kontinuierlichen Compoundierung. Hier diskutieren wir seine Verwendung zusammen mit praktischen Beispielen. Wir stellen Ihnen auch den Continuous Compounding Calculator mit einer herunterladbaren Excel-Vorlage zur Verfügung. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -

Tax Credit vs Tax Deduction - Vergleich
Unterschied zwischen einfachem Zinssatz und Zinseszins
Diskontsatz vs Zinssatz - Top Unterschiede
Top-Techniken für beste Online-Verkäufe

Kontinuierliche Mischformel - Rechner (Excel-Vorlage)

Inhaltsverzeichnis: