
Formel für die durchschnittliche jährliche Wachstumsrate (Inhaltsverzeichnis)
- Formel
- Beispiele
- Taschenrechner
Was ist die Formel für die durchschnittliche jährliche Wachstumsrate?
Aufzinsung ist der Effekt, bei dem eine Investition nicht nur eine Verzinsung der Hauptkomponente, sondern auch eine Verzinsung der Zinsen erzielt. Die durchschnittliche jährliche Wachstumsrate ist also das effektive jährliche Wachstum, das durch Investitionen erzielt wird. Dies setzt grundsätzlich voraus, dass die jährlich verdienten Zinsen reinvestiert werden und die gleichen Zinsen wie der Nennbetrag erzielt werden. Aus diesem Grund ist die durchschnittliche jährliche Wachstumsrate immer höher als der einfache Zinssatz. Viele Anlagen wie Investmentfonds und Börsenrenditen sind nicht sehr linear und sehr instabil.
Die durchschnittliche jährliche Wachstumsrate hilft dabei, diese Rendite auszugleichen, und gibt Auskunft darüber, wie viel ein Anleger über die Laufzeit der Anlage verdient hat, da alle Erträge zwischen diesem Zeitraum zum gleichen Zinssatz reinvestiert werden. Aufgrund dieses Glättungseffekts können wir Datensätze mit unterschiedlicher Volatilität vergleichen. Es wird sehr häufig für Zwecke der Finanzanalyse verwendet.
Anlageendbetrag = Startbetrag (1 + CAGR) Anzahl der Jahre
Die Formel für die durchschnittliche jährliche Wachstumsrate -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Diese Formel ist anwendbar, wenn die Investition jährlich zusammengesetzt wird, was bedeutet, dass wir das Geld jährlich reinvestieren. Manchmal kommt es jedoch vor, dass wir die Rate berechnen möchten, mit der die Aufzinsung vierteljährlich, monatlich und täglich erfolgt. Dazu verwenden wir die folgende Formel:
Anlageendbetrag = Startbetrag (1 + CAGR / Zinseszins) (Anzahl der Jahre * Zinseszins)
Also, eine Formel für Compounded Annual Growth Rate -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Mischfrequenz:
- Halbjährliche Aufzinsung: 2
- Vierteljährliche Aufzinsung: 4
- Monatshäufigkeit: 12 und so weiter
Beispiele für CAGR-Formeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung der CAGR-Formel besser zu verstehen.
Sie können diese Excel-Vorlage für die berechnete jährliche Wachstumsrate hier herunterladen - Excel-Vorlage für die berechnete jährliche WachstumsrateCAGR-Formel - Beispiel # 1
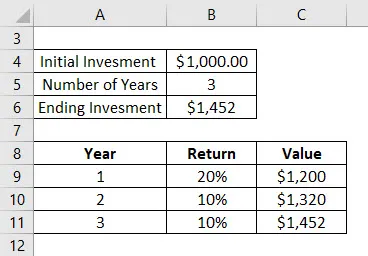
Angenommen, Sie haben vor 3 Jahren 1000 USD in Investmentfonds investiert. Das Folgende ist die Rendite, die Sie für diese 3 Jahre haben:
- Im ersten Jahr haben Sie eine Wertsteigerung von 20%. Der Gesamtwert beträgt also am Ende des ersten Jahres 1200 US-Dollar
- 2. Jahr, Sie haben eine 10% ige Wertsteigerung. Der Gesamtwert beträgt also am Ende des 2. Jahres 1320 USD
- 3. Jahr, Sie haben eine 10% ige Wertsteigerung. Der Gesamtwert beträgt also am Ende des dritten Jahres 1452 USD
Die CAGR wird nach der unten angegebenen Formel berechnet
CAGR = (Ending Investment Amount / Start Amount) (1 / Anzahl der Jahre) - 1
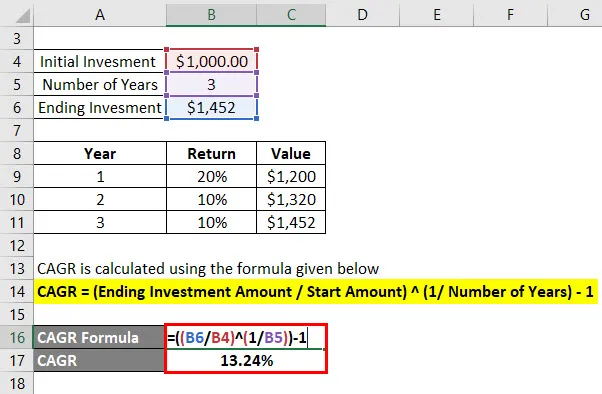
- CAGR = (1.452 $ / 1.000 $) (1/3) - 1
- CAGR = 13, 24%
Hier können wir sehen, dass die jährliche Rendite für alle drei Jahre unterschiedlich ist und variiert, aber die zusammengesetzte jährliche Wachstumsrate gibt uns eine einzige Rate, die wir mit verschiedenen Investitionsmöglichkeiten vergleichen können.
CAGR-Formel - Beispiel # 2
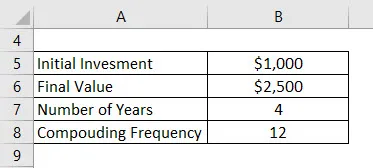
Nehmen wir an, Sie haben 1000 USD in die Bank investiert und möchten das Geld für 4 Jahre in der Bank behalten. Angenommen, Sie erhalten nach 4 Jahren einen Gesamtbetrag von 2500 USD. Eine Bank bietet einen Zinssatz mit monatlicher Aufzinsung an. CAGR berechnen.
Die CAGR wird nach der unten angegebenen Formel berechnet
CAGR = Zinseszinshäufigkeit * ((Endanlagebetrag / Startbetrag) (1 / (Anzahl der Jahre * Zinseszinshäufigkeit)) - 1)
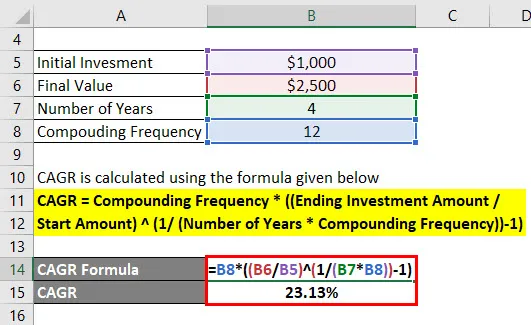
- CAGR = 12 * (($ 2.500 / $ 1.000) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Die durchschnittliche jährliche Wachstumsrate beträgt 23, 13%.
Erklärung der Formel für die durchschnittliche jährliche Wachstumsrate
Obwohl die durchschnittliche jährliche Wachstumsrate die jährliche Rate für die Investition ist, ist sie nur eine theoretische Zahl und nicht die wahre Rendite. Die Hauptannahme hierbei ist, dass alle Erträge für den Anlagezeitraum zum gleichen Zinssatz reinvestiert werden, der Zinssatz jedoch nicht für alle Jahre erhalten bleibt und wir unser Geld möglicherweise nicht zum gleichen Zinssatz anlegen. Es ist also ein einzig repräsentativer Kurs, der uns sagt, was wir möglicherweise erreichen, wenn das gesamte Geld am Ende eines jeden Jahres zu diesem Kurs reinvestiert wird. Es gibt also einige wichtige Punkte, die wir berücksichtigen sollten, wenn wir die durchschnittliche jährliche Wachstumsrate verwenden.
Wir werden auch sehr vorsichtig mit einer Investition sein, die sich über einen langen Zeitraum erstreckt. Wenn zum Beispiel eine Investitionsperiode sehr lang ist, zum Beispiel 20 Jahre, kann der Zinseszins einen falschen Hinweis liefern, da wir in den ersten 15 Jahren möglicherweise keine Gewinne erzielen und alle Renditen in der letzten Periode erzielt werden . 15 Jahre lang keine Gewinne zu erzielen, ist für kein Unternehmen akzeptabel.
Wenn zwei Anlagemöglichkeiten den gleichen CAGR aufweisen, kann dies auch der Fall sein, dass die eine Anziehungskraft auf die andere zunimmt, da sich das Wachstum in der einen Phase in der Anfangsphase abspielt und in der anderen Phase am Ende des Jahres konzentriert Zeitraum.
Relevanz und Verwendung der Formel für die durchschnittliche jährliche Wachstumsrate
Die durchschnittliche jährliche Wachstumsrate ist sehr hilfreich bei der Berechnung der durchschnittlichen Wachstumsrate der Anlage und kann beim Vergleich verschiedener Anlagen hilfreich sein. Wie wir im obigen Beispiel gesehen haben, ist das jährliche Wachstum der Investitionen ungleichmäßig und unregelmäßig. Bei Verwendung der jährlichen Wachstumsrate glättet sich die Rendite jedoch. Ein weiterer Faktor, der die durchschnittliche jährliche Wachstumsrate zu einer entscheidenden Methode zur Bestimmung des Wachstums einer Investition macht, ist die Berücksichtigung des Zinseszinseffekts, der bei der jährlichen Rendite nicht berücksichtigt wird. Der berechnete Jahreszins gibt uns kein tatsächliches Bild der Rendite, da er nur die Rendite des Kapitalbetrags berechnet und die Zinskomponente ignoriert. Dies ist jedoch bei der berechneten jährlichen Wachstumsrate nicht der Fall.
Formelrechner für die durchschnittliche jährliche Wachstumsrate
Sie können den folgenden Compounded Annual Growth Rate Calculator verwenden
| Endbetrag der Investition | |
| Startbetrag | |
| Anzahl der Jahre | |
| CAGR | |
| CAGR = | ((Ending Investment Amount / Start Amount) 1 / Anzahl der Jahre -1) |
| = | ((0/0) 1/0 -1) = 0 |
Empfohlene Artikel
Dies war ein Leitfaden für die Formel für die durchschnittliche jährliche Wachstumsrate. Hier diskutieren wir die Berechnung der CAGR anhand praktischer Beispiele. Wir bieten auch einen Compounded Annual Growth Rate-Rechner mit einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Leitfaden für die Renditeformel
- Beispiele für Exponential Growth Formula
- Rechner für die zentrale Grenzwertsatzformel
- Wie berechnet man die Marktkapitalisierung?