
Rand der Fehlerformel (Inhaltsverzeichnis)
- Margin of Error Formula
- Beispiele für die Margin of Error-Formel (mit Excel-Vorlage)
- Margin of Error Formula Calculator
Margin of Error Formula
In der Statistik berechnen wir das Konfidenzintervall, um zu sehen, wo der Wert der Daten der Stichprobenstatistik abfällt. Der Wertebereich, der in einem Konfidenzintervall unterhalb und oberhalb der Stichprobenstatistik liegt, wird als Fehlergrenze bezeichnet. Mit anderen Worten, es ist im Grunde der Fehlergrad in der Stichprobenstatistik. Je höher die Fehlerquote, desto geringer ist das Vertrauen in die Ergebnisse, da der Grad der Abweichung von diesen Ergebnissen sehr hoch ist. Wie der Name schon sagt, liegt die Fehlerquote in einem Bereich von Werten über und unter den tatsächlichen Ergebnissen. Wenn wir zum Beispiel in einer Umfrage eine Antwort erhalten, in der 70% der Befragten „gut“ geantwortet haben und die Fehlerquote 5% beträgt, bedeutet dies, dass 65% bis 75% der Bevölkerung die Antwort „gut“ finden. .
Die Formel für die Fehlergrenze -
Margin of Error = Z * S / √n
Wo:
- Z- Z-Score
- S - Standardabweichung einer Population
- n - Stichprobengröße
Eine andere Formel zur Berechnung der Fehlerquote lautet:
Margin of Error = Z * √((p * (1 – p)) / n)
Wo:
- p - Probenanteil (Anteil der Probe, der ein Erfolg ist)
Um nun den gewünschten Z-Score zu finden, müssen Sie das Konfidenzintervall der Stichprobe kennen, da der Z-Score davon abhängig ist. Die folgende Tabelle zeigt die Beziehung zwischen Konfidenzintervall und z-Punktzahl:
| Konfidenzintervall | Z - Score |
| 80% | 1.28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Sobald Sie das Konfidenzintervall kennen, können Sie den entsprechenden z-Wert verwenden und daraus die Fehlertoleranz berechnen.
Beispiele für die Margin of Error-Formel (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung der Fehlergrenze besser zu verstehen.
Sie können diese Margin of Error-Vorlage hier herunterladen - Margin of Error-VorlageRand der Fehlerformel - Beispiel # 1
Nehmen wir an, wir führen eine Umfrage durch, um herauszufinden, welche Noten die Studenten bekommen. Wir haben 500 Schüler nach dem Zufallsprinzip ausgewählt und nach ihrer Punktzahl gefragt. Der Durchschnitt liegt bei 2, 4 von 4 und die Standardabweichung bei 30%. Angenommen, das Konfidenzintervall beträgt 99%. Berechnen Sie die Fehlerquote.
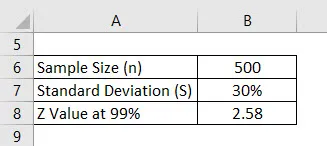
Lösung:
Die Fehlerquote wird nach der unten angegebenen Formel berechnet
Fehlergrenze = Z * S / √n
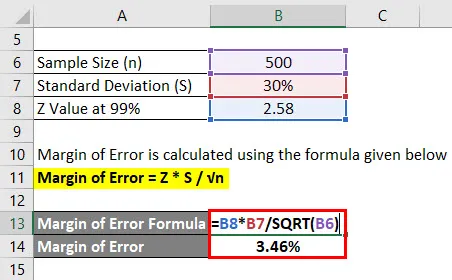
- Fehlerquote = 2, 58 * 30% / √ (500)
- Fehlerquote = 3, 46%
Dies bedeutet, dass bei einer Zuverlässigkeit von 99% die Durchschnittsnote der Schüler 2, 4 plus oder minus 3, 46% beträgt.
Rand der Fehlerformel - Beispiel # 2
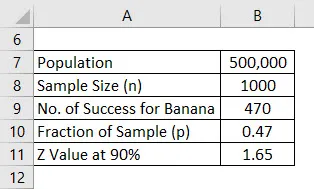
Nehmen wir an, Sie bringen ein neues Gesundheitsprodukt auf den Markt, sind aber verwirrt, welchen Geschmack die Leute mögen. Sie sind verwirrt zwischen Bananengeschmack und Vanillegeschmack und haben sich für eine Umfrage entschieden. Ihre Bevölkerung dafür ist 500.000, was Ihr Zielmarkt ist, und aus diesem Grund haben Sie beschlossen, die Meinung von 1000 Personen einzuholen, und das wird die Stichprobe sein. Angenommen, ein Konfidenzintervall beträgt 90%. Berechnen Sie die Fehlerquote.
Lösung:
Nach Abschluss der Umfrage erfuhren Sie, dass 470 Personen das Bananenaroma mochten und 530 nach Vanillearoma fragten.
Die Fehlerquote wird nach der unten angegebenen Formel berechnet
Fehlergrenze = Z * √ ((p * (1 - p)) / n)
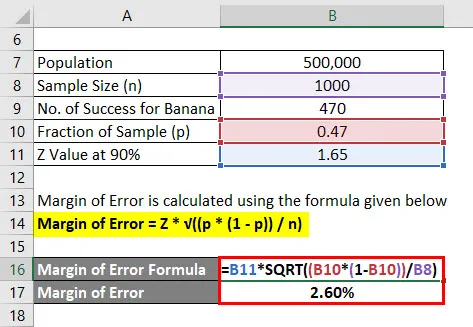
- Fehlergrenze = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Fehlerquote = 2, 60%
Wir können also mit 90% Selbstvertrauen sagen, dass 47% aller Menschen Bananengeschmack plus oder minus 2, 60% mochten.
Erläuterung
Wie oben erläutert, hilft uns die Fehlerquote zu verstehen, ob der Stichprobenumfang Ihrer Umfrage angemessen ist oder nicht. Falls der Randfehler zu groß ist, kann es sein, dass unsere Stichprobengröße zu klein ist und wir diese erhöhen müssen, damit die Stichprobenergebnisse besser mit den Populationsergebnissen übereinstimmen.
Es gibt einige Szenarien, in denen die Fehlerspanne keine große Rolle spielt und uns bei der Verfolgung des Fehlers nicht hilft:
- Wenn die Fragen der Umfrage nicht ausgelegt sind und nicht dazu beitragen, die erforderliche Antwort zu erhalten
- Wenn die Personen, die an der Umfrage teilnehmen, Vorurteile in Bezug auf das Produkt haben, für das die Umfrage durchgeführt wird, ist das Ergebnis ebenfalls nicht sehr genau
- Wenn die ausgewählte Stichprobe selbst der richtige Vertreter der Bevölkerung ist, sind die Ergebnisse auch in diesem Fall weit entfernt.
Auch hier ist eine große Annahme, dass die Bevölkerung normal verteilt ist. Wenn also die Stichprobengröße zu klein ist und die Populationsverteilung nicht normal ist, kann der z-Score nicht berechnet werden und wir können die Fehlergrenze nicht finden.
Relevanz und Verwendung der Margin of Error-Formel
Wann immer wir Beispieldaten verwenden, um eine relevante Antwort für die Grundgesamtheit zu finden, gibt es einige Unsicherheiten und Chancen, dass das Ergebnis vom tatsächlichen Ergebnis abweichen kann. Anhand der Fehlerspanne können wir erkennen, dass es sich bei der Abweichung um die Ausgabe der Stichprobe handelt. Wir müssen die Fehlerquote minimieren, damit unsere Stichprobenergebnisse den tatsächlichen Verlauf der Populationsdaten abbilden. Verringern Sie also die Fehlerquote, umso besser sind die Ergebnisse. Die Fehlerquote ergänzt und vervollständigt die uns vorliegenden statistischen Informationen. Wenn zum Beispiel eine Umfrage ergibt, dass 48% der Menschen es vorziehen, am Wochenende zu Hause zu sein, können wir nicht so genau sein und es fehlen einige Elemente in diesen Informationen. Wenn wir hier eine Fehlerquote von beispielsweise 5% eingeführt haben, wird das Ergebnis so interpretiert, dass 43-53% die Idee, am Wochenende zu Hause zu sein, mochten, was durchaus Sinn macht.
Margin of Error Formula Calculator
Sie können den folgenden Margin of Error-Rechner verwenden
| Z | |
| S | |
| √n | |
| Fehlermarge | |
| Fehlermarge | = |
|
|
Empfohlene Artikel
Dies war ein Leitfaden für die Margin of Error-Formel. Hier diskutieren wir, wie die Margin of Error mit praktischen Beispielen berechnet wird. Wir bieten auch einen Margin of Error-Rechner mit herunterladbarer Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Leitfaden zur linearen Abschreibungsformel
- Beispiele für die Verdopplungszeitformel
- Wie berechnet man die Amortisation?
- Formel für den zentralen Grenzwertsatz
- Altman Z Score | Definition | Beispiele
- Abschreibungsformel | Beispiele mit Excel-Vorlage