
Was ist Bootstrapping?
Der Begriff Bootstrapping bezieht sich auf die Methode, eine Nullkupon-Renditekurve aus den Marktpreisen eines Satzes kuponauszahlender Anleihen zu erstellen. Die Bootstrapping-Technik wird hauptsächlich verwendet, um die Rendite der Schatzwechsel zu ermitteln, die von der Regierung angeboten wird und als solche nicht immer zu jedem Zeitpunkt verfügbar ist. Mit anderen Worten, die Bootstrapping-Technik wird verwendet, um die Renditen für Treasury-Zero-Coupon-Wertpapiere mit verschiedenen Laufzeiten zu interpolieren. Schatzwechsel gelten als risikofrei und werden daher zur Ableitung der Zinsstrukturkurve herangezogen. In diesem Artikel werden Bootstrapping-Beispiele erläutert.
Beispiele für Bootstrapping
Einige Beispiele für Bootstrapping sind unten aufgeführt:
Beispiel 1:
Nehmen wir das Beispiel von zwei 5% -Zinsen, die die Anleihe ohne Kreditausfallrisiko und mit einem Nennwert von 100 USD zu marktüblichen Preisen (ohne aufgelaufene Zinsen) von 99, 50 USD bzw. 98, 30 USD mit einer Laufzeit von 6 Monaten bezahlen bzw. 1 Jahr. Bestimmen Sie den Kassakurs für die 6-Monats- und 1-Jahres-Anleihe. Bitte beachten Sie, dass dies eine Par-Kurve ist, bei der der Kupon gleich der Rendite bis zur Fälligkeit ist.
Nach Ablauf von 6 Monaten zahlt die Anleihe einen Kupon von 2, 5 USD (= 100 USD * 5% / 2) zuzüglich des Nennbetrags (= 100 USD), der sich auf 102, 50 USD beläuft. Die Anleihe wird zu 99, 50 USD gehandelt. Daher kann der 6-Monats-Kassakurs S 0, 5y wie folgt berechnet werden:
€ 99, 50 = € 102, 50 / (1 + S 0, 5J / 2)
- S 5y = 6, 03%
Nach weiteren 6 Monaten zahlt die Anleihe einen weiteren Kupon von 2, 5 USD (= 100 USD * 5% / 2) zuzüglich des Nennbetrags (= 100 USD), der sich auf 102, 50 USD beläuft. Die Anleihe notiert bei 98, 30 USD. Daher kann der 1-Jahres-Kassakurs S 1y unter Verwendung von S 0, 5y als berechnet werden.
$ 99.50 = $ 2.50 / (1 + S 0.5y / 2) + $ 102.50 / (1 + S 1y / 2) 2
- $ 99, 50 = $ 2, 50 / (1 + 6, 03% / 2) + $ 102, 50 / (1 + S 1y / 2) 2
- S1y = 6, 80%
Entsprechend den Marktpreisen beträgt der Kassakurs für den ersten 6-Monats-Zeitraum 6, 03% und der Terminkurs für den zweiten 6-Monats-Zeitraum 6, 80%.


Beispiel 2:
Nehmen wir ein weiteres Beispiel für eine Kupon-Anleihe mit null Kreditausfallrisiko, die einen Nennwert von jeweils 100 USD hat und zum Nennwert gehandelt wird. Jede von ihnen hat jedoch eine unterschiedliche Laufzeit zwischen 1 Jahr und 5 Jahren. Bestimmen Sie den Kassakurs für alle Anleihen. Bitte beachten Sie, dass dies eine Par-Kurve ist, bei der der Kupon gleich der Rendite bis zur Fälligkeit ist. Die Einzelheiten sind in der folgenden Tabelle aufgeführt:
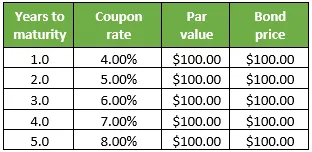
1. Am Ende eines Jahres zahlt die Anleihe einen Kupon von 4 USD (= 100 USD * 4%) zuzüglich des Nennbetrags (= 100 USD), der sich auf 104 USD beläuft, während die Anleihe zu 100 USD gehandelt wird. Daher kann der 1-Jahres-Kassakurs S 1y wie folgt berechnet werden:
$ 100 = $ 104 / (1 + S 1y )
- S1y = 4, 00%
2. Am Ende des 2. Jahres zahlt die Anleihe einen Kupon von 5 USD (= 100 USD * 5%) zuzüglich des Nennbetrags (= 100 USD), der sich auf 105 USD beläuft, während die Anleihe bei 100 USD gehandelt wird. Daher kann der 2-Jahres-Kassakurs S 2y unter Verwendung von S 1y als berechnet werden.
$ 100 = $ 4 / (1 + S 1y ) + $ 105 / (1 + S 2y ) 2
- $ 100 = $ 4 / (1 + 4, 00%) + $ 105 / (1 + S2y ) 2
- S1y = 5, 03%
3. Am Ende des dritten Jahres zahlt die Anleihe einen Kupon von 6 USD (= 100 USD * 6%) zuzüglich des Nennbetrags (= 100 USD), der sich auf 106 USD beläuft, während die Anleihe zu 100 USD gehandelt wird. Daher kann der 3-Jahres-Kassakurs S 3y unter Verwendung von S 1y und S 2y als berechnet werden.
$ 100 = $ 4 / (1 + S 1y ) + $ 5 / (1 + S 2y ) 2 + $ 106 / (1 + S 3y ) 3
- 100 $ = 4 $ / (1 + 4, 00%) + 5 $ / (1 + 5, 03%) 2 + 106 $ / (1 + S3y ) 3
- S 3y = 6, 08%
4. Am Ende des 4. Jahres zahlt die Anleihe einen Coupon von 7 USD (= 100 USD * 7%) zuzüglich des Nennbetrags (= 100 USD), der sich auf 107 USD beläuft, während die Anleihe bei 100 USD gehandelt wird. Daher kann der 4-Jahres-Kassakurs S 4y unter Verwendung von S 1y, S 2y und S 3y als berechnet werden.
$ 100 = $ 4 / (1 + S 1y ) + $ 5 / (1 + S 2y ) 2 + $ 6 / (1 + S 3y ) 3 + $ 107 / (1 + S 4y ) 4
- $ 100 = $ 4 / (1 + 4, 00%) + $ 5 / (1 + 5, 03%) 2 + $ 6 / (1 + 6, 08%) 3 + $ 107 / (1 + S 4y ) 4
- S 4y = 7, 19%
5. Am Ende des 5. Jahres zahlt die Anleihe einen Kupon von 8 USD (= 100 USD * 8%) zuzüglich des Nennbetrags (= 100 USD), der sich auf 108 USD beläuft, während die Anleihe bei 100 USD gehandelt wird. Daher kann der 5-Jahres-Kassakurs S 5y unter Verwendung von S 1y, S 2y, S 3y und S 4y als berechnet werden.
$ 100 = $ 4 / (1 + S 1y ) + $ 5 / (1 + S 2y ) 2 + $ 6 / (1 + S 3y ) 3 + $ 7 / (1 + S 4y ) 4 + $ 108 / (1 + S 5y ) 5
- $ 100 = $ 4 / (1 + 4, 00%) + $ 5 / (1 + 5, 03%) 2 + $ 6 / (1 + 6, 08%) 3 + $ 7 / (1 + 7, 19%) 4 + $ 108 / (1 + S 5y ) 5
- S 5y = 8, 36%
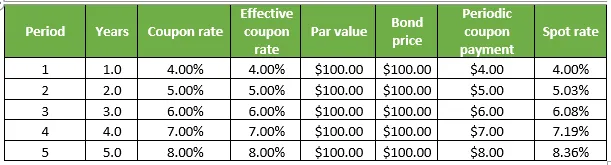

Fazit-Bootstrapping-Beispiele
Die Bootstrapping-Technik mag einfach sein, aber das Bestimmen und anschließende Glätten der realen Renditekurve kann eine sehr mühsame und komplizierte Aufgabe sein, die eine langwierige Mathematik erfordert, die hauptsächlich Anleihekurse, Kuponraten, Nennwerte und die Anzahl der Zinseszinszahlungen pro Jahr verwendet .
Empfohlene Artikel
Dies war eine Anleitung zu Bootstrapping-Beispielen. Hier diskutierten wir die Berechnung von Bootstrapping mit praktischen Beispielen. Sie können auch unsere anderen Artikelvorschläge durchgehen, um mehr zu erfahren -
- Was ist Bootstrap?
- Beispiel für die Globalisierung
- Monopolistische Wettbewerbsbeispiele
- Bootstrap vs jQuery UI