
Unterschied zwischen Z-Punktzahl und T-Punktzahl
Der Z-Score ist eine Konvertierung von Rohdaten in einen Standard-Score, wenn die Konvertierung auf dem Populationsmittelwert und der Populationsstandardabweichung basiert. Wenn ein vollständiger Datensatz bei uns verfügbar ist, können wir den Z-Score berechnen. Der Z-Score ist die Subtraktion des Populationsmittelwerts vom Roh-Score und dividiert das Ergebnis durch die Populationsstandardabweichung. T-Score ist eine Konvertierung von Rohdaten in den Standard-Score, wenn die Konvertierung auf dem Stichprobenmittelwert und der Stichprobenstandardabweichung basiert. Wenn der Populationsdatensatz nicht verfügbar ist, müssen wir einige Stichprobendaten abrufen, um den Stichprobenmittelwert und die Populationsstandardabweichung zu berechnen.
Z-Score
Bei einer Normalverteilung, bei der vollständige Daten verfügbar sind, ist dies eine Entfernung vom Mittelwert. Seine Formel lautet wie folgt:
Z= (x-μ)/σ
Wo,
X = einzelne Rohdaten
μ = Mittelwert der Grundgesamtheit
σ = Populationsstandardabweichung
T-Score
Der T-Score ist die Subtraktion der individuellen Standardabweichung vom individuellen Mittelwert und dividiert dann das Ergebnis durch das Gesamtergebnis der Stichprobenstandardabweichung multipliziert mit der Stichprobengröße. Seine Formel lautet wie folgt:
t = ((- μ)/s)*
= Mittelwert der Stichprobe
μ = Populationsmittelwert
s = Probenstandardabweichung
n = Stichprobengröße
Nehmen wir ein Beispiel, um dasselbe besser zu verstehen:
In einer Arbeit gibt es 3 Unterteilungen - I, II und III. Lassen Sie die Anzahl der Schüler, die richtig geantwortet haben, 25% sein, dh 75% sind nicht in der Lage, richtig zu antworten. Ebenso lassen 10% und 20% der Personen, die Abschnitt II und III richtig beantwortet hatten, darauf schließen, dass 90% und 80% Abschnitt II und III gefunden haben. Wir gehen davon aus, dass die an diesen drei Elementen gemessene Fähigkeit dieselbe ist und normal verteilt ist.
Die Punktzahl für jeden Schüler in einer Klasse wird verwendet, um den Mittelwert der Noten zu berechnen, der gleich 50 und einer Standardabweichung von 10 ist. Wir können die Z-Punktzahl mit der Punktzahl von 50 als (50-50) / 10 = 0 berechnen
Wir können interpretieren, dass die Schüler-Punktzahl 0 Abstand (in Einheiten von Standardabweichungen) vom Mittelwert beträgt, sodass der Schüler einen Durchschnitt erzielt hat.
Wenn die Punktzahl 60 ist, ist die Z-Punktzahl (60-50) / 10 = 1
Wir können interpretieren, dass der Schüler überdurchschnittlich gut abgeschnitten hat - ein Abstand von 1 Standardabweichung über dem Mittelwert.
Head to Head Vergleich zwischen Z score und T score (Infografiken)
Unten sehen Sie den 9 größten Unterschied zwischen dem Z-Score und dem T-Score 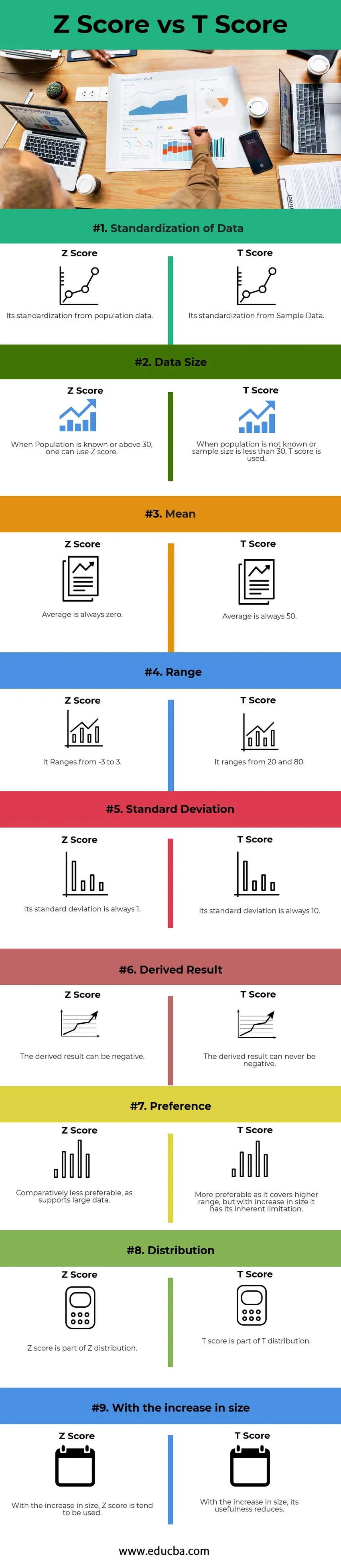
Hauptunterschiede zwischen Z-Punktzahl und T-Punktzahl
Lassen Sie uns einige der Hauptunterschiede zwischen dem Z-Score und dem T-Score diskutieren
- Der Z-Score ist die Standardisierung von den Populations-Rohdaten oder mehr als 30 Probendaten auf den Standard-Score, während der T-Score die Standardisierung von den Probendaten von weniger als 30 Daten auf den Standard-Score ist
- Der Z-Score reicht von -3 bis 3, während der T-Score von 20 bis 80 reicht.
- Mit zunehmender Datengröße ist die Verteilung in der Regel Z-Verteilung. Die Verteilung der beiden Z-Punkte und T-Punkte ist Teil einer Normalverteilung, sie unterscheiden sich jedoch je nach Größe
- In der Praxis wird der Z-Score in großem Umfang in Börsendaten und zur Überprüfung der Insolvenz eines Unternehmens verwendet, während der t-Score in großem Umfang zur Überprüfung der Knochenmineraldichte und der Bewertung des Frakturrisikos verwendet wird
Z score vs T score Vergleichstabelle
Schauen wir uns die 9 besten Vergleiche zwischen dem Z-Score und dem T-Score an
| Sr. No. | Vergleichspunkte | Z Score | T-Score |
| 1 | Standardisierung von Daten | Seine Standardisierung aus Bevölkerungsdaten | Seine Standardisierung aus Beispieldaten |
| 2 | Datengröße | Wenn die Bevölkerung bekannt ist oder über 30 liegt, kann man den Z-Score verwenden | Wenn die Population nicht bekannt ist oder die Stichprobengröße unter 30 liegt, wird der T-Score verwendet. |
| 3 | Bedeuten | Ein Durchschnitt ist immer Null. | Ein Durchschnitt ist immer 50. |
| 4 | Angebot | Es reicht von -3 bis 3. | Es reicht von 20 bis 80. |
| 5 | Standardabweichung | Die Standardabweichung ist immer 1 | Die Standardabweichung beträgt immer 10 |
| 6 | Abgeleitetes Ergebnis | Das abgeleitete Ergebnis kann negativ sein | Das abgeleitete Ergebnis kann niemals negativ sein |
| 7 | Präferenz | Vergleichsweise weniger bevorzugt, da große Datenmengen unterstützt werden | Stärker bevorzugt, da es einen höheren Bereich abdeckt, aber mit zunehmender Größe hat es seine inhärente Einschränkung |
| 8 | Verteilung | Die Z-Punktzahl ist Teil der Z-Verteilung | Der T-Score ist Teil der T-Verteilung |
| 9 | Mit der Vergrößerung | Mit zunehmender Größe wird in der Regel der Z-Score verwendet | Mit zunehmender Größe nimmt seine Nützlichkeit ab. |
Fazit
Sowohl der Z-Score als auch der T-Score sind Teil des Hypothesentests unter Normalverteilung. Wenn Sie eine Reihe von Messwerten für verschiedene Maße mithilfe von Z-Scores haben, können Sie feststellen, wie die Scores in ihren Verteilungen platziert sind. Dann kannst du sie vergleichen. Die Standardisierung von Ergebnissen ist ein weit verbreitetes Verfahren im Bereich der Forschung und Planung, da sie beim Vergleich verschiedener Testergebnisse hilfreich ist. Die Vereinheitlichung der Ergebnisse vor dem Kombinieren hilft einem Forscher, bessere und vergleichbare Ergebnisse zu erzielen.
Empfohlene Artikel
Dies war ein Leitfaden für den größten Unterschied zwischen dem Z-Score und dem T-Score. Hier diskutieren wir auch die wichtigsten Unterschiede zwischen Z-Score und T-Score mit Infografiken und Vergleichstabelle. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren.
- Finance vs Economics - Der größte Unterschied
- Defizit gegen Schulden - welches ist besser
- Kauf von Vermögenswerten im Vergleich zum Kauf von Aktien
- Geldmarkt gegen Kapitalmarkt
- Übersicht über den Altman Z Score