Gewichteter Durchschnitt in Excel (Inhaltsverzeichnis)
- Definition des gewichteten Durchschnitts
- Wie berechnet man den gewichteten Durchschnitt in Excel?
Einführung in den gewichteten Durchschnitt in Excel
Bei der Berechnung des arithmetischen Mittels oder des normalen Durchschnitts hat jede Zahl in einem Bereich die gleiche Bedeutung. Der Durchschnittswert oder das arithmetische Mittel wird berechnet, indem ein Zahlenbereich addiert und diese Summe durch die Anzahl der Werte im Bereich dividiert wird
Definition des gewichteten Durchschnitts
Der gewichtete Durchschnitt ist der Durchschnitt, bei dem einige Datenpunkte oder Zahlen als gewichtete Elemente berücksichtigt werden, um den Durchschnitt zu ermitteln. Statt dass jeder Datensatz gleich zum endgültigen Durchschnitt beiträgt, tragen einige Datenpunkte mehr als andere im gewichteten Durchschnitt bei.
Wie berechnet man den gewichteten Durchschnitt in Excel?
Schauen wir uns die verschiedenen verfügbaren Optionen an, um einen gewichteten Durchschnitt zu berechnen.
Sie können diese Excel-Vorlage mit gewichtetem Durchschnitt hier herunterladen - Excel-Vorlage mit gewichtetem DurchschnittBeispiel # 1 - Berechnung mit Hilfe der Summenfunktion
Die Summenfunktion wird zur Berechnung des gewichteten Durchschnitts verwendet, wenn die Tabelle eine geringere Anzahl von Datensätzen enthält.
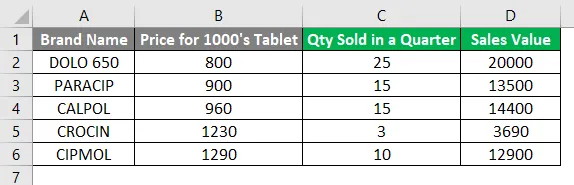
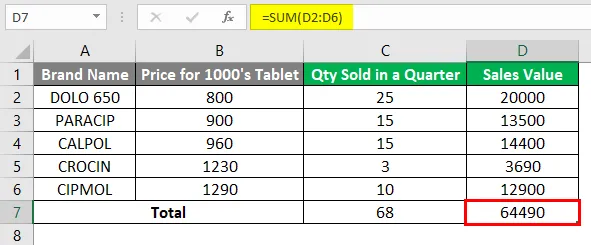
Im folgenden Beispiel habe ich einen Datensatz in Spalte A, der den Markennamen, Spalte B (Preis für jede Marke), Spalte C (verkaufte Menge) und Spalte D (Verkaufswert) enthält.
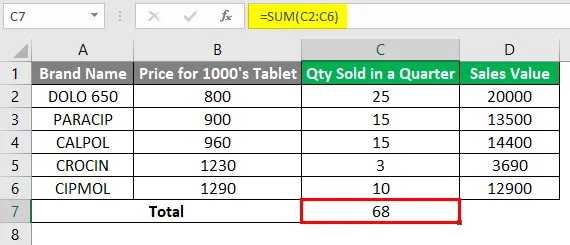
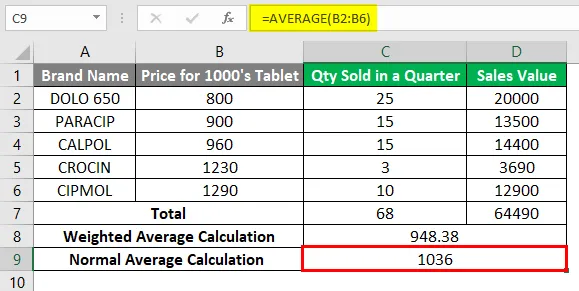
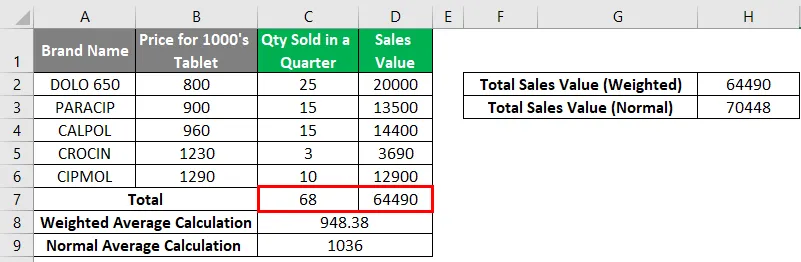
Zu Referenzzwecken können Sie zunächst die in der Zelle „C7“ verkaufte Gesamtmenge mit Hilfe der Summenfunktion zu Referenzzwecken berechnen. ie = SUMME (C2: C6) gibt einen Wert 68 zurück.
Ebenso können Sie mit Hilfe der SUMME-Funktion den Gesamtverkaufswert in der Zelle „D7“ berechnen.
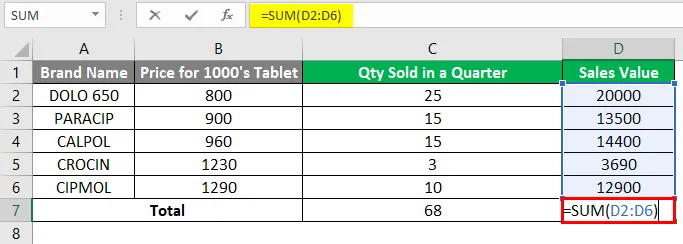
Wo es einen Gesamtverkaufswert von 64490 zurückgibt.
Hier muss ich den gewichteten Durchschnitt mit Hilfe der SUM-Funktion berechnen.
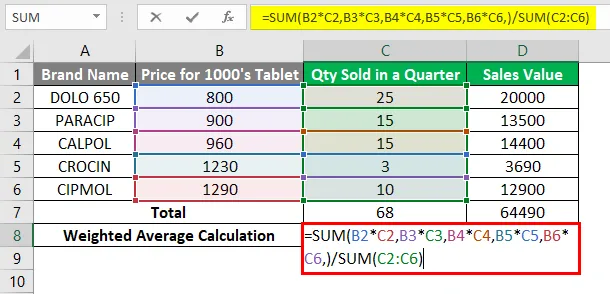
Das unten genannte Prinzip wird angewendet. Sie müssen jeden Wert (Preis der Marke) mit der entsprechenden verkauften Menge multiplizieren und dann alle Ergebnisse addieren. Später müssen Sie diese Antwort durch die Summe der verkauften Menge teilen. Wenden wir die Summenfunktion in der Zelle „C8“ an
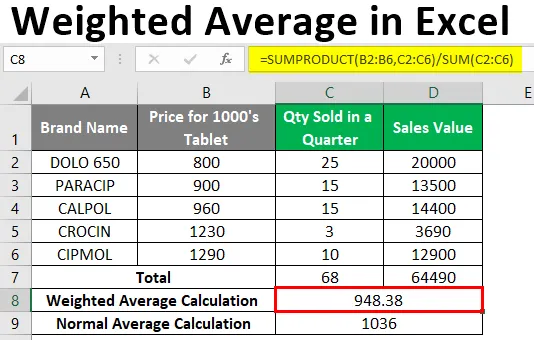
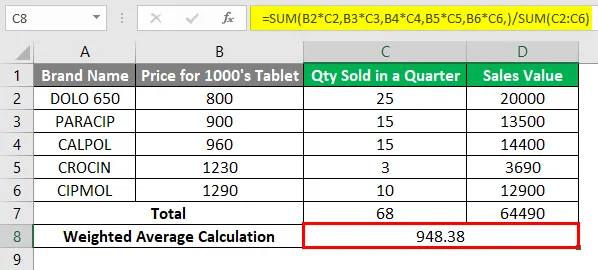
= SUMME (B2 · C2, B3 · C3, B4 · C4, B5 · C5, B6 · C6, ) / SUMME (C2: C6). Es gibt den gewichteten Durchschnittswert zurück, dh 948, 38.
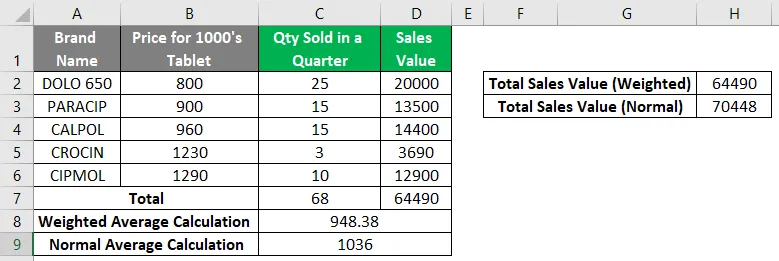
Um die Differenz zwischen normalem und gewichtetem Durchschnitt zu ermitteln, können Sie den normalen Durchschnitt in der Zelle C9 berechnen, dh = MITTELWERT (B2: B6) .
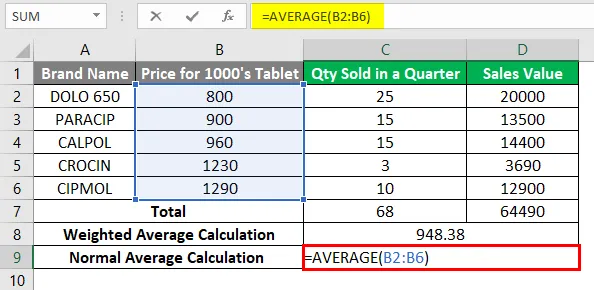
Es wird ein Wert von 1036 zurückgegeben.
Sie können den Genauigkeitsgrad beider Berechnungen, dh normaler und gewichteter Durchschnitt, wie unten beschrieben überprüfen. Wenn Sie 1036 (normaler Durchschnittswert) mit 68 (verkaufte Gesamtmenge) multiplizieren, erhalten Sie normalerweise 70448.
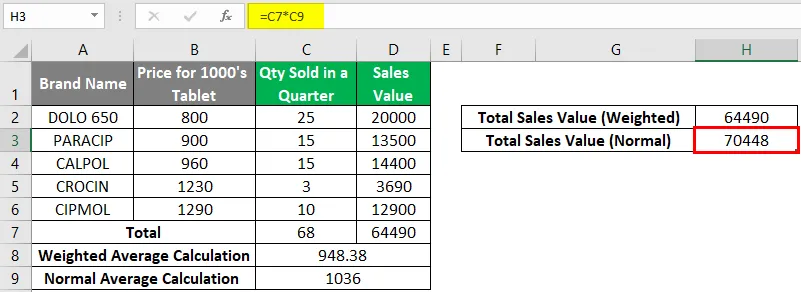
Dies entspricht nicht dem Gesamtverkaufswert (Zelle H2), aber wenn Sie 948, 38 (gewichteter Durchschnittswert) mit 68 (verkaufte Gesamtmenge) multiplizieren, erhalten Sie 64490, was dem Gesamtverkaufswert Zelle H3 entspricht.
Beispiel # 2 - Rechnen mit SUMPRODUCT und SUM-Funktion
SUMPRODUCT ermöglicht es Ihnen oder hilft Ihnen dabei, gewichtete Durchschnittsberechnungen effizient und schnell durchzuführen, wenn Sie mit einer großen Anzahl von Datensätzen arbeiten.
Im folgenden Beispiel habe ich einen Datensatz in Spalte A, der den Markennamen, Spalte B (Preis für jede Marke), Spalte C (verkaufte Menge) und Spalte D (Verkaufswert) enthält.
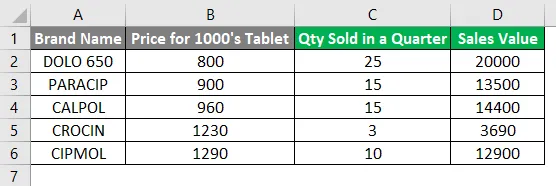
Hier muss ich mit Hilfe von SUMPRODUCT & SUM Function den gewichteten Durchschnitt berechnen. Die Funktion SUMPRODUCT multipliziert den Datensatz von zwei oder mehr Arrays und fügt dann die Produkte hinzu. Wenden wir sowohl das Summenprodukt als auch die Summenfunktion in der Zelle „C7“ an.
= SUMPRODUCT (B2: B6, C2: C6) / SUM (C2: C6) gibt den gewichteten Durchschnitt 948, 38 zurück.
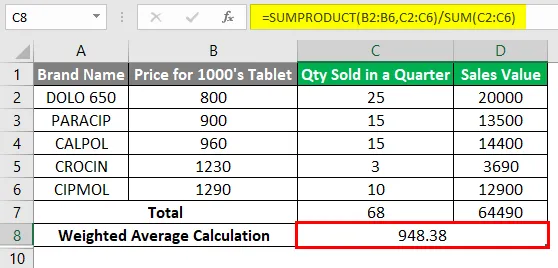
Wir können sehen, wie diese Formel mit einer Aufschlüsselung im Vergleich zum 1. Beispiel funktioniert. Anstatt also den Markenpreis mit der einzeln verkauften Menge zu multiplizieren, habe ich in der SUMPRODUCT-Funktion zwei Arrays angegeben (in diesem Fall ist ein Array ein kontinuierlicher Zellenbereich, dh zwei Arrays, ich habe Markenpreis und verkaufte Menge verwendet (B2: C2, B6: C6) und dividieren Sie das Ergebnis durch die Summe der verkauften Mengen.
Nachteil des gewichteten Mittelwerts : Summenfunktionen sind keine bessere Option zur Berechnung des gewichteten Mittelwerts, wenn Sie über eine große Anzahl von Datensätzen oder Elementen in einer Tabelle verfügen
Wissenswertes zum gewichteten Durchschnitt in Excel
- SUMPRODUCT liefert den #WERT! Fehlerwert, wenn die Array-Argumente unterschiedlich groß sind. Daher müssen alle Array-Argumente dieselbe Größe haben, oder in jedem Array sollte dieselbe Anzahl von Datensätzen vorhanden sein.
- Wenn die Datasets Textdaten in einem Bereich enthalten, werden diese von SUMPRODUCT als Nullen behandelt oder betrachtet.
Empfohlene Artikel
Dies ist eine Anleitung zum gewichteten Durchschnitt in Excel. Hier diskutieren wir, wie der gewichtete Durchschnitt in Excel berechnet wird, zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können auch unsere anderen Artikelvorschläge durchgehen -
- Aktivieren von eingebetteten Objekten in Excel
- So konsolidieren Sie Daten in mehreren Arbeitsblättern
- Anleitung zu COUNTIFS in Excel
- Excel-Hacks mit Excel-Tastenkombinationen