Gewichtete Durchschnittsformel - Rechner (Excel-Vorlage)

Gewichtete Durchschnittsformel (Inhaltsverzeichnis)

• Gewichtete Durchschnittsformel
• Gewichteter Durchschnittsrechner
• Gewichtete Durchschnittsformel in Excel (mit Excel-Vorlage)

Gewichtete Durchschnittsformel

Die Formel zur Berechnung des gewichteten Durchschnitts lautet wie folgt:

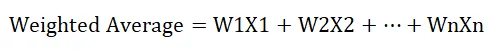
Wo,

• W bezeichnet das relative Gewicht (in%)
• X bezeichnet den Wert

Beispiele für gewichtete Durchschnittsformeln

Sehen wir uns einige Beispiele an, um die Formel für den gewichteten Durchschnitt zu verstehen:

Beispiel 1

Nehmen wir an, Anand hat das Geld in folgenden Anteilen investiert: 40% in Anlage A, 20% in Anlage B und 40% in Anlage C. Diese Anlagen haben folgende Rendite: Anlage A als 15%, Anlage B als 10 % und Investition C als 20%. Wir müssen einen gewichteten Durchschnitt für die Renditen berechnen, die Anand erhalten würde.

Hier,

• Wir haben relative Gewichte für die Anlagen A, B und C als 40%, 20% bzw. 40%.
• Der Wert (Rendite) für die Anlagen A, B und C beträgt 15%, 10% bzw. 20%.

Mit der Weighted Average Formula erhalten wir

• Gewichteter Durchschnitt = W1 X1 + W2 X2 + …… + Wn Xn
• Gewichteter Durchschnitt = 40% * 15% + 20% * 10% + 40% * 20%
• Gewichteter Durchschnitt = 16%

Dies zeigt, dass Anand eine durchschnittliche Rendite von 16% von den Anlagen A, B und C erhalten wird.

Beispiel # 2

Angenommen, Anand hat sich für einen Mathematikkurs eingeschrieben. Die Abschlussnote wird anhand der folgenden Kategorien ermittelt: Tests 30%, Abschlussprüfung 40%, Quiz 15% und Hausaufgaben 15%.

Anand hat in jeder Kategorie folgende Punkte erzielt: Tests-80, Abschlussprüfung-65, Tests-85, Hausaufgaben-90. Jetzt müssen wir die Gesamtnote von Anand herausfinden.

Um einen gewichteten Durchschnitt mit Prozentsätzen zu berechnen, muss jeder Kategoriewert zuerst mit seinem Prozentsatz multipliziert werden. Dann müssen alle diese neuen Werte addiert werden.

Hier,

Wir haben relative Gewichte für die folgenden Kategorien wie folgt:

• Tests 30%
• Abschlussprüfung 40%
• Tests 15%
• Hausaufgaben 15%

Und, Wert (Markierungen) für die Kategorien als

• Tests-80
• Abschlussprüfung-65,
• Quiz-85
• Hausaufgaben-90

Mit der Weighted Average Formula erhalten wir

• Gewichteter Durchschnitt = W1 X1 + W2 X2 + …… + WnXn
• Gewichteter Durchschnitt = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
• Gewichteter Durchschnitt = 76, 25 oder 76%

Dies zeigt, dass die Gesamtnote von Anand 76% beträgt .

Beispiel # 3

Nehmen wir an, Jagriti hat Geld in Aktien verschiedener Unternehmen investiert. Das Jagriti-Portfolio umfasst 30% auf Lager A, 15% auf Lager B, 30% auf Lager C und die verbleibenden 25% auf Lager D. Die erwartete Rendite gemäß der aktuellen Marktsituation für diese Aktien lautet wie folgt: Die Rendite auf Lager A beträgt 15%, Lagerrendite B 12%, Lagerrendite C 17% und Lagerrendite D 16%. Jagriti möchte ihre durchschnittliche Rendite des Portfolios anhand der aktuellen Marktsituation berechnen.

Hier,

• Wir haben die folgenden relativen Gewichte der Aktien im Portfolio: A, B, C & D als 30%, 15%, 30% bzw. 25%.
• Und Wert (Rendite) für die Aktien wie folgt: A, B, C & D als 15%, 12%, 17% bzw. 16%.

Mit der Weighted Average Formula erhalten wir

• Gewichteter Durchschnitt = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
• Gewichteter Durchschnitt = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
• Gewichteter Durchschnitt = 0, 154 oder 15, 4%

Dies zeigt, dass Jagriti eine durchschnittliche Rendite von 15, 4% aus dem Portfolio der Aktien A, B, C und D erzielen wird.

Erklärung der gewichteten Durchschnittsformel

Die gewichtete Durchschnittsformel wird zur Berechnung des Durchschnittswerts für eine bestimmte Menge von Zahlen mit unterschiedlichen Relevanzstufen verwendet. Die Gewichte müssen in Bezug auf die Gesamtrelevanz in Prozent angegeben werden. Die genommenen Gewichte sollten gleich 100% oder 1 sein.

Zur Berechnung der gewichteten Durchschnittsformel benötigen wir relative Gewichtung und Wert.

Die erste Komponente ist Relative Gewichtung und die zweite Komponente sind Werteingaben. Um den gewichteten Durchschnitt zu berechnen, müssen wir für jede als Wert genommene Variable eine spezifische Gewichtung festlegen und die Gewichtung muss 100% betragen.

Bedeutung und Verwendung der gewichteten Durchschnittsformel

Der gewichtete Durchschnitt wird in verschiedenen Finanzformeln verwendet. Einige Beispiele für ein gewichtetes durchschnittliches Beta und gewichtete durchschnittliche Kapitalkosten (WACC).

Wir sind mit der Idee vertraut, das athematische Mittel oder den Durchschnitt für eine Reihe von Elementen zu ermitteln. Wir können einfach die Werte aller Elemente addieren und durch die Gesamtzahl der Elemente dividieren, um den Durchschnitt zu berechnen. Dies funktioniert nur, wenn alle Artikel gleich gewichtet sind. Um beispielsweise die durchschnittlichen monatlichen Mobilfunkrechnungen für ein Jahr zu berechnen, können wir einfach die gesamten Rechnungsbeträge der letzten zwölf Monate addieren und durch zwölf dividieren. Dann erhalten wir eine ungefähre Vorstellung von der durchschnittlichen bezahlten Rechnung seit dem Mobilfunk Der Rechnungszyklus entspricht ungefähr dem gleichen Zeitraum, dh einem Monat.

Angenommen, Sie möchten die aktuelle durchschnittliche Kursnote in Ihrem Mathematikunterricht berechnen. Normalerweise weisen die meisten Klassen Prüfungen ein anderes Gewicht zu als Hausaufgaben, internen Tests und Wettbewerben. In diesem Fall müssen Sie einen gewichteten Durchschnitt berechnen, der das spezifische Gewicht für jedes Thema zur Berechnung Ihrer Kursnote verwendet.

Beispiel für einige Fälle, in denen ein gewichteter Durchschnitt anstelle eines einfachen Durchschnitts verwendet werden muss. Erster Fall - Wenn wir einen Durchschnitt mit unterschiedlichen Prozentwerten für verschiedene Kategorien berechnen möchten. Das obige Beispiel für die Kursnote ist einer der ähnlichen Fälle. Und zweitens, wenn wir eine große Gruppe von Gegenständen mit einer anderen Regelmäßigkeit haben.

Wenn ein Unternehmen aufgrund der Produktion eines saisonalen Produkts große Umsatzschwankungen aufweist, kann es die gewichtete Durchschnittsformel verwenden. Wenn das Unternehmen den Durchschnitt für seine variablen Ausgaben berechnen möchte, kann es die gewichtete Durchschnittsformel verwenden und den Umsatz als Gewicht verwenden, um ein besseres Verständnis für seine Ausgaben zu erhalten. Und kann die Menge vergleichen, die sie produzieren oder verkaufen.

Gewichteter Durchschnittsrechner

Sie können den folgenden gewichteten Durchschnittsrechner verwenden

W 1
X 1
W 2
X 2
W 3
X 3
W 4
X 4
Gewichtete Durchschnittsformel

Gewichtete Durchschnittsformel =	W 1 · X 1 + W 2 · X 2 + W 3 · X 3 + W 4 · X 4
	0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 =	0

Gewichtete Durchschnittsformel in Excel (mit Excel-Vorlage)

Hier machen wir dasselbe Beispiel für die Formel für den gewichteten Durchschnitt in Excel. Es ist sehr einfach und unkompliziert. Sie müssen die beiden Eingaben Relative Gewichte und Rendite bereitstellen.

Sie können den gewichteten Durchschnitt einfach mithilfe der Formel in der bereitgestellten Vorlage berechnen.

Die gewichteten Durchschnittsrenditen der Anlagen A, B und C werden wie folgt berechnet:

Die Gesamtnote von Anand wird wie folgt berechnet:

Gewicht Altersdurchschnittliche Renditen aus dem Aktienportfolio A, B, C und D werden wie folgt berechnet:

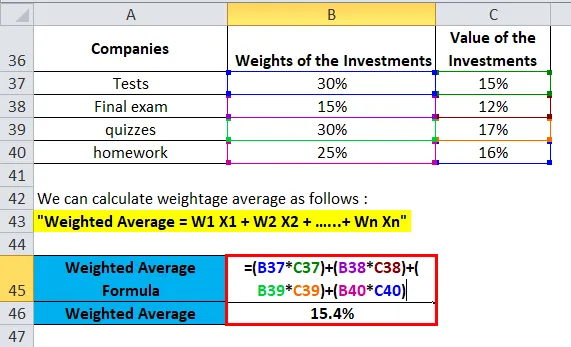
Sie können diese Excel-Vorlage für gewichtete Durchschnittsformeln hier herunterladen - Excel-Vorlage für gewichtete Durchschnittsformeln

Empfohlene Artikel

Dies war ein Leitfaden für eine gewichtete Durchschnittsformel. Hier diskutieren wir seine Verwendung zusammen mit praktischen Beispielen. Wir bieten Ihnen auch einen gewichteten Durchschnittsrechner mit herunterladbarer Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -

1. Wie berechnet man die Gemeinkostenquote?
2. Berechnen Sie den Equity Multiplikator mit Beispielen
3. Verwendung der Bruttogewinnmargenformel
4. Leitfaden zur Berechnung des Forderungsumsatzes