Excel NORMSINV (Inhaltsverzeichnis)
- Einführung in Excel NORMSINV
- Verwendung der NORMSINV-Formel in Excel
Einführung in Excel NORMSINV
Die Funktion Inverse kumulative Normalverteilung in Excel ist ein wichtiges Werkzeug, das die inverse kumulative Normalverteilung für einen bestimmten Wahrscheinlichkeitswert zurückgibt, dh normalerweise die Inverse der normalen kumulativen Normalverteilung (die einen Mittelwert von Null und eine Standardabweichung von Eins hat). Die NORM.S.INV-Funktion wird erstmals in der Microsoft Excel-Version 2010 eingeführt, bei der es sich um eine aktualisierte Version der NORMSINV-Funktion in Excel 2013 und der neuesten Version handelt. Die NORMSINV-Funktion wird hauptsächlich in der Kreditoren- und Finanzanalyse verwendet.
Syntax von Excel NORMSINV

Streit:
Wahrscheinlichkeit - Was nichts anderes als Wahrscheinlichkeit ist, entspricht der Normalverteilung.
Verwendung der NORMSINV-Formel in Excel
In Microsoft Excel ist die in NORMSINV integrierte Funktion in statistische Funktionen unterteilt, die im folgenden Screenshot dargestellt sind (in dem die Inverse der kumulativen Normalverteilung für eine bestimmte Wahrscheinlichkeit berechnet wird).
- Gehen Sie zum Menü Formeln.
- Klicken Sie auf Weitere Funktionen (siehe Abbildung unten).

- Wählen Sie eine statistische Kategorie aus, unter der sich die Funktion NORM.DIST befindet (siehe unten).
Beispiel # 1 - Verwenden von NORM.DIST und NORMSINV
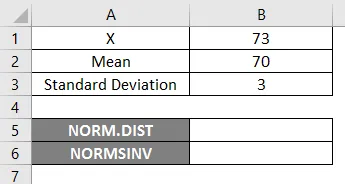
Um die NORM.DIST-Funktion zu verwenden, beginnen wir mit einem einfachen Beispiel, in dem wir die Noten der Schüler herausfinden müssen. Angenommen, wir haben die Klassenprüfung mit einer Durchschnittsnote von 70, dh mu = 70, und die Klassenstandardabweichung beträgt 3 Punkte, dh Sigma = 3 Hier müssen wir herausfinden, mit welcher Wahrscheinlichkeit die Schüler die Note 73 oder darunter erreicht haben, dh P (X <= 73). Schauen wir uns also an, wie Sie die Wahrscheinlichkeit mithilfe der NORM.DIST-Funktion ermitteln können.
- X = 3
- Mittelwert = 70
- Standardabweichung = 3
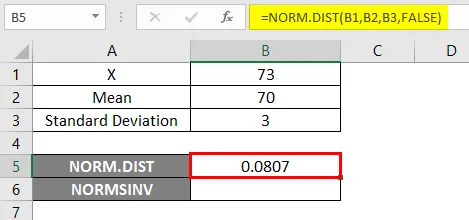
- Wenden Sie die NORM.DIST-Funktion wie folgt an.
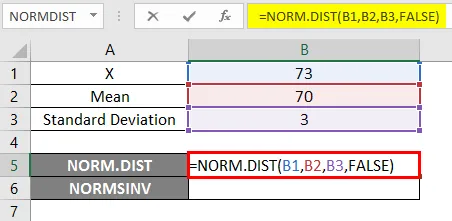
- Wenn wir die obige NORM.DIST-Funktion anwenden, erhalten wir die Wahrscheinlichkeit von 0.0807.
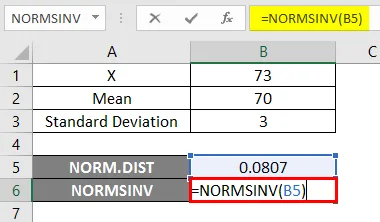
- Wenden Sie jetzt die NORMSINV-Funktion an, um die Umkehrung der kumulativen Normalverteilung wie unten gezeigt zu ermitteln.
Ergebnis -
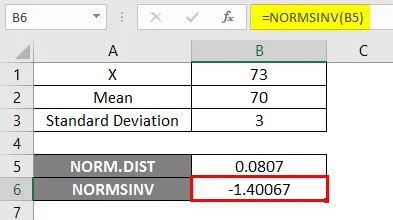
Im folgenden Ergebnis können wir sehen, dass wir für die angegebene Wahrscheinlichkeit negative Werte -1.40067 erhalten haben, dh eine Umkehrung der kumulativen Normalverteilung.
Beispiel # 2 - Mittlere und genaue Standardabweichung
Sehen wir uns ein weiteres Beispiel mit kurvenbasierten Daten an, um den Mittelwert und die genaue Standardabweichung zu ermitteln.
- Mittelwert = 7
- Standardabweichung = 1, 3
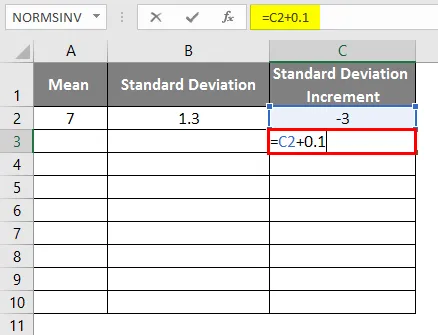
- Standardabweichungsinkrement als -3

- Um die Glockenkurve zu erhalten, müssen wir 0, 1 zum Standardabweichungsinkrement addieren, wobei die Daten wie unten gezeigt sind.
- Nach dem Anwenden der Formel ist das Ergebnis wie folgt.
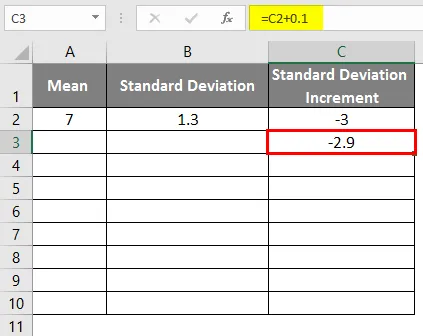
- Ziehen Sie die Werte, um mehr Werte zu erhalten, bis Sie die positiven Werte erhalten, sodass Sie eine linke Kurve erhalten.
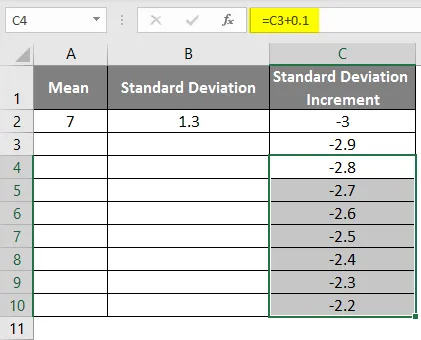
- Um die richtige Kurve zu erhalten, müssen wir die Formel als = mittlere Standardabweichung * 3 anwenden, damit wir die genauen Kurven erhalten.
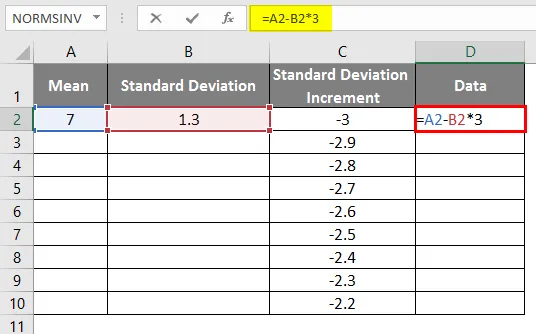
- Nach Verwendung der Formel wird das Ergebnis unten angezeigt.
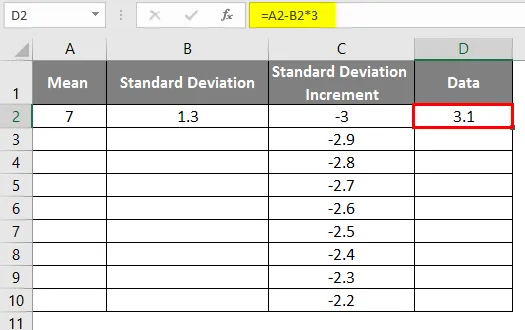
- Wie in den obigen Daten für das Inkrementieren der Standardabweichung, um die linke Kurve zu erhalten, haben wir die Werte um 0, 1 inkrementiert
- Das gleiche Szenario wird durch Anwenden der Formel als = 3.1 + STANDARDABWEICHUNG / 10 verwendet, um das Kurveninkrement 0, 1 zu erhalten
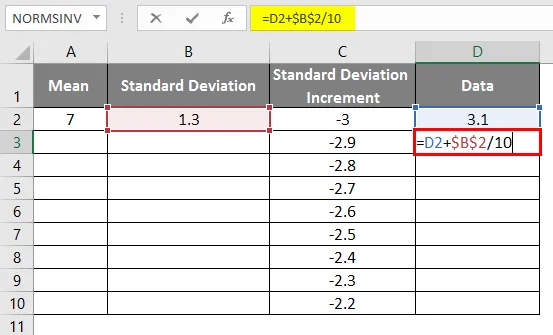
- Nach Verwendung der Formel wird das Ergebnis unten angezeigt.

- Ziehen Sie die Werte, um das genaue Ergebnis zu erhalten, das im folgenden Screenshot gezeigt wird.
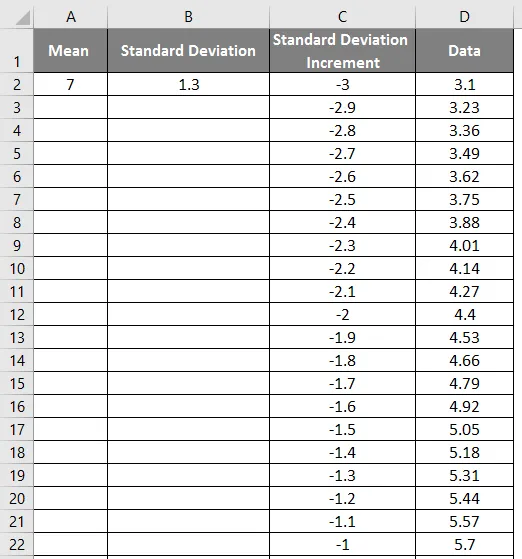
- Wenden Sie nun die Normalverteilungsfunktion mit der Formel = NORM.DIST an (DATA-Wert, Mittelwert, Standardabweichung, falsch).
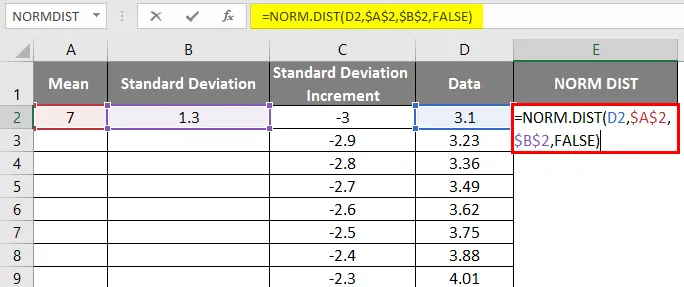
- Wir werden das folgende Ergebnis wie folgt erhalten.
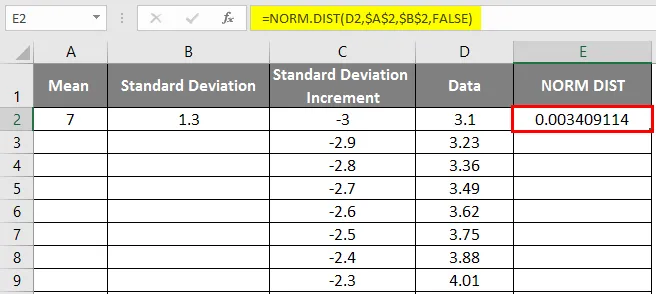
- Ziehen Sie die Werte, um das genaue unten gezeigte Ergebnis zu erhalten.
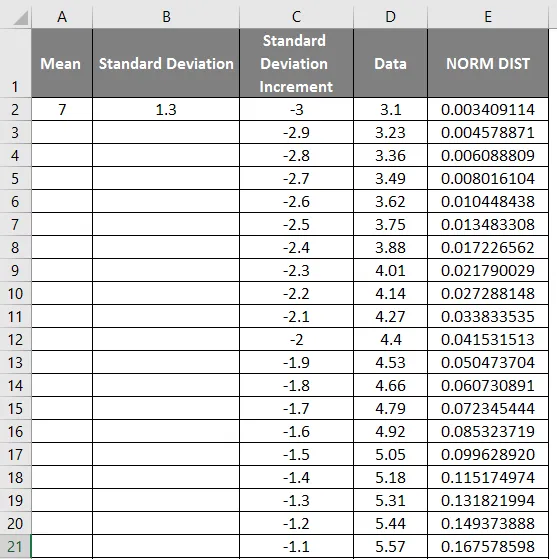
- Wie wir im obigen Screenshot sehen können, haben wir die NORMALE Verteilung aus dem Mittelwert und der Standardabweichung berechnet. Schauen wir uns nun die Umkehrung der NORMAL-Verteilung an, indem Sie das unten gezeigte NORMSINV anwenden.
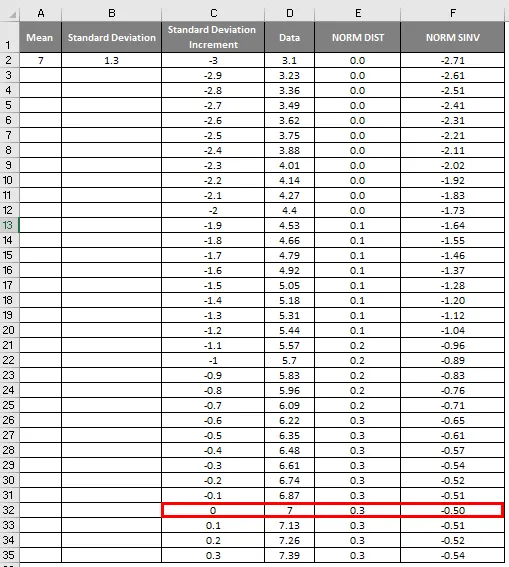
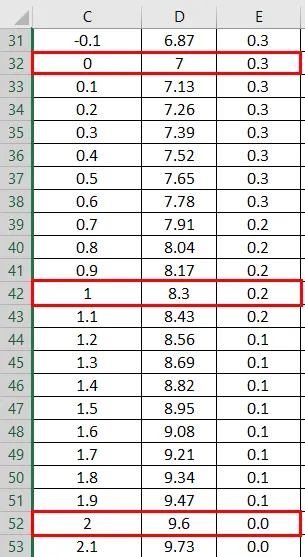
- Hier sehen wir, dass der Wert Null (0) eine Standardabweichung von 7 hat.

Anwenden eines Streudiagramms, um die Darstellung der linken und rechten Kurve zu überprüfen.
- Wählen Sie zuerst die Daten und die Spalte Normal aus.
- Gehen Sie zur Registerkarte Einfügen und wählen Sie das Streudiagramm wie folgt aus.
- Wir werden das unten gezeigte Kurvendiagramm erhalten.
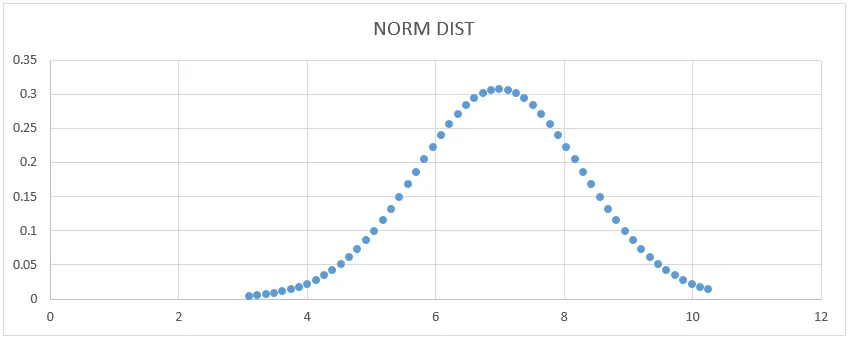
Hier können wir sehen, dass der Mittelwert 7 eine Standardabweichungsform hat, bei der wir dies durch Zeichnen einer geraden Linie zur Darstellung zeigen können.
- Mittelwert = 7
- 1 –Standardabweichung gibt 68% der Daten an.
- 2 –Standardabweichung gibt 95% der Daten an.
- 3 –Standardabweichung gibt 99, 7% der Daten an.
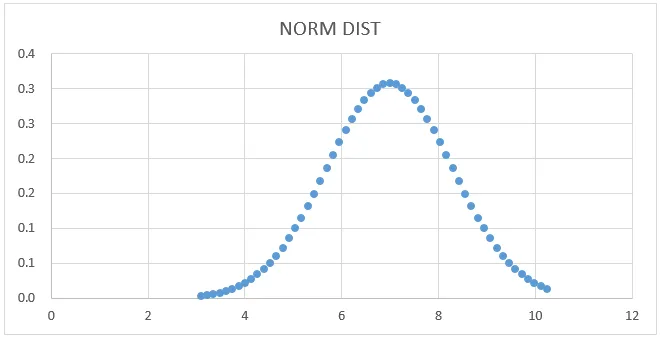
Normalverteilungsdiagramm:
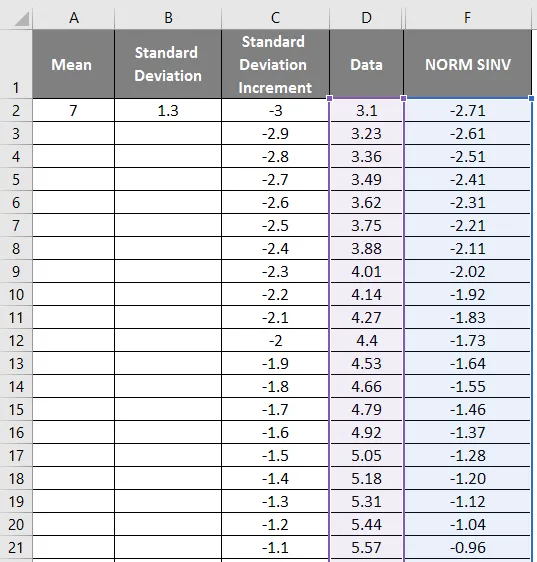
NORMSINV-Grafik:
Wählen Sie nun aus der obigen Abbildung die Datenspalte und NORM SINV aus, um die folgende Grafik zu erhalten.
- Wählen Sie zuerst die Daten und die Spalte Normal aus.
- Gehen Sie zur Registerkarte Einfügen und wählen Sie das Streudiagramm aus.
- Wir erhalten die folgende Grafik, die im folgenden Screenshot gezeigt wird.
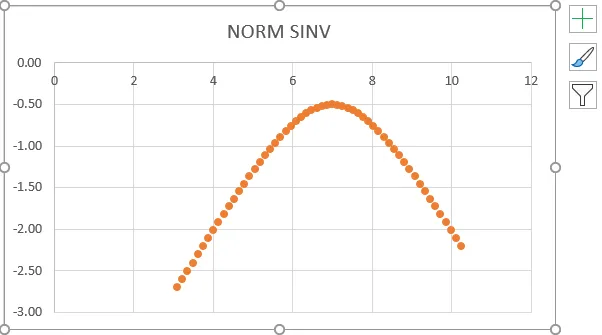
- Aus dem obigen Screenshot können wir ersehen, dass wir eine genaue Umkehrung einer Normalverteilung erhalten haben, die den gleichen Wert wie unten zeigt.

Beispiel # 3 - Konfiguration der linken und rechten Kurve
In diesem Beispiel konfigurieren wir die linke und rechte Kurve mit der Normalverteilungsfunktion. Betrachten Sie die folgenden Daten wie unten gezeigt, wobei x negative Werte hat und auf positive Werte inkrementiert wird.
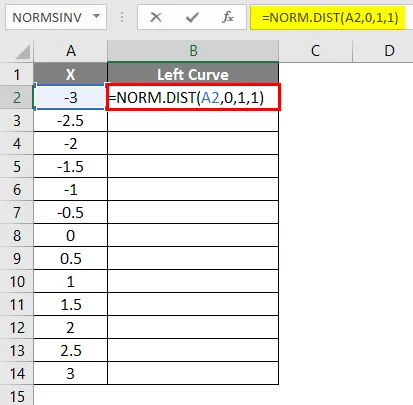
- Wenden Sie die Formel = NORM.DIST (A2, 0, 1, 1) an.
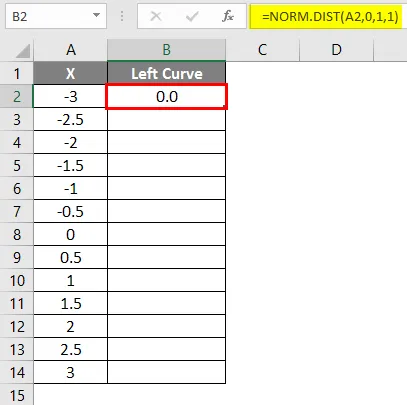
- Nach dem Anwenden der Formel wird das Ergebnis unten angezeigt.
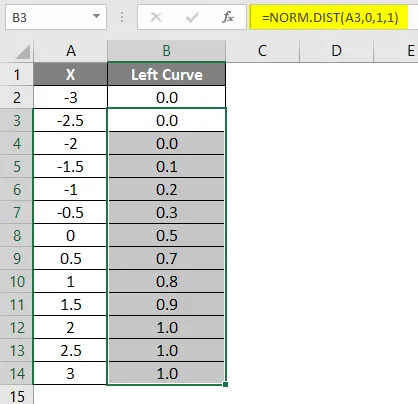
- Ziehen Sie die Formel in andere Zellen.
- Wende Formel = 1-B2 an .
- Nach dem Anwenden der Formel wird das Ergebnis unten gezeigt.
- Ziehen Sie dieselbe Formel in andere Zellen.
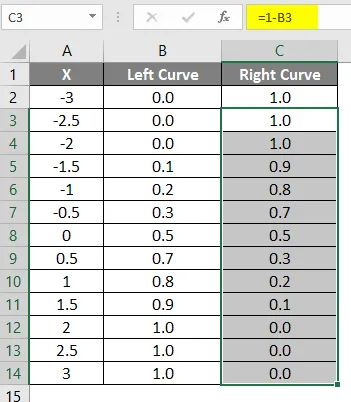
Das Ergebnis der oben angewendeten Formel ist unten gezeigt.
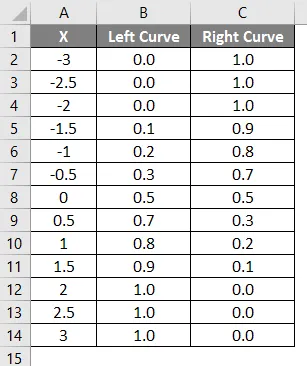
- Die Werte der linken Kurve wurden berechnet, indem die Formel NORMAL DISTRIBUTION angewendet wurde, indem der kumulative Wert auf True gesetzt wurde, und die NORMSINV wurde unter Verwendung der linken Kurve berechnet.
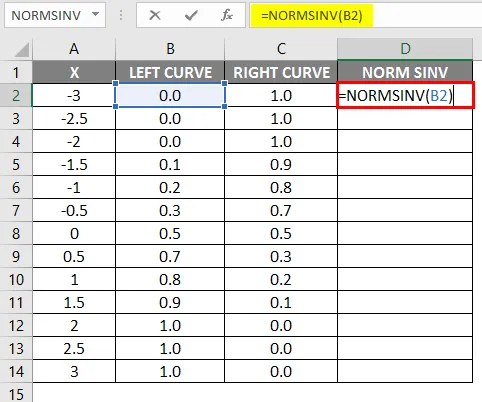
- Nach dem Anwenden der Formel wird das Ergebnis unten angezeigt.
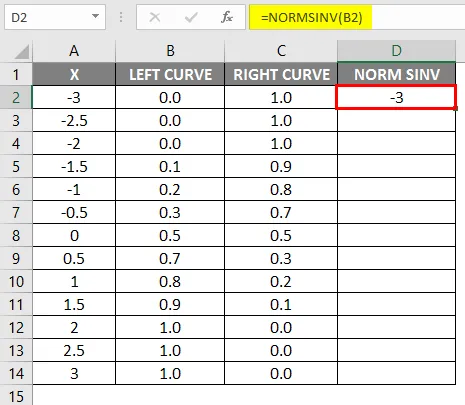
- Ziehen Sie dieselbe Formel in andere Zellen.
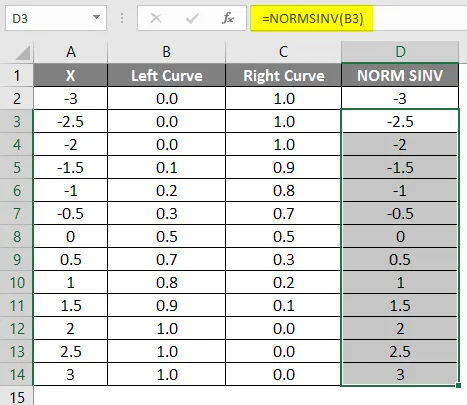
Wie wir sehen können, haben wir den gleichen Wert für NORMSINV, der nichts anderes als die Umkehrung der Normalverteilung ist. Auf die gleiche Weise erhalten wir den Wert für die rechte Kurve, indem wir den Wert für die 1-linke Kurve berechnen. Im nächsten Schritt werden wir anhand des Streudiagramms überprüfen, wie wir die Höhe des x erhalten.
- Wählen Sie die linke und rechte Kurvenspalte aus.
- Gehe zum Menü Einfügen.
- Wählen Sie das Streudiagramm wie folgt aus.
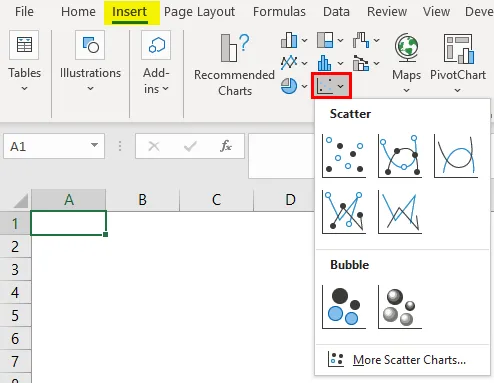
Wir werden das untenstehende Grafikergebnis erhalten, wie unten gezeigt.
NORM SINV Graph:
In der folgenden Grafik können wir sehen, dass die linke Kurve des NORM DISTRIBUTION-Werts die exakte Übereinstimmung für (0, 0, 5) hat, die in der Mitte der Linie liegt, wo wir dieselbe Grafik erhalten, wenn wir NORMDIST anwenden.
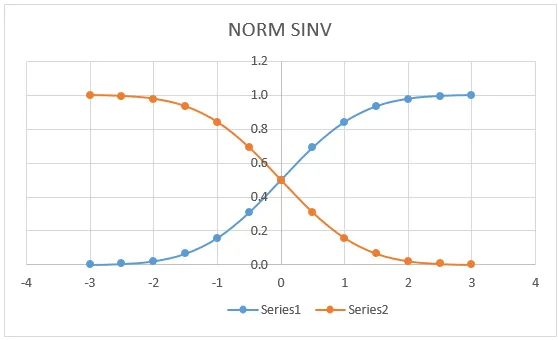
Hier in der obigen Grafik zeigt es sehr deutlich, dass wir den exakten Mittelwert an einem Mittelpunkt haben, der bedeutet:
- X = 0
- Linkskurve = 0, 5
- Rechte Kurve = 0, 5
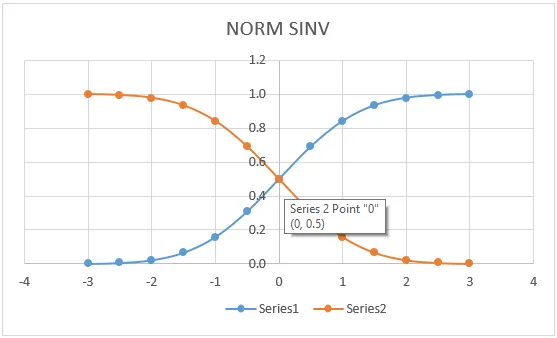
Wir haben es angezeigt, um die NORMSINV-Werte in einem grafischen Format wie unten dargestellt anzuzeigen.
Wichtige Informationen zu Excel NORMSINV
- #Wert! Ein Fehler tritt auf, wenn das angegebene Argument ein nicht numerischer oder logischer Wert ist.
- In der Normalverteilungsfunktion erhalten wir normalerweise #NUM! Fehler aufgrund des Standardabweichungsarguments ist kleiner oder gleich Null.
Empfohlene Artikel
Dies ist eine Anleitung zu Excel NORMSINV. Hier besprechen wir die Verwendung von NORMSINV in Excel zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können auch unsere anderen Artikelvorschläge durchgehen -
- Wie benutze ich das Namensfeld in Excel?
- Arbeiten mit Matrix in Excel
- Was ist, wenn Analyse in Excel
- Barwertformel in Excel