
Z Score Formula (Inhaltsverzeichnis)
- Formel
- Beispiele
- Taschenrechner
Was ist die Z-Score-Formel?
Der „Z-Score“ ist eines der am häufigsten verwendeten statistischen Tools zur Standardisierung des Scores, vorausgesetzt, die Populationsmittel und die Standardabweichung sind bekannt. Daher wird der Z-Score auch als Standard-Score bezeichnet. Der Z-Wert variiert im Bereich des -3-fachen der Standardabweichung bis zum +3-fachen der Standardabweichung mit einem Mittelwert von Null und einer Standardabweichung von Eins. Die Formel für den Z-Wert einer Variablen kann abgeleitet werden, indem der Mittelwert der Grundgesamtheit von der angegebenen Variablen (die Teil des Datensatzes oder der Grundgesamtheit ist) abgezogen und das Ergebnis durch die Standardabweichung der Grundgesamtheit dividiert wird. Mathematisch wird es dargestellt als
Z = (X – μ) / σ
wo,
- X = Variabel aus der Grundgesamtheit
- μ = Mittelwert der Bevölkerung
- σ = Standardabweichung der Grundgesamtheit
Beispiele für Z-Score-Formeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des Z-Scores besser zu verstehen.
Sie können diese Excel-Vorlage für Z-Score-Formeln hier herunterladen - Excel-Vorlage für Z-Score-FormelnZ Score Formula - Beispiel # 1
Nehmen wir das Beispiel von Manny, der kürzlich für SAT erschienen ist. Bei diesem Versuch erzielte er 1109 Punkte. Nach den verfügbaren Informationen lag der durchschnittliche SAT-Wert bei 1030 mit einer Standardabweichung von 250. Berechnen Sie den Z-Wert für Mannys SAT-Wert und bewerten Sie, wie gut er im Vergleich zu den durchschnittlichen Testteilnehmern abgeschnitten hat.
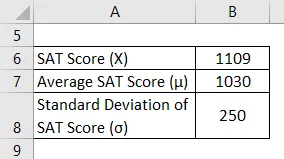
Lösung:
Der Z-Score wird nach der unten angegebenen Formel berechnet
Z = (X - & mgr;) / & sgr ;.
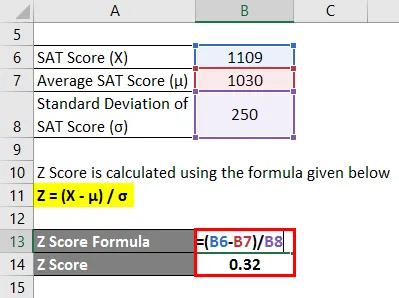
- Z Score = (1109 - 1030) / 250
- Z Score = 0, 32
Daher ist der SAT-Wert von Manny um 0, 32 Standardabweichung höher als der durchschnittliche Wert der Testteilnehmer, was darauf hinweist, dass 62, 55% der Testteilnehmer weniger Punkte als Manny erzielten.
Z Score Formula - Beispiel # 2
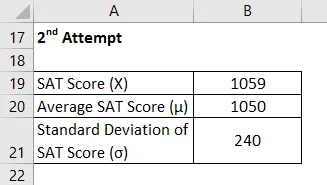
Nehmen wir nun das Beispiel von Chelsea, die den SAT zweimal geschrieben hat und ihre Leistung darin vergleichen möchte. Sie schaffte es, 1085 und 1059 in ihrem 1. und 2. Versuch zu erzielen. Nach den verfügbaren Informationen betrugen die durchschnittliche Punktzahl und die Standardabweichung während des ersten Versuchs 1100 bzw. 230, während sie in letzterem 1050 bzw. 240 betrugen. Bitte helfen Sie Chelsea bei der Entscheidung, in welcher Prüfung sie bessere Leistungen erbracht hat.
Lösung:
1. Versuch
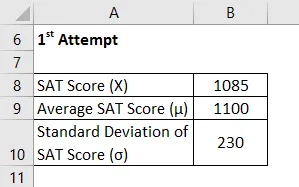
Der Z-Score wird nach der unten angegebenen Formel berechnet
Z = (X - & mgr;) / & sgr ;.
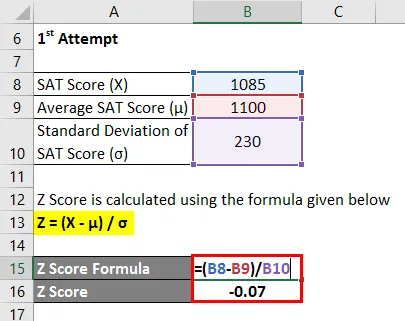
- Z Score = (1085 - 1100) / 230
- Z Score = -0, 07
Daher liegt die SAT-Punktzahl von Chelsea im ersten Versuch um 0, 07 Standardabweichung unter der durchschnittlichen Punktzahl der Testteilnehmer, was darauf hinweist, dass 47, 40% der Testteilnehmer im ersten Versuch weniger Punkte als Chelsea erzielten.
2. Versuch
Der Z-Score wird nach der unten angegebenen Formel berechnet
Z = (X - & mgr;) / & sgr ;.
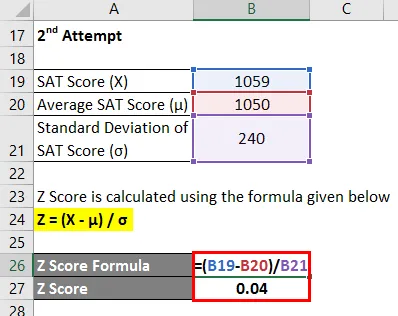
- Z Score = (1059 - 1050) / 240
- Z Score = 0, 04
Daher ist die SAT-Punktzahl von Chelsea im 2. Versuch um 0, 04 Standardabweichung höher als die durchschnittliche Punktzahl der Testteilnehmer, was darauf hinweist, dass 51, 50% der Testteilnehmer im 2. Versuch weniger Punkte als Chelsea erzielten.
Aus dem Vergleich der Z-Werte geht hervor, dass Chelsea bei ihrem zweiten Versuch eine bessere Leistung erbracht hat .
Erläuterung
Die Formel für die Z-Bewertung kann mithilfe der folgenden Schritte abgeleitet werden:
Schritt 1: Bauen Sie zunächst eine Population mit einer großen Anzahl von Variablen auf, und die Variablen werden mit X i bezeichnet .
Schritt 2: Als nächstes wird die Anzahl der Variablen in der Population berechnet und mit N bezeichnet.
Schritt 3: Als nächstes wird der Mittelwert der Grundgesamtheit berechnet, indem alle Variablen summiert werden, gefolgt von einer Division durch die Gesamtzahl der Variablen (Schritt 2) im Datensatz. Der Mittelwert der Bevölkerung wird mit μ bezeichnet.
μ = ∑ X i / N
Schritt 4: Ziehen Sie als Nächstes den Mittelwert von jeder Variablen des Datensatzes ab, um deren Abweichung vom Mittelwert zu berechnen.
dh (X i - μ) ist die Abweichung für den i- ten Datenpunkt.
Schritt 5: Berechnen Sie als nächstes die quadratischen Abweichungen für die Variablen, dh (X i - μ) 2 .
Schritt 6: Addieren Sie als Nächstes alle quadratischen Abweichungen und dividieren Sie dann die Summe durch die Anzahl der Variablen im Datensatz, um die Varianz zu ermitteln.
σ 2 = ∑ (X i - μ) 2 / N
Schritt 7: Als nächstes wird die Standardabweichung der Grundgesamtheit berechnet, indem die Quadratwurzel der im obigen Schritt berechneten Varianz berechnet wird.
σ = √ ∑ (X i - μ) 2 / N
Schritt 8: Abschließend wird die Formel für den Z-Score abgeleitet, indem der Mittelwert der Grundgesamtheit (Schritt 3) von der Variablen abgezogen und das Ergebnis durch die Standardabweichung der Grundgesamtheit (Schritt 7) dividiert wird (siehe unten).
Z = (X - & mgr;) / & sgr ;.
Relevanz und Verwendung der Z-Score-Formel
Aus Sicht eines Statistikers ist das Konzept des Z-Scores sehr wichtig, da es hilfreich ist, um die Wahrscheinlichkeit zu bestimmen, ob ein Ereignis innerhalb einer Normalverteilung auftritt oder nicht. Tatsächlich wird der Z-Score auch verwendet, um zwei Roh-Scores aus zwei verschiedenen Normalverteilungen zu vergleichen, und zwar durch Konvertieren der Roh-Scores in einen Z-Score oder einen standardisierten Score. Weiterhin impliziert ein positiver Z-Score einen Score, der höher als der Mittelwert ist, während ein negativer Z-Score einen Score impliziert, der niedriger als der Mittelwert ist.
Z Score Formelrechner
Sie können den folgenden Z-Score-Formelrechner verwenden
| X | |
| µ | |
| σ | |
| Z | |
| Z = |
|
|
Empfohlene Artikel
Dies war ein Leitfaden für die Z-Score-Formel. Hier besprechen wir die Berechnung des Z-Scores zusammen mit praktischen Beispielen. Wir bieten auch einen Z-Score-Rechner mit herunterladbarer Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Beispiele für die Formel für die Stichprobengröße
- Wie berechnet man den gewichteten Mittelwert?
- Rechner für Korrelationsformel
- Formel zur Berechnung der Normalverteilung
- Beispiele für Altman Z Score