
Exponential Growth Formula (Inhaltsverzeichnis)
- Exponential Growth Formula
- Beispiele für Exponential Growth Formula (mit Excel-Vorlage)
- Exponentieller Wachstumsrechner
Exponential Growth Formula
Exponentielles Wachstum und Zerfall sind die beiden Funktionen, um das Wachstum und den Zerfall in einem festgelegten Muster zu bestimmen. Exponentielle Wachstums- und Zerfallsformeln können in einer bestimmten Situation verwendet werden, wenn eine Größe in regelmäßigen Abständen wächst. Das Funktionsmuster kann dargestellt und in einer algebraischen Gleichung zusammengefasst werden.
Die Exponentialwachstumsformel kann genannt werden als:
Exponential Growth (y) = a * (1 + r) ^x
Während auf der anderen Seite exponentielle Zerfallsformel genannt werden kann als
Exponential Decay (y) = a * (1 – r) ^x
Wobei die folgenden ganzen Zahlen angegeben werden können als:
- a = Anfangswachstum (die Menge vor dem Messen des Wachstums oder des Zerfalls)
- r = Wachstums- oder Abklingrate (am häufigsten als Prozentsatz dargestellt und als Dezimalzahl ausgedrückt)
- x = Anzahl der abgelaufenen Zeitintervalle
Beispiele für Exponential Growth Formula (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung des exponentiellen Wachstums besser zu verstehen.
Sie können diese Excel-Vorlage für exponentielles Wachstum hier herunterladen - Excel-Vorlage für exponentielles WachstumExponentielles Wachstum - Beispiel # 1
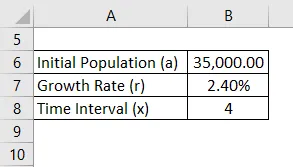
Die Einwohnerzahl einer Heimatstadt in Schottland wurde im Jahr 2019 auf 35.000 geschätzt. Es wird erwartet, dass die Bevölkerung jedes Jahr um 2, 4% wächst. Wie hoch ist der Wachstumsfaktor der Heimatstadt in Schottland und anhand der Schätzung wird die Bevölkerung der Heimatstadt für die nächsten 4 Jahre berechnet?
Lösung:
Das exponentielle Wachstum wird mit der unten angegebenen Formel berechnet
Exponentielles Wachstum (y) = a * (1 + r) x
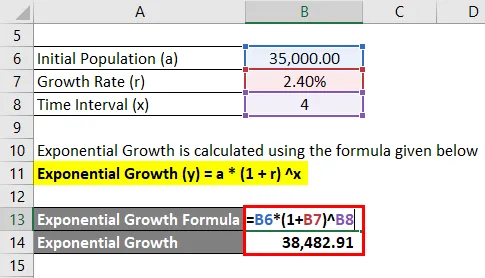
- Exponentielles Wachstum = 35.000 * (1+ 2, 4%) 4
- Exponentielles Wachstum = 38.482, 91
Das exponentielle Wachstum beträgt 38.482, 91
Exponentielles Wachstum - Beispiel 2
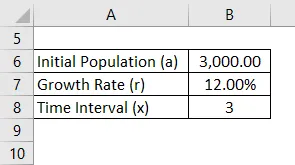
Im Jahr 2021 leben in einem kleinen abgelegenen Dorf in der Nähe des Himachal-Gebiets etwa 3000 Einwohner. Die durchschnittliche jährliche Wachstumsrate der Bevölkerung in den letzten 3 Jahren beträgt 12% pro Jahr. Wie viele Einwohner werden nach 10 Jahren im Dorf sein? Notwendigkeit, den Wert durch das exponentielle Wachstum zu berechnen.
Lösung:
Das exponentielle Wachstum wird mit der unten angegebenen Formel berechnet
Exponentielles Wachstum (y) = a * (1 + r) x
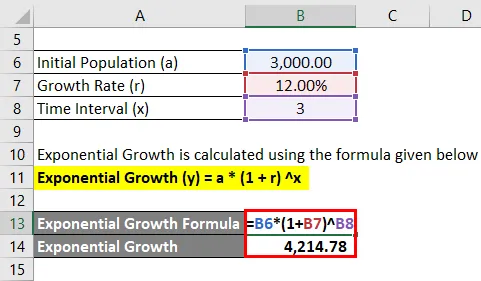
- Exponentielles Wachstum = 3.000 * (1 + 12%) 3
- Exponentielles Wachstum = 4.214, 78
Das exponentielle Wachstum beträgt 4.214, 78.
Exponentielles Wachstum - Beispiel # 3
Eine bestimmte Art von Bakterien wächst bei einer günstigen Wachstumsrate von 10%. Angesichts der Tatsache, dass es zu Beginn ungefähr 100 Bakterien gab, wie viele Bakterien wird es in anderthalb Tagen geben?
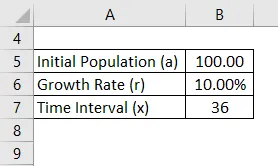
Lösung:
Das exponentielle Wachstum wird mit der unten angegebenen Formel berechnet
Exponentielles Wachstum (y) = a * (1 + r) x
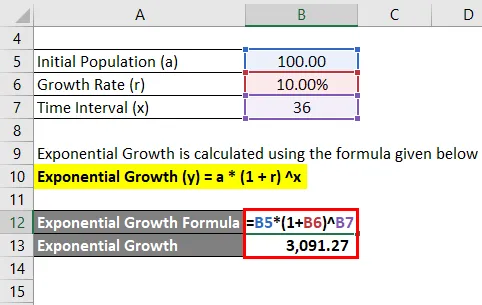
- Exponentielles Wachstum = 100 * (1 + 10%) 36
- Exponentielles Wachstum = 3.091, 27
Das exponentielle Wachstum beträgt 3.091, 27.
Erläuterung
Die Formel wird verwendet, wenn eine bestimmte Variable kontinuierlich wächst, z. B. das Bevölkerungswachstum, das Bakterienwachstum, wenn die Menge oder die Variable um einen festen Prozentsatz wächst, kann sich die Exponentialformel als nützlich erweisen, um in der Statistik verwendet zu werden
Relevanz und Verwendung der Exponential Growth Formula
- Das Konzept des exponentiellen Wachstums wird hauptsächlich im Konzept der Modellierung und des Wirtschaftswachstums verwendet. Wenn wir herausfinden wollen, wie hoch der Umsatz des Unternehmens ist, wenn es mit einer konstanten Wachstumsrate von x% wächst, verwenden wir häufig das exponentielle Wachstum und sein Konzept, um den Umsatz des Unternehmens zu bestimmen, das mit einem bestimmten Prozentsatz von wächst Wachstumsrate
- Die Exponentialfunktion tritt auch in einer Vielzahl von Zusammenhängen in Physik, Chemie, Ingenieurwesen, mathematischer Biologie und Wirtschaft auf und ist auch in natur- und sozialwissenschaftlichen Konzepten weit verbreitet
- Die Exponentialformel ist auch in der Mathematik eine wichtige Funktion und wurde nur mit Hilfe der Mathematik und der Wirtschaft abgeleitet. Die exponentielle Zerfallsformel eignet sich für eine Vielzahl von Anwendungen in der Praxis, insbesondere zum Verfolgen von Inventar, das regelmäßig in der gleichen Menge verwendet wird (wie Lebensmittel für eine Schulkantine), und ist besonders nützlich für die schnelle Beurteilung der Langzeitergebnisse Nutzungskosten eines Produkts im Laufe der Zeit
Exponentieller Wachstumsrechner
Sie können den folgenden Exponential Growth Calculator verwenden
| ein | |
| r | |
| x | |
| Exponential Growth (y) Formula | |
| Exponentielles Wachstum (y) Formel = | a * (1 + r) x |
| = | 0 * (1 + 0) 0 = 0 |
Empfohlene Artikel
Dies war ein Leitfaden für die Exponential Growth-Formel. Hier diskutieren wir die Berechnung des exponentiellen Wachstums zusammen mit praktischen Beispielen. Wir bieten auch einen Exponential Growth-Rechner mit herunterladbarer Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- Leitfaden zur Gordon-Wachstumsmodellformel
- Wie berechnet man den Deckungsbeitrag?
- Formel für das Nettoeinkommen
- Berechnung der Ewigkeitsformel