Excel Linear Interpolation (Inhaltsverzeichnis)
- Was ist Interpolation?
- Interpolation mit Prognosefunktion in Excel
- Beispiele für lineare Interpolation in Excel
Was ist Interpolation?
In der Welt der Mathematik ist die Interpolation eine Methode zum Erstellen neuer Datenpunkte mit Hilfe bekannter Datenpunkte. Die Interpolation schätzt den Wert basierend auf den vorhandenen verfügbaren Datenwerten, die zuordenbar sind.
Zum Beispiel - Wenn wir ein Fahrrad mit 60 km / h fahren und ein bestimmtes Ziel in 1 Stunde erreichen und wenn wir mit 45 km / h fahren und ein bestimmtes Ziel in 45 Minuten erreichen. Wie viel Zeit wird es also dauern, ein Ziel zu erreichen, wenn wir mit 30 km / h fahren.
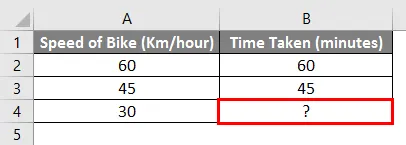
Mit einfacher Mathematik können wir die fehlenden Werte im obigen Beispiel berechnen. Wir müssen die folgende Formel in Zelle B4 einfügen.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
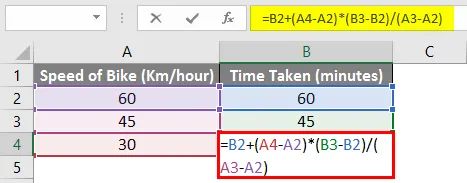
Auf der Grundlage der obigen Formel können wir also sagen, dass es 30 Minuten dauert, um das Ziel zu erreichen, wenn wir mit 30 km / h fahren.
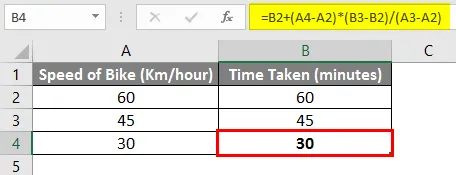
Versuchen wir, die obige Formel zu brechen und die Formel im Detail zu verstehen.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Im obigen Beispiel berechnet der letzte rot hervorgehobene Abschnitt der Formel, wie viel Zeit benötigt wird, wenn sich die Geschwindigkeit des Fahrrads um 1 ändert. In unserem Beispiel ändert sich die Zeit um 1 Minute, wenn sich die Geschwindigkeit des Fahrrads um 1 km ändert /Stunde.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Der zweite Abschnitt (oben in Blau) berechnet, wie weit unsere Fahrradgeschwindigkeit von der ersten angegebenen Fahrradgeschwindigkeit entfernt ist, und multipliziert diese mit dem oben berechneten Wert. Nach unserem Beispiel ist es 30 (Zelle A4) minus 60 (Zelle A2), dessen Ergebnis dann mit 1 multipliziert wird (was -30 entspricht).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Schließlich der erste Abschnitt der Formel (in Braun oben); Wir addieren den ersten Wert der Geschwindigkeit des Fahrrads. In unserem Beispiel ergibt dies das Endergebnis von 60 + (-30) * (1) = 30 Minuten. In der Schule haben wir die folgende Formel verwendet, um den fehlenden Wert von Y zu berechnen.
Y = Y1 + (X - X1) * (Y2 - Y1) / (X2 - X1)
Dies ist ein Beispiel für die Berechnung der fehlenden Werte mithilfe einer manuellen Formel zum Verständnis der Interpolation.
Excel hat eine eingebaute Funktion, die eine ähnliche Berechnung wie oben durchführt und als FORECAST-Funktion bezeichnet wird. Nun werden wir diese Funktion im Detail lernen.
Interpolation mit Prognosefunktion in Excel
Forecast ist eine Arbeitsblattfunktion, die in MS Excel verfügbar ist. Sie verwendet die lineare Regression, um den fehlenden Wert zu ermitteln. Prognose Wie der Name schon sagt, wird sie verwendet, um den zukünftigen Wert eines Datenpunkts vorherzusagen. Sie kann jedoch auch zum Interpolieren eines Werts verwendet werden. Grundsätzlich wird es verwendet, um den zukünftigen Wert basierend auf den vorhandenen Werten eines bestimmten Datensatzes zu berechnen.
Syntax der Prognosefunktion

Argumente der Prognosefunktion:
- x - Es ist ein Datenpunkt, für den wir den resultierenden Wert wissen wollen.
- Known_y’s - Zellbereich, der die Werte von Y enthält.
- Bekannte_x - Zellbereich, der die Werte von X enthält.
Lassen Sie uns nun anhand des obigen Beispiels versuchen, die Prognosefunktion zu verwenden.
In unserem Beispiel
x - Zelle B4 (wie wir die Zeit ermitteln wollen, die bei einer Geschwindigkeit von 30 km / h benötigt wird).
Known_y's - Zelle B2 bis Zelle B3 (Zeit, die für die bekannte Geschwindigkeit des Fahrrads benötigt wird).
Bekannte_x - Zelle A2 bis Zelle A3 (Geschwindigkeit des Fahrrads, für das wir die benötigte Zeit kennen).
Die endgültige Formel in Zelle B4 lautet also wie folgt:
= PROGNOSE (A4, B2: B3, A2: A3)
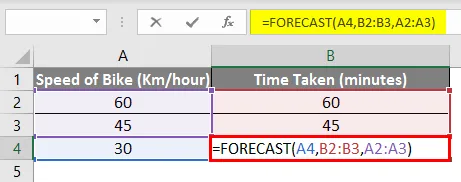
Und wie Sie sehen können, ist das Endergebnis das gleiche, dh 30 Minuten .
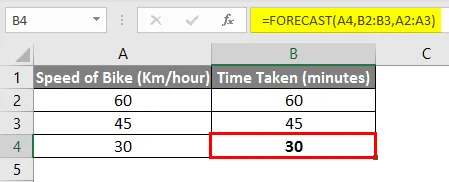
Um ein Diagramm zu erstellen, klicken Sie im Menü Einfügen auf Streuung und wählen Sie dann Streuung mit glatten Linien und Markierungen.
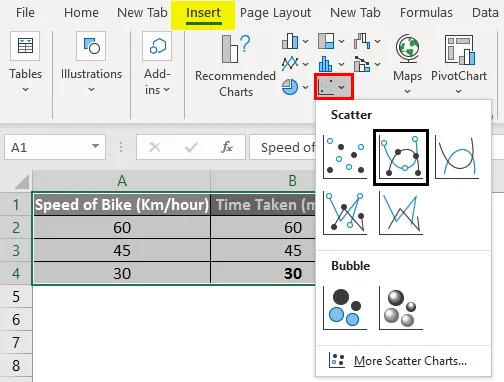
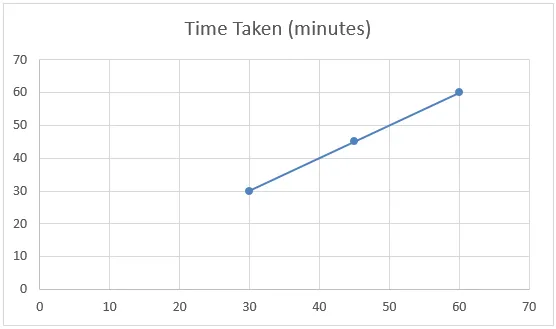
Wenn wir uns das folgende Diagramm des obigen Beispiels ansehen, können wir sagen, dass der Datensatz eine lineare Beziehung hat und als lineare Interpolation bezeichnet wird.
Beispiele für lineare Interpolation in Excel
Lassen Sie uns die lineare Interpolation in Excel anhand einiger Beispiele verstehen.
Sie können diese Excel-Vorlage für lineare Interpolation hier herunterladen - Excel-Vorlage für lineare InterpolationBeispiel 1
Angenommen, Sie haben Umsatz- und Gewinndaten für frühere Jahre und möchten den Gewinn des aktuellen Jahres erfahren, wenn Sie ein bestimmtes Umsatzniveau erreichen.
Schauen Sie sich die folgende Tabelle an. Sie haben Verkaufsdaten von 2016 bis 2018 und möchten wissen, was der Gewinn sein soll, wenn Ihre Verkäufe Rs sind. 40.000 im Jahr 2019.
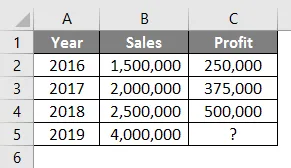
Mit Hilfe der Prognosefunktion können wir also den Gewinn von 2019 interpolieren, wenn der Umsatz Rs beträgt. 4.000.000
Die Formel in Zelle C5 lautet wie folgt:
= PROGNOSE (B5, C2: C4, B2: B4)
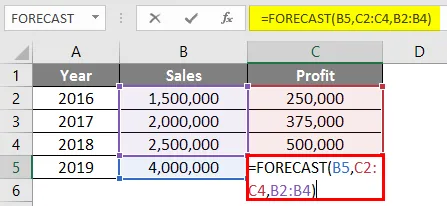
Nach Verwendung der Prognoseformel wird die unten stehende Antwort angezeigt.
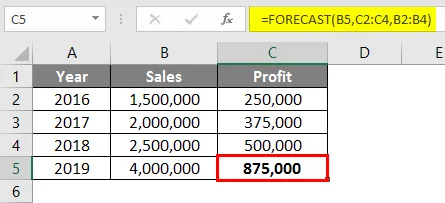
Das Ergebnis für die Prognosefunktion ist Rs. 875.000 basierend auf den von 2016 bis 2018 verfügbaren Umsatz- und Gewinndaten.
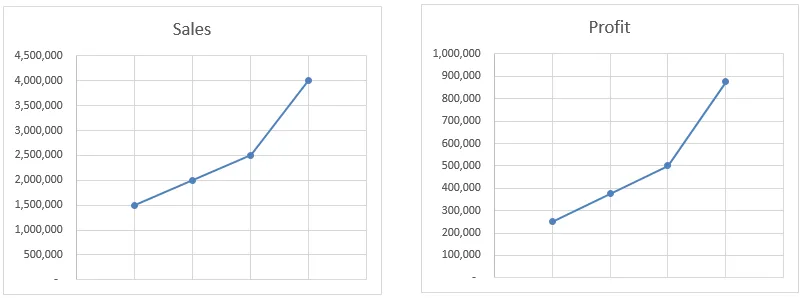
In diesem Beispiel interpoliert die Prognosefunktion den Wert basierend auf allen verfügbaren Daten und nicht nur auf Start- und Endpunkt. Wie Sie in den Diagrammen sehen können, bewegt sich der Gewinn genauso wie der Umsatz. Selbst wenn wir den Wert manuell berechnen, erhalten wir immer noch das gleiche Ergebnis.
Beispiel # 2
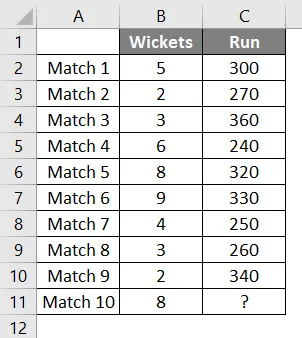
Wir haben Daten der letzten 9 Spiele der Cricketmannschaft, bei denen Wickets verschwunden sind und die von der Mannschaft gewertet wurden.
Wir wollen herausfinden, wie viele Läufe das Team erzielt, wenn 8 Pforten fallen.
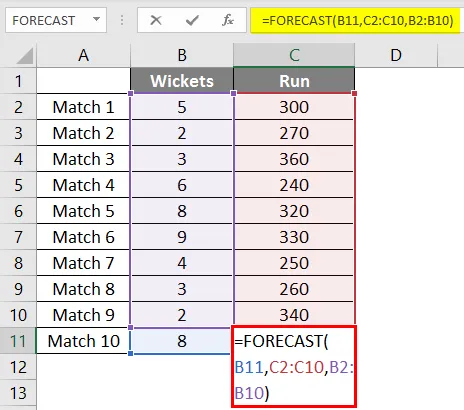
Wir werden also wieder dieselbe Prognosefunktion wie oben verwenden.
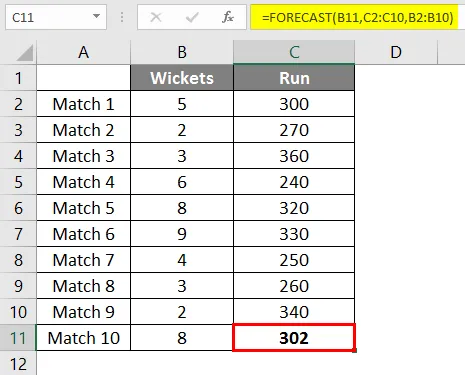
Nach Anwendung der Formel erhalten wir das Ergebnis von 302 Läufen, wenn 8 Pforten auf der Grundlage einer linearen Regression der letzten 9 vom Team gespielten Spiele fallen.
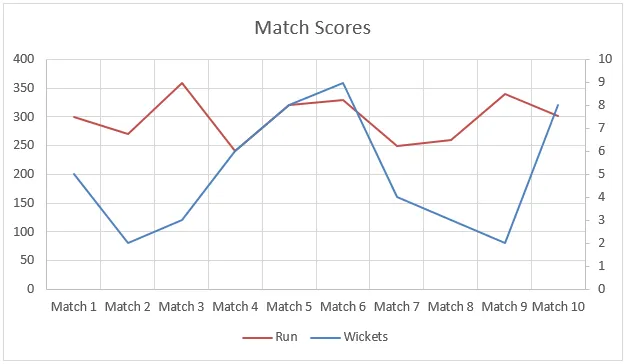
In diesem Beispiel waren die Daten nicht linear und Sie können dies in der folgenden Grafik sehen. Die Prognosefunktion hat uns jedoch dabei geholfen, die Läufe mithilfe von Daten früherer Spiele zu interpolieren.
Wichtige Informationen zur linearen Interpolation in Excel
- Die Prognosefunktion wird verwendet, um den Wert basierend auf den vorhandenen verfügbaren Werten vorherzusagen / zu schätzen, kann aber auch helfen, den fehlenden Wert zu interpolieren.
- Wenn die Daten nicht linear sind, erhalten Sie mit der Prognosefunktion nicht den genauen Wert, der auf der linearen Interpolation basiert, sondern den nächstgelegenen Wert.
- Wenn x in der Prognosefunktion Text oder nicht numerisch ist, gibt die Prognosefunktion den Fehler #WERT zurück.
- Wenn Known_x's und Known_y's keine Daten oder einen anderen Satz von Datenpunkten enthalten, gibt Forecast Function einen # N / A-Fehler aus.
- Wenn die Varianz von Known_x Null ist, gibt die Prognosefunktion den # DIV / O-Fehler aus.
Empfohlene Artikel
Dies ist eine Anleitung zur linearen Interpolation in Excel. Hier wird die Verwendung der linearen Interpolation in Excel zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage erläutert. Sie können auch unsere anderen Artikelvorschläge durchgehen -
- Lineare Regression in Excel
- Suchen Sie nach Text in Excel
- Textformel in Excel
- Marimekko Diagramm Excel
- In Excel interpolieren
- Lineare Programmierung in Excel