Einweg-Varianzanalyse
Die kurz als ANOVA geschriebene Varianzanalyse ist das Verfahren, mit dem wir Mittelwerte für drei oder mehr Populationen vergleichen können. Statistisch bilden wir zwei Hypothesen, die Nullhypothese: "Alle Populationsmittel sind gleich" und die Alternativhypothese: "Nicht alle Populationsmittel sind gleich". Es ermöglicht uns, die Gleichheit mehrerer Mittelwerte in einem Test zu testen, anstatt zwei Mittelwerte gleichzeitig zu vergleichen, was bei mehreren Gruppen nicht möglich ist. In diesem Thema lernen wir One Way ANOVA in R kennen.
Die einseitige Varianzanalyse hilft uns, nur einen Faktor oder eine Variable zu analysieren. ZB gibt es fünf Regionen und wir möchten überprüfen, ob die durchschnittlichen täglichen Niederschlagsmengen für alle fünf Regionen gleich oder unterschiedlich sind. In diesem Fall gibt es nur einen Faktor, nämlich die Region, da wir prüfen müssen, ob regionale Faktoren den Niederschlagsempfang und das Muster beeinflussen.
Annahmen der Varianzanalyse
Die folgenden Annahmen müssen für die Anwendung der Einweg-ANOVA erfüllt sein:
- Die Populationen, aus denen die Proben gezogen werden, sind normalverteilt.
- Die Populationen, aus denen die Proben entnommen wurden, haben die gleiche Varianz oder Standardabweichung.
- Die Stichproben aus verschiedenen Populationen sind zufällig und unabhängig.
Wie funktioniert One-Way-ANOVA in R?
Für unsere Demonstration verwenden wir die Daten, die zwei Variablen enthalten, nämlich. Marke und Vertrieb. Es gibt vier Marken - ATB, JKV, MKL und PRQ. Monatliche Verkäufe für diese Marken sind angegeben. Wir müssen prüfen, ob die durchschnittlichen Umsätze aller vier Marken gleich sind oder sich voneinander unterscheiden. Um dies zu überprüfen, verwenden wir die Einweg-ANOVA. Die schrittweise Vorgehensweise zum Implementieren von ANOVA lautet wie folgt:
- Importieren Sie zuerst die Daten in R. Die Daten liegen in einem CSV-Format vor. Um es zu importieren, verwenden wir die Funktion read.csv ().

- Zeigen Sie die ersten Datensätze der Daten an. Dies ist wichtig, um zu überprüfen, ob die Daten richtig in R importiert wurden. Ebenso werden wir eine summary () -Funktion auf die Daten anwenden, um grundlegende Einblicke in die Daten zu erhalten.

- Jedes Mal, wenn wir die im Datensatz vorhandenen Variablen verwenden, müssen wir den Namen des Datensatzes explizit erwähnen, z. B. brand_sales_data $ Brand oder brand_sales_data $ Sales. Um dies zu überwinden, werden wir die Attach-Funktion verwenden. Die Funktion muss wie folgt angewendet werden.

- Lassen Sie uns Verkäufe nach Marke mit Mittelwert oder Standardabweichung aggregieren. Durch die Aggregation erhalten wir eine grundlegende Vorstellung von Daten.
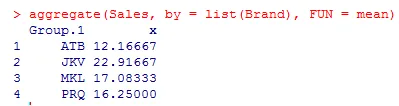
Das obige Ergebnis zeigt, dass die Mittelwerte für die vier verschiedenen Gruppen nicht gleich sind. JKV hat den höchsten Durchschnittsumsatz.
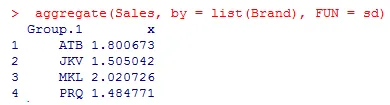
Wie oben zu sehen ist, zeigen die Standardabweichungen zwischen den vier Gruppen keinen signifikanten Unterschied und sind für die Marke MKL am höchsten.
- Nun wenden wir ANOVA an, um zu überprüfen, ob die Mittelwerte für die drei Populationen gleich sind oder ob ein Unterschied besteht.
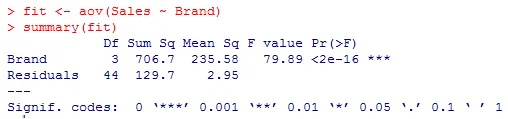
Aus den obigen Ergebnissen können wir erkennen, dass der ANOVA-Test für Brand aufgrund von p <0, 0001 signifikant ist. Wir können interpretieren, dass nicht alle Marken die gleichen Präferenzen auf dem Markt haben, was den Verkauf dieser Marken auf dem Markt beeinflusst. Dies könnte auf viele Faktoren und die Vorliebe der Menschen für eine bestimmte Marke zurückzuführen sein.
- Das obige Ergebnis kann visualisiert werden und erleichtert die Interpretation. Dafür verwenden wir die Funktion plotmeans () in der Bibliothek gplots (). Es funktioniert wie folgt:

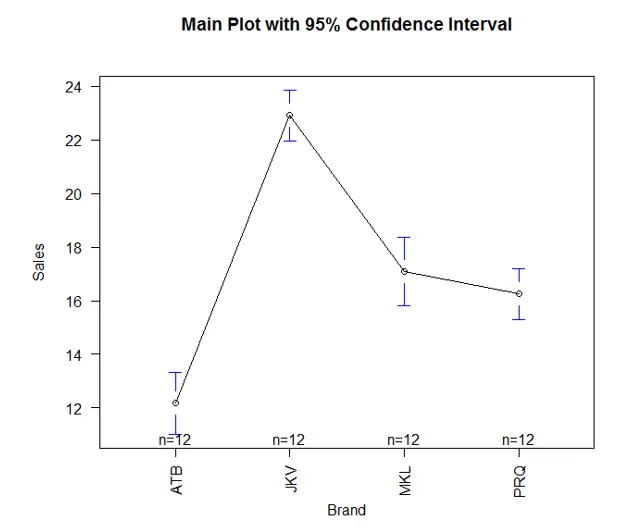
Wie wir oben sehen können, können wir mit der Funktion plotmeans () im Paket gplots die Mittelwerte verschiedener Gruppen visuell vergleichen. Wir können sehen, dass die Mittelwerte für alle vier Marken unterschiedlich sind. Die Mittel für die Marken MKL und PRQ liegen jedoch im engen Bereich.
- Die obige Analyse hilft uns zu überprüfen, ob Marken die gleichen Mittel haben oder nicht, jedoch ist der paarweise Vergleich damit schwierig. Mit der TukeyHSD () - Funktion können wir paarweise Vergleiche für verschiedene Marken anstellen, um festzustellen, ob sich eine Marke erheblich von den übrigen unterscheidet.

Die paarweisen Vergleiche wie oben. Der Unterschied zwischen zwei Gruppen ist signifikant, wenn p <0, 001 ist. Wie wir oben sehen können, ist der p-Wert für das PRQ-MKL-Paar viel höher, was darauf hinweist, dass sich die beiden Marken nicht signifikant voneinander unterscheiden.
Um die paarweisen Vergleiche zu visualisieren, zeichnen wir die obigen Ergebnisse wie folgt auf:

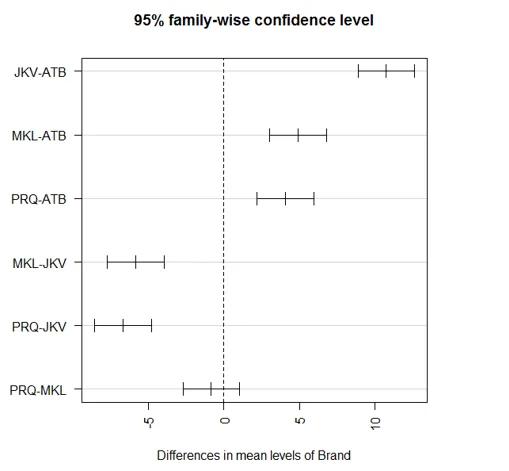
Die erste Par-Funktion dreht die Achsenbeschriftungen, sodass sie horizontal sind, und die zweite Par-Anweisung passt die Ränder so an, dass die Beschriftungen richtig passen. Andernfalls werden sie aus dem Bildschirm ausgeblendet.
Die obige Grafik bietet gute Einblicke, aber wir können die Ergebnisse in Form eines Boxplots darstellen, um bessere Einblicke für eine klarere Interpretation zu erhalten, wie unten gezeigt.

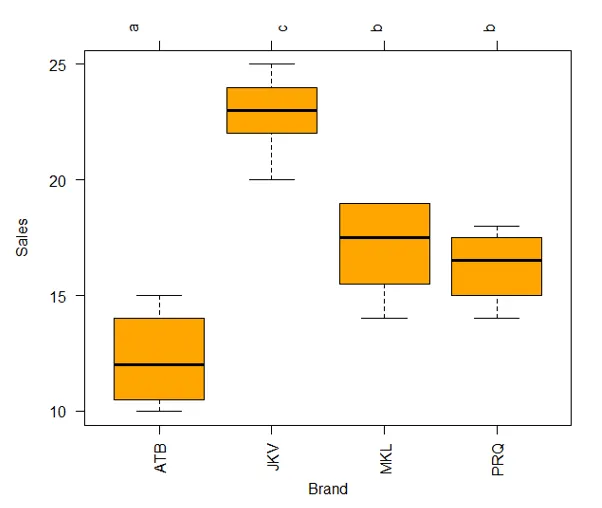
Die oben verwendete Funktion glht () enthält eine umfassende Reihe von Methoden zum Vergleichen mehrerer Mittelwerte. Beachten Sie, dass sich die Level-Option in der Funktion cld () auf das Signifikanzlevel bezieht, z. B. 0, 05 oder 95 Prozent Konfidenz.
Mit der obigen Darstellung wird es einfach, die Mittelwerte zwischen den Gruppen zu vergleichen, und es wird auch die systematische Interpretation erleichtert. Über dem Grundstück befinden sich Buchstaben für jede Marke. Wenn zwei Marken den gleichen Buchstaben haben, haben sie keine signifikant unterschiedlichen Mittelwerte wie in diesem Fall die Marken MKL und PRQ, die den gleichen Buchstaben haben. B.
- Bisher haben wir ANOVA implementiert und Diagramme verwendet, um die Ergebnisse zu visualisieren. Es ist jedoch ebenso wichtig, die Annahmen zu testen. Zunächst werden wir die Normalitätsannahme validieren.

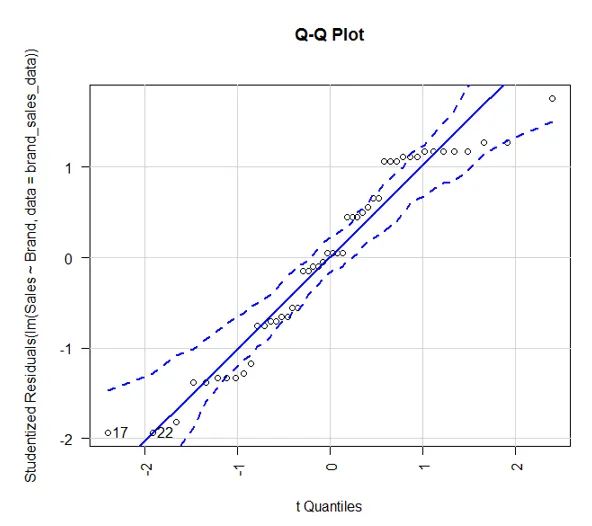
Das Autopaket in R bietet die Funktion qqPlot (). Die obige Darstellung zeigt, dass die Daten innerhalb eines Konfidenzbereichs von 95% liegen. Dies zeigt an, dass die Normalitätsannahme fast erfüllt ist.
Als nächstes werden wir prüfen, ob die Abweichungen zwischen den Marken gleich sind. Dazu verwenden wir den Bartlett-Test
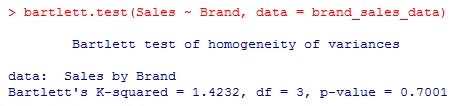
Der p-Wert zeigt, dass sich die Varianzen innerhalb der Gruppe nicht signifikant unterscheiden
Last but not least werden wir prüfen, ob es Ausreißer gibt, die die ANOVA-Ergebnisse beeinflussen.
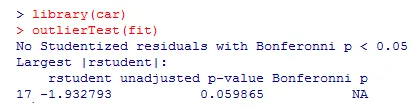
Anhand des obigen Ergebnisses können wir erkennen, dass die Daten keinen Hinweis auf Ausreißer enthalten (NA tritt auf, wenn p> 1 ist).
Unter Berücksichtigung der Ergebnisse von QQ Plot, Bartletts Test und Outlier-Test können wir sagen, dass die Daten alle ANOVA-Annahmen erfüllen und die erhaltenen Ergebnisse gültig sind.
Fazit - Einweg-ANOVA in R
ANOVA ist eine sehr praktische statistische Technik, mit der Mittelwerte über mehrere Populationen hinweg verglichen werden können. R bietet eine umfassende Palette von Paketen zur Implementierung von ANOVA, zur Ableitung von Ergebnissen und zur Validierung der Annahmen. In R können statistische Ergebnisse in visuellen Formen interpretiert werden, die tiefere Einblicke bieten.
Empfohlene Artikel
Dies ist eine Anleitung zur Einweg-ANOVA in R. Hier werden die Funktionsweise der Einweg-ANOVA und die Annahmen der Varianzanalyse erläutert. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- R Programmiersprache
- Regression gegen ANOVA
- Interpretation der Ergebnisse mit dem ANOVA-Test
- GLM in R