
F-Testformel (Inhaltsverzeichnis)
- Formel
- Beispiele
Was ist F-Testformel?
Der F-Test ist ein statistischer Test, mit dem wir herausfinden können, ob zwei Populationsgruppen mit normaler Verteilung ihrer Datenpunkte die gleiche Standardabweichung oder Varianz aufweisen. Vor allem aber sollten die Datensätze eine Normalverteilung haben, um einen F-Test durchzuführen. Dies wird unter der Nullhypothese auf die F-Verteilung angewendet. Der F-Test ist ein sehr wichtiger Bestandteil der Varianzanalyse (ANOVA) und wird anhand von Verhältnissen zweier Varianzen zweier unterschiedlicher Datensätze berechnet. Wie wir wissen, geben Abweichungen Auskunft über die Streuung der Datenpunkte. Der F-Test wird auch in verschiedenen Tests wie der Regressionsanalyse, dem Chow-Test usw. verwendet.
Formel FÜR F-Test:
Es gibt keine einfache Formel für F-Test, aber es gibt eine Reihe von Schritten, die wir befolgen müssen:
Schritt 1: Um einen F-Test durchzuführen, müssen wir zuerst die Nullhypothese und die Alternativhypothese definieren. Diese sind gegeben durch:
- H0 (Nullhypothese): Varianz des 1. Datensatzes = Varianz eines 2. Datensatzes
- Ha: Varianz des 1. Datensatzes <Varianz des 2. Datensatzes (für einen unteren einseitigen Test)
- Ha: Varianz des 1. Datensatzes> Varianz eines 2. Datensatzes (für einen oberen einseitigen Test)
- Ha: Varianz des 1. Datensatzes ≠ Varianz eines 2. Datensatzes (für einen zweiseitigen Test)
Schritt 2: Als nächstes müssen wir das Signifikanzniveau herausfinden und dann die Freiheitsgrade sowohl des Zählers als auch des Nenners bestimmen. Dies hilft uns bei der Bestimmung ihrer kritischen Werte. Der Freiheitsgrad ist die Stichprobengröße -1.
Schritt 3: F-Testformel:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Schritt 4: Ermitteln Sie den kritischen F-Wert aus der F-Tabelle unter Berücksichtigung eines Freiheitsgrades und eines Signifikanzniveaus.
Schritt 5: Vergleichen Sie diese beiden Werte. Wenn ein kritischer Wert kleiner als der F-Wert ist, können Sie die Nullhypothese ablehnen.
Beispiele für F-Testformeln (mit Excel-Vorlage)
Nehmen wir ein Beispiel, um die Berechnung von F-Test besser zu verstehen.
Sie können diese Excel-Vorlage für F-TEST-Formeln hier herunterladen - Excel-Vorlage für F-TEST-FormelnF-Testformel - Beispiel # 1
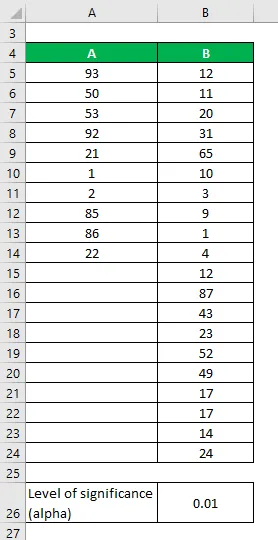
Angenommen, wir haben zwei Datensätze A und B, die unterschiedliche Datenpunkte enthalten. Führen Sie einen F-Test durch, um festzustellen, ob wir die Nullhypothese bei einem Signifikanzniveau von 1% ablehnen können.
Datensätze:
Lösung:
Nullhypothese: Varianz von A = Varianz von B
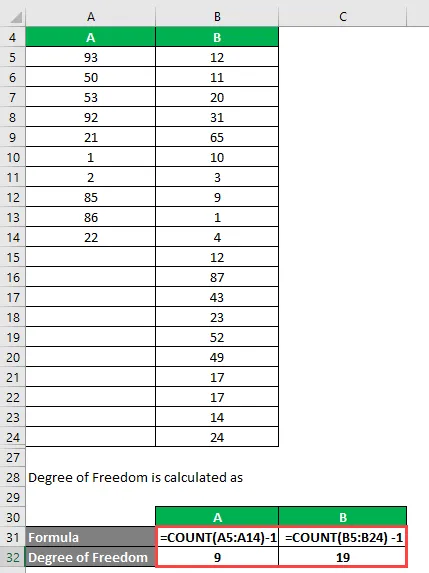
Freiheitsgrad wird berechnet als
Freiheitsgrad
- Für A = 10 - 1 = 9
- Für B = 20 - 1 = 19
Variation wird berechnet als:

- Varianz von A = 1385, 61
- Varianz von B = 521, 22
F Der Wert wird mit der unten angegebenen Formel berechnet
F Wert = Varianz des 1. Datensatzes / Varianz des 2. Datensatzes
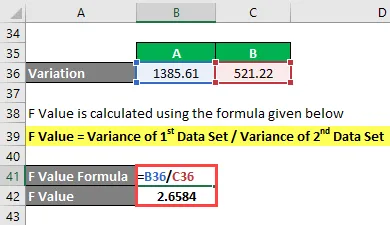
- F-Wert = 1385, 61 / 521, 22
- F-Wert = 2, 6584
F-Tabelle:
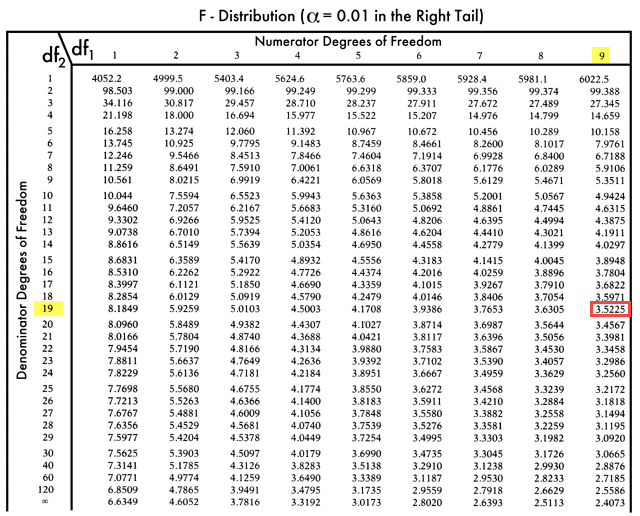
Also F kritischer Wert = 3, 5225
Da F critical größer als der F-Wert ist, können wir die Nullhypothese nicht ablehnen.
F-Testformel - Beispiel # 2
Angenommen, Sie arbeiten in einem Forschungsunternehmen und möchten wissen, wie hoch die Kohlendioxidemissionen von 2 verschiedenen Zigarettenmarken sind und ob sie sich erheblich voneinander unterscheiden oder nicht. In Ihrer Analyse haben Sie die folgenden Informationen gesammelt:
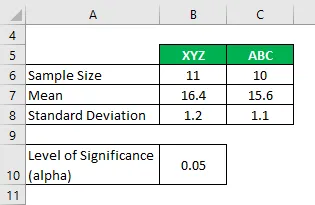
Lösung:
Freiheitsgrad wird berechnet als
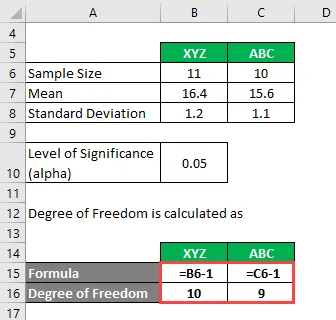
Freiheitsgrad
- Für XYZ = 11 - 1 = 10
- Für ABC = 10 - 1 = 9
Variation wird berechnet als:
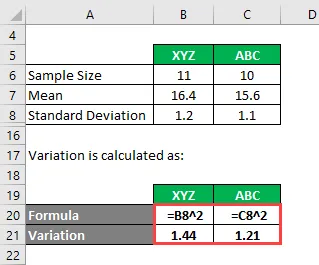
- Varianz von XYZ = 1, 2 2 = 1, 44
- Varianz von ABC = 1, 1 2 = 1, 21
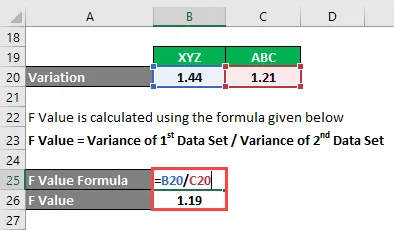
- F-Wert = 1, 44 / 1, 21
- F-Wert = 1, 19
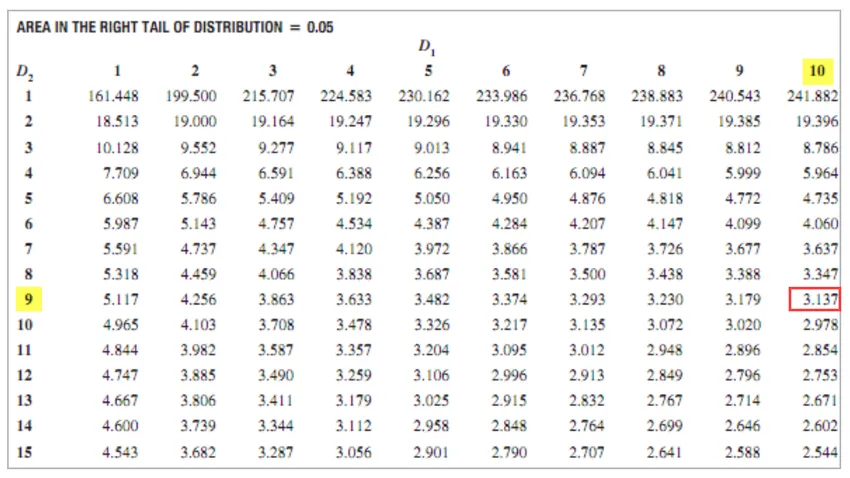
F kritischer Wert = 3, 137
Da der F-kritische Wert> F ist, kann die Nullhypothese nicht verworfen werden.
Erläuterung
In den obigen Beispielen haben wir die Anwendung von F-Test und dessen Durchführung gesehen. Es gibt jedoch eine Reihe von Annahmen, die wir berücksichtigen müssen, bevor wir den F-Test durchführen, da wir sonst nicht die erforderlichen Ergebnisse erhalten:
- Als erstes müssen wir immer den Zähler mit dem höheren Varianzwert platzieren, während wir den F-Wert berechnen. Wenn also F = V1 / V2 ist, sollte V1> V2 sein
- Wenn wir einen 2-Tail-Test durchführen möchten, müssen wir das Signifikanzniveau durch 2 dividieren, um den kritischen Wert zu ermitteln
- Wir verwenden nur die Varianz zur Berechnung des F-Werts. Wenn wir die Standardabweichungen wie in Beispiel 2 verwenden, müssen diese quadriert werden, um die Varianz zu ermitteln.
- Beide Proben sollten unabhängig voneinander sein und die Probengröße sollte unter 30 liegen
- Populationssets, aus denen die Stichproben gezogen werden, müssen normalverteilt sein
Dies sind die wichtigsten Parameter / Annahmen, die bei der Durchführung des F-Tests berücksichtigt werden sollten.
Relevanz und Verwendung der F-Testformel
F-Test hilft uns, wie oben erläutert, die Gleichheit der beiden Populationsvarianzen zu überprüfen. Wenn wir also zwei unabhängige Stichproben aus einer normalen Grundgesamtheit haben und prüfen möchten, ob sie die gleiche Variabilität aufweisen oder nicht, verwenden wir den F-Test. F-Test hat auch eine große Relevanz in der Regressionsanalyse und zum Testen der Signifikanz von R 2 . Kurz gesagt, F-Test ist ein sehr wichtiges Werkzeug in der Statistik, wenn wir die Variation von zwei oder mehr Datensätzen vergleichen möchten. Man sollte jedoch alle Annahmen im Auge behalten, bevor man diesen Test durchführt.
Empfohlene Artikel
Dies war ein Leitfaden für die F-Test-Formel. Hier besprechen wir die Berechnung des F-Tests zusammen mit praktischen Beispielen und einer herunterladbaren Excel-Vorlage. Sie können sich auch die folgenden Artikel ansehen, um mehr zu erfahren -
- T Verteilungsformel
- Formel für die Anleihenbewertung
- Prozentuale Fehlerformel
- Berechnung der NOPAT-Formel